对抗强化学习的光滑策略迭代（SPI）架构详解-优快云博客

本文链接：https://blog.youkuaiyun.com/kevin6liu6/article/details/147341256

众所周知， max算子（或者min算子）是贝尔曼方程的核心组件，它的高效求解贯穿了各类强化学习算法的始终，包括PPO、TRPO、DDPG、DSAC、DACER等主流的Actor-Critic（中文译作：“知行互动”）算法。熟悉算法设计的朋友或许存在一个疑问：为什么算法迭代过程总是求解max算子呢？存在不存在一种可能性，“不使用”max算子也能设计稳定收敛的强化学习算法呢？这就是今天为大家介绍光滑策略迭代（SPI，Smooth Policy Iteration）架构：第一类摆脱“max算子限制”的对抗强化学习算法。

对抗强化学习是提升场景泛化能力的重要手段[1]。这类问题通常建模为零和马尔可夫博弈，其核心是寻找纳什均衡策略—即主导策略和对抗策略均无法通过单方面改变策略来获得更好结果的状态。典型对抗贝尔曼方程（Bellman Equation）是：

其中， $π\pi$ 被称作主导策略， $μ\mu$ 被称作对抗策略。这是一个典型的非线性方程，方程之内存在两个算子，即max算子或min算子，解析解难以直接获得，策略迭代（Policy Iteration）是常见的一种数值求解方法[2]。根据max和min算子的求解先后顺序，现有迭代框架可分为同步策略迭代和异步策略迭代。前者通过计算主导策略 $π\pi$ 和对抗策略 $μ\mu$ 的联合值函数实施策略评估，并依托该值函数同步执行min和max优化[3]。后者首先求解max算子得到主导策略的最差（worst-case）值函数，再通过min算子优化该值函数以寻找更好的对抗策略 $π′\pi'$ 。已有研究表明：同步策略迭代的计算效率高，但是无收敛保障，且对初始值极为敏感，主要依赖人工调节学习率比例获取可用策略。异步策略迭代产生的值函数序列具备单调下降特征，可保证收敛至纳什均衡，但策略评估中贝尔曼算子迭代需精确计算max函数，导致求解效率异常低下。

为了解决这一难题，清华大学李升波教授课题组提出了一类全新的对抗强化学习求解算法，即光滑策略迭代（Smooth Policy Iteration，SPI）。该算法是以异步策略迭代框架为基础，利用光滑函数近似贝尔曼算子，通过取消max优化算子的数值计算极大降低了求解复杂度[4]。首先，该研究发现：用于策略评估的贝尔曼算子满足压缩映射性质以及保证值函数有序更新的策略提升定理是强化学习算法收敛性的核心保障。据此，提出了保障SPI收敛的三个基本条件：

近似算子的压缩映射性：用于保证策略评估的收敛性；
策略评估结果的可靠性：用于保证策略值函数的误差有界；
近似迭代框架的最优性：用于保证最优解为纳什均衡。

与此同时，该研究发现了首个符合上述收敛性条件的光滑近似函数，即Weighted Log-Sum-Exp（WLSE）函数。特别幸运的是该函数对于max算子的近似误差可显式求得，且具有连续可微和满足一阶Lipchitz条件的良好性质，表达式如下：

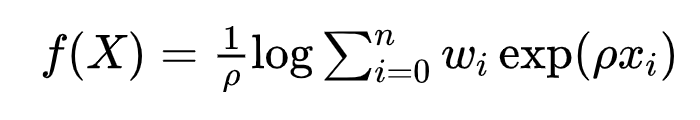
其中， $ρ\rho$ 为近似因子， $w_i$ 为满足归一性的权重。

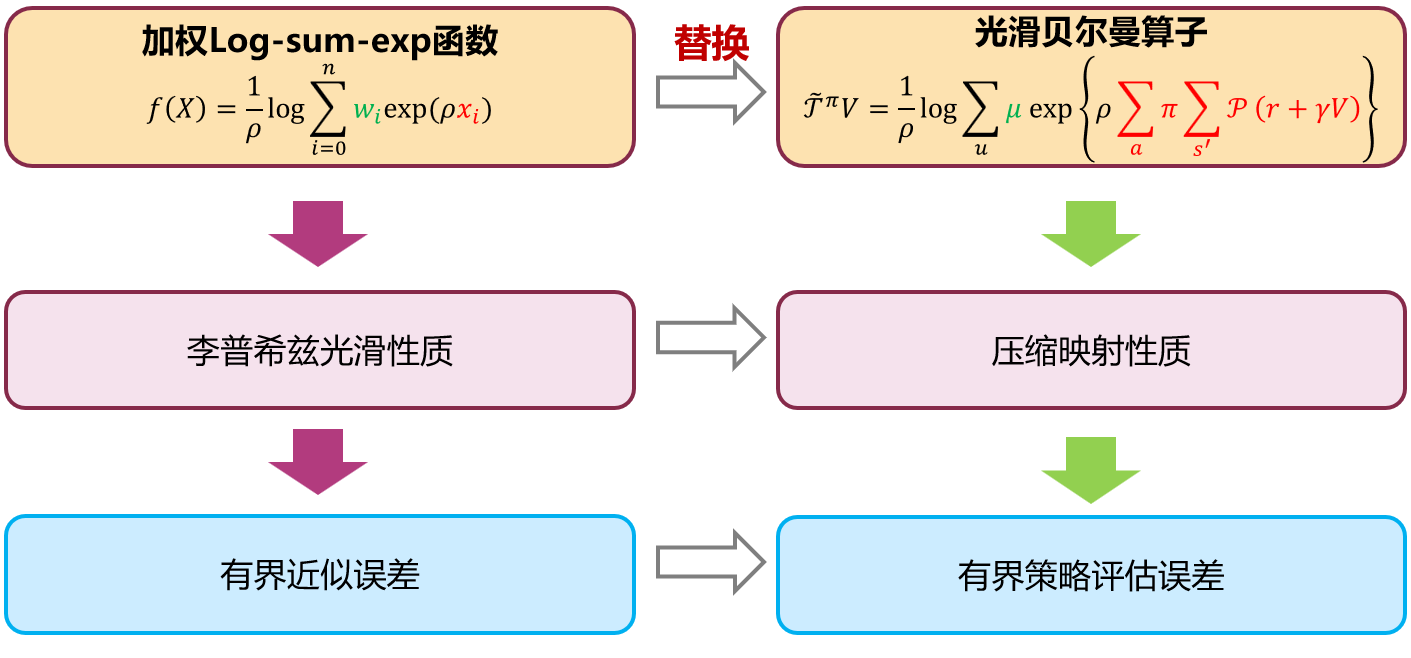
结合强化学习的特点，将贝尔曼算子中的max函数替换，构建了用于近似策略评估的光滑贝尔曼算子（见图1）。该算子以对抗策略作为加权函数，通过近似因子 $ρ\rho$ 实现值函数归一化。近似函数的Lipchitz性质可推导出光滑贝尔曼算子的压缩映射性质（符合收敛性条件1），意味着策略的近似值函数即为压缩映射的不动点。同时，根据近似函数的误差推导出光滑贝尔曼算子的有界误差（符合收敛性条件2），发现该误差与近似因子成线性反比，可通过调节近似因子实现对近似误差的控制。

图1 通过加权log-sum-exp函数构建光滑贝尔曼算子

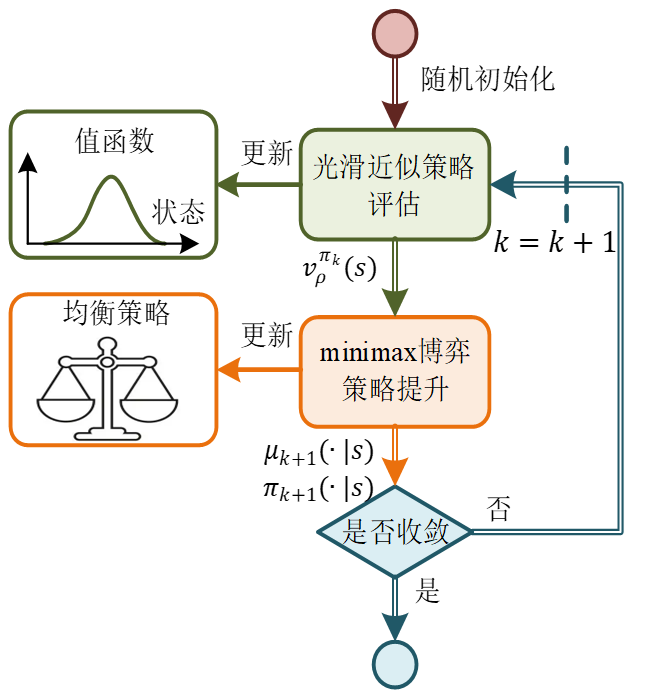
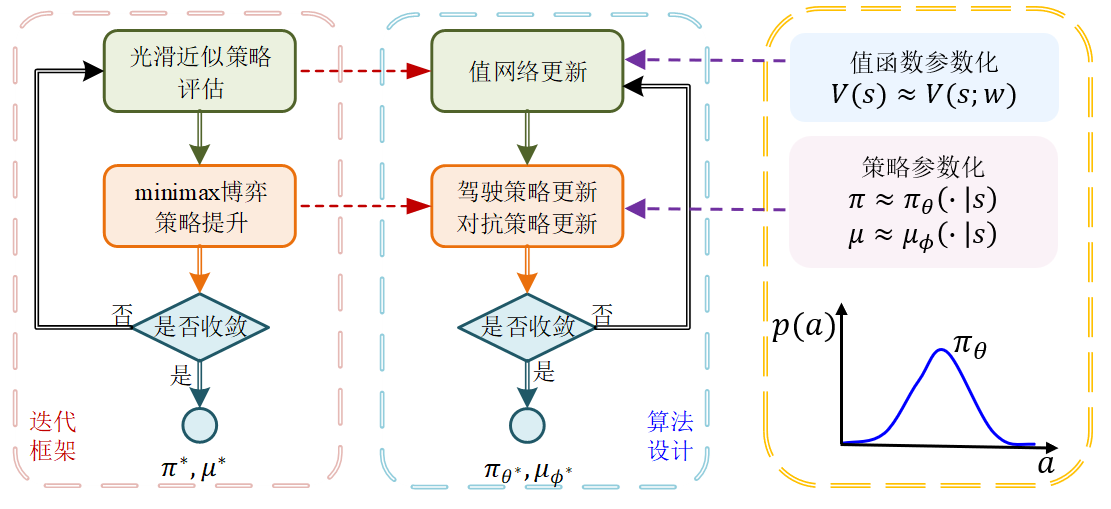
进一步，该研究将光滑贝尔曼算子用于策略评估的迭代求解过程，解决max优化带来的高求解复杂度难题。同时采用参考异步策略迭代引入基于近似值函数的策略提升，构建了高效求解贝尔曼方程的光滑策略迭代（Smooth Policy Iteration，SPI）框架，如图2所示。从任意初始策略开始，策略评估采用光滑贝尔曼算子执行不动点迭代，获得策略 $π\pi$ 的近似值函数；随后，策略提升通过构造关于近似值函数的优化问题求解获得更优策略 $π′\pi'$ 。经分析，当策略评估的近似误差为 $ε\varepsilon$ 时，相邻两次策略迭代产生的值函数满足：

这一理论表明：虽然SPI的值函数序列不具备严格的单调下降性质，但是存在的 $(γ+1)ε/(1−γ)(\gamma+1)\varepsilon/(1-\gamma)$ 的容许误差，所以当近似因子 $ρ\rho$ 足够大时，该误差趋近于0（即满足收敛条件3）。综上所述，只要迭代过程不断增加 $ρ\rho$ 的取值，其值函数序列呈现出单调下降的趋势，加之值函数的有界性，该序列最终会收敛至不动点，即为对抗贝尔曼方程的解。

图2 光滑策略迭代框架

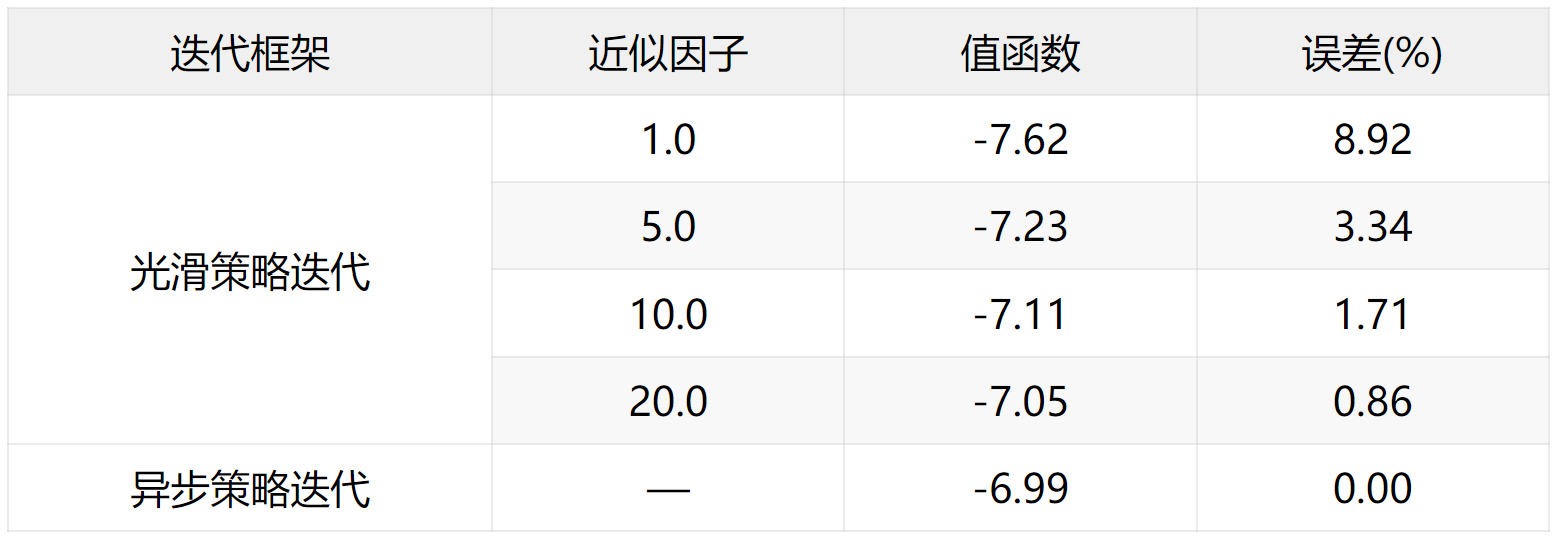
研究以经典的两状态零和马尔科夫博弈问题为例，对比SPI框架相对于异步策略迭代（API）架构求解纳什均衡的精度和效率。如表1所示, 不同近似因子的SPI和API策略值函数均收敛到固定值，说明迭代算子均具备压缩映射性质；而相对于API求得的值函数真值，近似因子 $ρ\rho$ 越大，SPI的近似值函数误差越小。进一步地，如果两种迭代框架均收敛到纳什均衡解，API需要14次迭代达到收敛，而SPI框架仅需10次迭代即可收敛，迭代次数下降了28.6%，且保持最优值函数近似误差小于1%。

表1 光滑策略迭代的近似误差

进一步地，研究以SPI框架为基础，引入神经网络作为策略载体，设计了用于求解鲁棒策略的深度强化学习算法，即Smooth Adversarial Actor-Critic（SAAC）。如图3所示，SAAC算法依照SPI框架的设计步骤，通过梯度优化进行值网络和策略网络的更新。值网络利用光滑贝尔曼算子构建目标值函数，其单调下降特性可引导值网络参数有序更新以缓解振荡，从而提升对抗训练的稳定性。策略网络基于值网络输出实现对抗策略$\mu$和主导策略$\pi$的同步更新，其性能指标为：

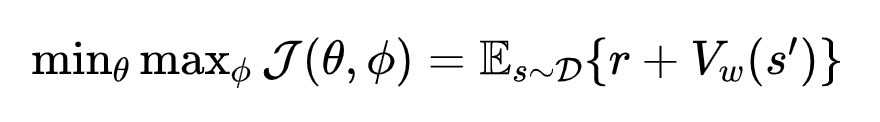
其中，主导策略采用梯度下降方式更新，对抗策略采用梯度上升方法更新。考虑对抗策略的边界对主导策略性能至关重要：边界过大会导致对抗策略干扰能力急剧增加，给主导策略带来强保守性。反之，偏移过小使对抗策略的探索空间有限，导致主导策略泛化能力提升不足。为此，研究设计了建立数据驱动的模型偏移边界选取方法，依托训练环境和应用环境的数据比对确定偏移范围，克服不合理偏移导致主导策略过于保守的不足。

图3 SPI框架与SAAC算法的对应关系

参考文献

[1] Ren Y, Duan J, Li S E, et al. Improving generalization of reinforcement learning with minimax distributional soft actor-critic[C]//23rd International Conference on Intelligent Transportation Systems. Rhodes, Greece: IEEE, 2020: 1-6.
[2] Li S E. Reinforcement learning for sequential decision and optimal control[M]. Singapore: Springer Verlag, 2023.
[3] Ren Y, Zhan G, Tang L, et al. Improve generalization of driving policy at signalized intersections with adversarial learning[J]. Transportation Research Part C: Emerging Technologies, 2023, 152: 104161.
[4] Ren Y, Lyu Y, Wang W, Li S E, et al. Smooth policy iteration for zero-sum Markov Games[J]. Neurocomputing, 2025, 630: 129666.