电子老鼠闯迷宫【BFS】

Description

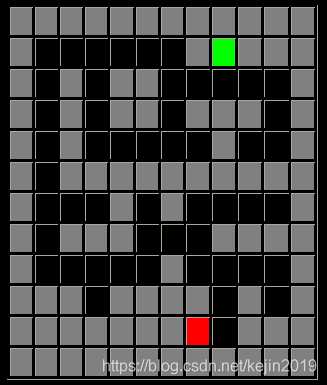
如下图$12\times 12$方格图，找出一条自入口$（2，9）$到出口$（11，8）$的最短路径。

---

Input
Output

---

Sample Input

12 //迷宫大小
2 9 11 8 //起点和终点
1 1 1 1 1 1 1 1 1 1 1 1 //邻接矩阵，0表示通，1表示不通
1 0 0 0 0 0 0 1 0 1 1 1
1 0 1 0 1 1 0 0 0 0 0 1
1 0 1 0 1 1 0 1 1 1 0 1
1 0 1 0 0 0 0 0 1 0 0 1
1 0 1 0 1 1 1 1 1 1 1 1
1 0 0 0 1 0 1 0 0 0 0 1
1 0 1 1 1 0 0 0 1 1 1 1
1 0 0 0 0 0 1 0 0 0 0 1
1 1 1 0 1 1 1 1 0 1 0 1
1 1 1 1 1 1 1 0 0 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1

Sample Output

(2,9)->(3,9)->(3,8)->(3,7)->(4,7)->(5,7)->(5,6)->(5,5)->(5,4)->(6,4)->(7,4)->(7,3)->(7,2)->(8,2)->(9,2)->(9,3)->(9,4)->(9,5)->(9,6)->(8,6)->(8,7)->(8,8)->(9,8)->(9,9)->(10,9)->(11,9)->(11,8)
27

---

解题思路

这一题用广搜解。。。作为一个刚学的蒟蒻，只会打板子
如果当前的位置可以走的话就tail加1，把当前位置的父结点加入队列；当现在的head（父结点）已经没有子结点的话，就把head加1，把上一个已经没有子结点的父结点退出队列。
只要是走过的路线都要把它赋值为1（障碍），防止有重复的路线，而且先到某一个路线的一定是最快最优的。

---

代码

#include<iostream>
#include<cstdio>
using namespace std;
const int dx[5]={0,0,0,1,-1};
const int dy[5]={0,1,-1,0,0};
int n,a,b,c,d,n1=0,bsy[200][200];//bsy为输入数组，也记录有没有走过
int st[200][3],fa[200];//st[][1]记录横坐标，st[][2]表示纵坐标，st[][3]记录步数，fa记录父节点
int h=0,t=1;
bool check(int x,int y)
{
	if(x>0&&x<=n&&y>0&&y<=n&&!bsy[x][y])//是否超界及有没有走过
	return 1;
	else
	return 0;
}
void out(int t){//递归输出
	if(t==1)
	return;
	out(fa[t]);
	printf("->(%d,%d)",st[t][1],st[t][2]);
}
void bfs(){
	fa[1]=0;
	st[1][1]=a;
	st[1][2]=b;
	st[1][3]=1;
	do{
		h++;
		for(int k=1;k<=4;k++)
		{
			if(check(st[h][1]+dx[k],st[h][2]+dy[k])){//判断是否符合
			   t++;
			   fa[t]=h;//储存父节点
			   st[t][1]=st[h][1]+dx[k];//储存位置
			   st[t][2]=st[h][2]+dy[k];//储存位置
			   st[t][3]=st[h][3]+1;//步数加1
			   bsy[st[t][1]][st[t][2]]=1;//标记已经走过该地
			   if(st[t][1]==c&&st[t][2]==d) //找到直接输出
			   {
			      cout<<"("<<a<<","<<b<<")";
			   	  out(t);
			      cout<<endl<<st[t][3];
			      h=21123;
			      t=0;
			      break;
			   }
			} 
		}
	}while(h<=t);
}
int main(){
	scanf("%d",&n);
	scanf("%d%d%d%d",&a,&b,&c,&d);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
			scanf("%d",&bsy[i][j]);
	}
	bfs(); 
}