【重学算法】红黑树

1. Red-Black Tree

红黑树，Red-Black Tree，是一种自平衡二叉查找树，被称为“对称二叉B树”。它可以在O（logn）时间内完成查找、插入和删除，这里的n是树中元素的数目。

红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：

(1) 根节点是黑色的；

(2) 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；

(3) 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；

(4) 从任一节点到其每个叶子的所有[简单路径]都包含相同数目的黑色节点。

这些约束确保了红黑树的关键特性：最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的。

 

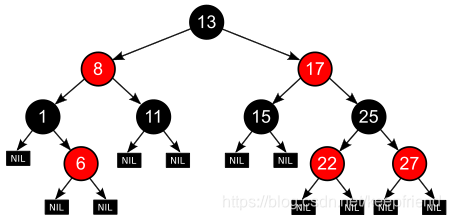
二叉查找树很多操作的性能都跟树的高度成正比。一棵极其平衡的二叉树（满二叉树或完全二叉树）的高度大约是 log2n，所以如果要证明红黑树是近似平衡的，我们只需要分析，红黑树的高度是否比较稳定地趋近 log2n 就好了。

如果我们将红色节点从红黑树中去掉，仅包含黑色节点的四叉树的高度，比包含相同节点个数的完全二叉树的高度还要小。完全二叉树的高度近似 log2n，这里的四叉“黑树”的高度要低于完全二叉树，所以去掉红色节点的“黑树”的高度也不会超过 log2n：