算法训练DAY2：LeetCode 209长度最小的子数组,59 螺旋矩阵，卡码网58区间和，44开发商买土地

LeetCode 209长度最小的子数组：

使用滑动窗口法，其实我觉得这个滑动窗口就是双指针法

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
       int result = INT_MAX;
       int fast=0,slow=0;
       int sum=0;
       for(fast;fast<nums.size();fast++)
       {
          sum +=nums[fast];
          while(sum>=target)
          {
            int sublength = fast-slow+1;//子串长
            result = min(result,sublength);//获得更小的子数组长度
            sum-=nums[slow++];
          }
         
       }
       return result==INT_MAX?0:result;
    }
};

让快指针先一直循环加下去，直到sum大于target的时候停下来，这时slow慢指针出动，一个一个减去sum[slow]直到sum再次小于target，fast再继续循环，最终就能获得最小的sublength

59.

画了个图（有点粗糙，主要是记录自己的思路和出现的问题）

首先确定转圈数：

然后模拟转一圈，思考需要哪些变量支撑：偏移量（用于让圈圈往内走），起始位置（用于定位，进行转圈操作）

代码：

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> result(n, vector<int>(n, 0)); // 定义二维数组
        int loop = n / 2;
        int mid = n / 2;
        int count = 1;              // 计数器
        int offset = 1;             // 初始偏移量
        int startx = 0, starty = 0; // 初始坐标
        int i, j;
        while (loop--) {
            // 从左往右
            for (i = startx, j = starty; j < n - offset; j++) {
                result[i][j] = count++;
            }//循环结束后j=n-offset
            // 从右往下
            for (i, j; i < n - offset; i++) {
                result[i][j] = count++;
            }
            // 从右往左
            for (i, j; j > starty; j--) {
                result[i][j] = count++;
            }
            // 从下往上
            for (i, j; i > startx; i--) {
                result[i][j] = count++;
            }
            offset += 1;
            startx += 1, starty += 1;
        }
        if (n % 2) {
            result[mid][mid] = count;
        }
        return result;
    }
};

中途遇到问题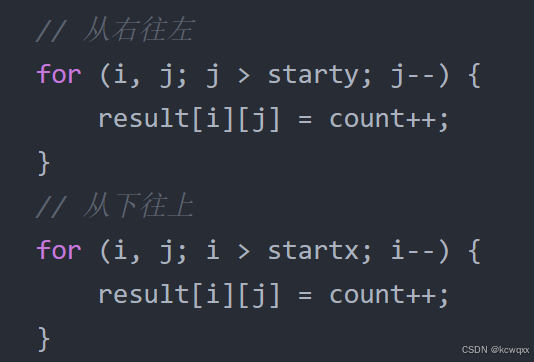： 为什么不取等？

画图解决：

以3*3矩阵为例，当j=1时， 进入下一次判断，j=1满足j>starty(此时为0）的条件，j--变成0，填入7

58.区间和

用前缀和解决：用数组vec记录元素值，数组pre记录一个又一个区间的值

算法时间复杂度始终为O(n),画图举例：

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    int n;
    cin>>n;
    vector<int>vec(n,0);
    vector<int>pre(n,0);
    int prehe=0;
    for(int i=0;i<n;i++)
    {
        cin>>vec[i];
        prehe+=vec[i];//用来帮助记录前缀和的值
        pre[i]=prehe;
    }
    int a=0,b=0,sum=0;
    while(~scanf("%d%d",&a,&b))
    {
        if(a==0)
        {
            sum=pre[b];  
        }
        else{
            sum=pre[b]-pre[a-1];
        }
        printf("%d\n",sum);  
    }
     return 0;
}

 意外收获：

把cin和cout改成scanf和printf可以大幅提高运行效率（以下是用时对比）

 44.开发商买土地

也可以使用前缀和来解题，思路如下：

代码：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;

int main()
{
    int n,m;
    cin>>n>>m;
    int sum=0;
    vector<vector<int>>nums(n,vector<int>(m,0));
    for(int i=0;i<n;i++)//行
    {
        for(int j=0;j<m;j++)//列
        {
            cin>>nums[i][j];
            sum+=nums[i][j];
        }
    }
    //记录横向
    vector<int>H(n,0);
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            H[i]+=nums[i][j];
        }
    }
    
    //记录纵向
    vector<int>V(m,0);
    for(int j=0;j<m;j++)
    {
        for(int i=0;i<n;i++)
        {
            V[j]+=nums[i][j];
        }
    }
    
    //求最小差值
    int  result=INT_MAX;
    int Hcut=0;
    for(int i=0;i<n;i++)
    {
        Hcut+=H[i];
        result=min(result,abs((sum-Hcut)-Hcut));
    }
    int Vcut=0;
    for(int j=0;j<m;j++)
    {
        Vcut+=V[j];
        result=min(result,abs((sum-Vcut)-Vcut));
    }
    
    
    printf("%d\n",result);
    return 0;
}