CH_8 Adaboost及其Spark实现_试用adaboost算法学习一个强分类器-优快云博客

本文链接：https://blog.youkuaiyun.com/k_wzzc/article/details/128909338

Adaboost是一种提升方法，通过结合多个弱分类器形成强分类器。它通过改变训练数据的权重，不断训练和优化，重点关注错误分类的样本。算法包括初始化权重，训练弱分类器，计算误差率，更新权重分布，以及构建分类器的线性组合。Adaboost例子展示了如何在不同轮次中调整权重并构建最终分类器。该算法优点在于能自适应调整样本权重，但可能对噪声敏感且迭代次数不易确定。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Adaboost

提升方法的基本思想

提升（boosting）方法是一种常用的统计学习方法，应用广泛且有效。在分类问题中，它通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能；对于一个复杂任务来说，将多个专家的判断进行适当的综合所得出的判断，要比其中任何一个专家单独的判断好。实际上，就是“三个臭皮匠顶个诸葛亮”的道理。

历史发展

历史上，Kearns和Valiant首先提出了”强可学习（strongly learnable）”和“弱可学习（weakly learnable）”的概念。他们指出：

在概率近似正确（probably approximately correct，PAC）学习框架中：

一个概念（一个类），如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么就称这个概念是强可学习的；
一个概念，如果存在一个多项式的学习算法能够学习它，学习的正确率仅比随机猜测略好，那么就称这个概念是弱可学习的。

boosting将一组弱学习器组合成一个强学习器，以最大限度地减少训练错误。在 boosting 中，随机选择数据样本，用模型拟合，然后按顺序进行训练——也就是说，每个模型都试图弥补其前身的弱点。在每次迭代中，来自每个单独分类器的弱规则被组合形成一个强预测规则。

boosting就是将一个 ”弱学习算法“ 提升为 “强学习方法”，最常见的算法包括Adaboost、Gradient boosting（GBDT）、XGBosst，本文将主要介绍Adaboost的算法原理及其实现。

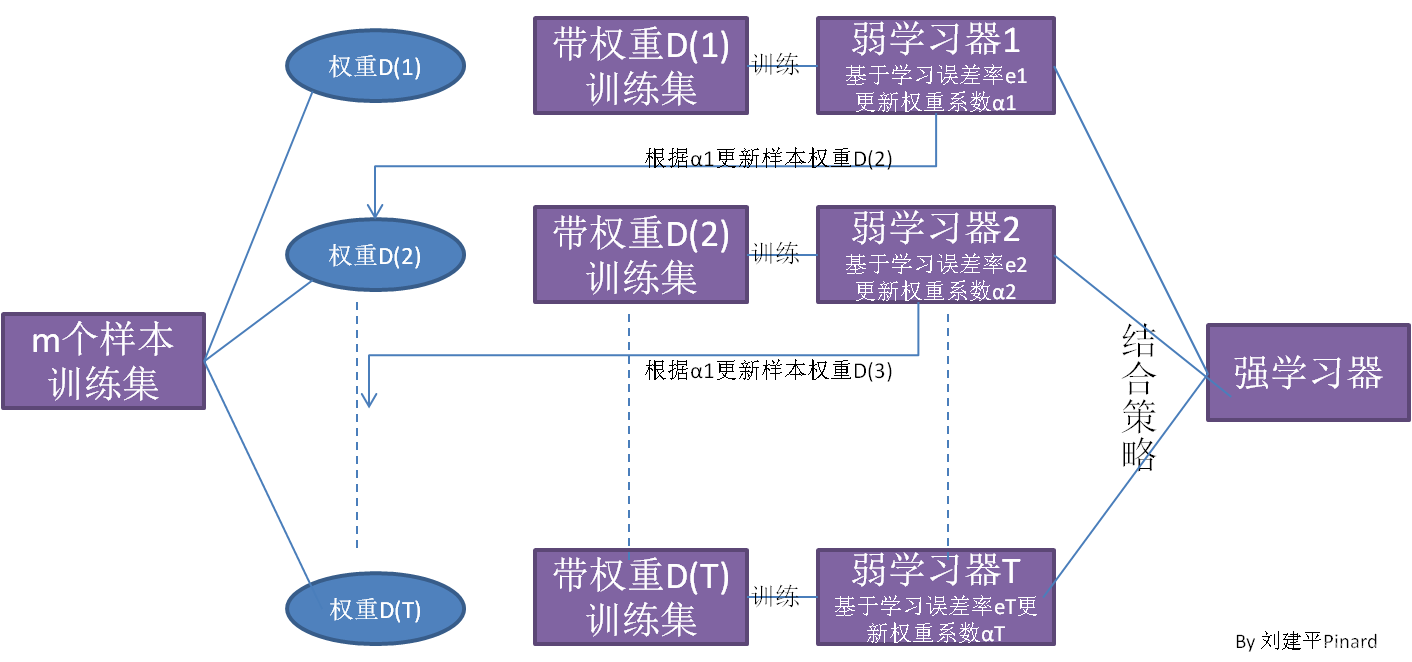
在这里插入图片描述

Adaboost

对提升方法来说，有两个问题需要回答：一是在每一轮如何改变训练数据的权值或概率分布；二是如何将弱分类器组合成一个强分类器。关于第1个问题，AdaBoost的做法是，提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值。这样一来，那些没有得到正确分类的数据，由于其权值的加大而受到后一轮的弱分类器的更大关注。于是，分类问题被一系列的弱分类器“分而治之”。至于第2个问题，即弱分类器的组合，AdaBoost采取加权多数表决的方法。具体地，加大分类误差率小的弱分类器的权值，使其在表决中起较大的作用；减小分类误差率大的弱分类器的权值，使其在表决中起较小的作用。

算法步骤

初始化数据权重
$D_{1} = (w_{11},……,w_{1i},……,w_{1N}) , w_{1i} = 1/N , i=1,2……,N$
对 m = 1,2,……M

对具有权值分布D_{m} 的数据集进行学习训练，得到弱分类器 $G_{m} (x): X->{-1,+1}$
计算Gm(x) 在训练集上的误分率 :
$\\e_{m} = \sum_{i=1}^N P(G_{m}(x) \not= y_{i}) = \sum_{i=1}^N w_{mi}I(G_{m}(Xi) \not= y_{i})$
计算Gm(x) 的α系数
$αm=1/2log[(1−em)em]\alpha_{m} = 1/2 log[\frac{(1-e_m) }{e_m}]$

当 em <= 1/2 时，α≥0，并且α随着e的减小而增大，所以mmm分类误差率越小的基本分类器在最终分类器中的作用越大。
更新训练数据集的权值分布:

$D_{m+1} = (w_{m+1,1},……w_{m+i,1},…… w_{m+1,N})$
$w_{m+1,i} = \frac{ w_{m,i}}{Z_{m}} e^{ -\alpha_{m} y_{i} G_{m}(x_{i}) } , i= 1,2……,N$

Zm是规范化因子

$Z_{m} = \sum_{i=1}^N w_{m,i}e^{w_{m,i} e^{-\alpha_{m} y_{i}G_{m}(x_{i}) }}$

它使D_{m+1} 成为一个概率分布

$w_{m+1,i} = \begin{cases} \frac{w_{m,i}}{Z_m}e^{-\alpha_{m}} , G_{m}(x_{i}) = y_{i}\\ \frac{w_{m,i}}{Z_m}e^{\alpha_{m}} , G_{m}(x_{i}) \not = y_{i}\\ \end{cases}$
1. 构造基本分类器的线性组合
$\sum_{m=1}^M \alpha_{m}G_{m}(x)$
1. 得到最终的分类器
$sign(\sum_{m=1}^M \alpha_{m}G_{m}(x))$

Adaboost的例子

给定训练数据。假设弱分类器由x<v或x>v产生，其阈值v使该分类器在训练数据集上分类误差率最低。试用AdaBoost算法学习一个强分类器。

初始化数据的权值分布

$D_{1} = (w_{1,1},……,w_{1,10}) , w_{1,i}=0.1$

对m=1，

(a).在权值分布为D_{1} 的数据集上，计算各个分割点的误分类率，计算得出，在x=2.5的时候，误分率最低，所以基本分类器为：

$G_{1}(x) = \begin{cases} 1 , x <2.5 \\ -1 , x >2.5 \end{cases}$

(b).计算基本分类器的误差率
有三个错误的分类点（7，8，9）
$G1分类器的误差率e1=P(G1(xi)≠yi)=0.3G_{1} 分类器的误差率 e_{1} = P(G_{1}(x_{i}) \not= y_{i}) = 0.3$

(c ).计算基本分类器的α系数
$\alpha = 1/2 log(\frac{1-e_{1}}{e_{1}}) = 0.4236$

(d).更新训练集的权值分布
$D_{2} = (w_{2,1},……,w_{2,10}) = (0.07142,0.07142,0.07142, 0.1666, 0.1666, 0.1666,0.07142,0.07142,0.07142,0.07142)$
$f_{1}(x) = 0.4236 * G_{1}(x)$
$此时的组合分类器为 G(x) = sign(f_{1}(x)) = sign( 0.4236 * G_{1}(x) )$
数据集在f1(x) 上有3个误分类点

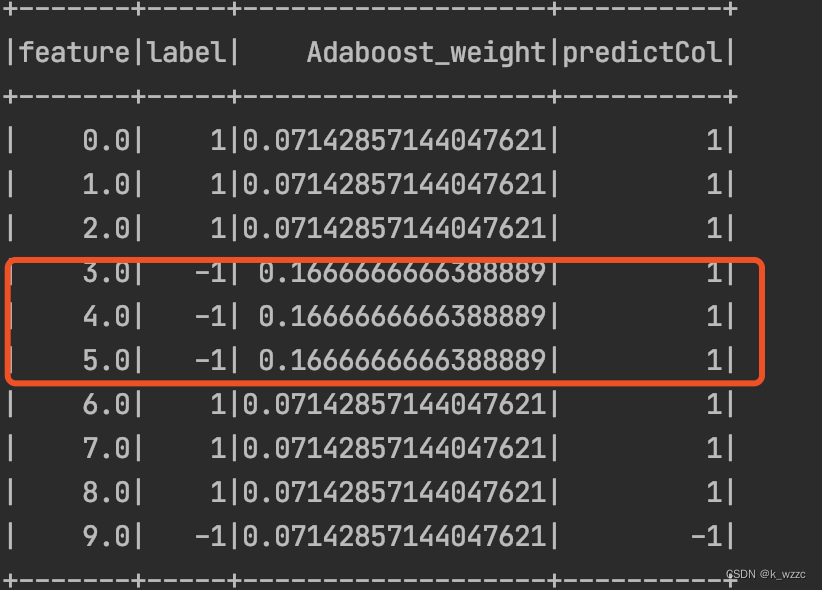
在这里插入图片描述

对m=2，

(a). 在权值分布为D_{2} 的数据集上，计算各个分割点的误分类率，计算得出，在x=8.5的时候，误分率最低，所以基本分类器为：

$G_{1}(x) = \begin{cases} 1 , x < 8.5 \\ -1 , x > 8.5 \end{cases}$

(b). 计算基本分类器的误差率）
$G2分类器的误差率e2=P(G2(xi)≠yi)=0.2143G_{2} 分类器的误差率 e_{2} = P(G_{2}(x_{i}) \not= y_{i}) = 0.2143$

(c ). 计算基本分类器的α系数
$\alpha = 1/2 log(\frac{1-e_{2}}{e_{2}}) = 0.6496$

(d) 更新训练集的权值分布
$D_{3} = (w_{3,1},……,w_{3,10}) = (0.04545,0.04545,0.04545,0.1060,0.1060,0.1060,0.1666,0.1666,0.1666,0.04545)$
$f_{2}(x) = 0.4236 * G_{1}(x) + 0.6496 * G_{2}(x)$
$此时的组合分类器为 G(x) = sign(f_{2}(x)) = sign( 0.4236 * G_{1}(x) + 0.6496 * G_{2}(x) )$
数据集在f2(x) 上有3个误分类点

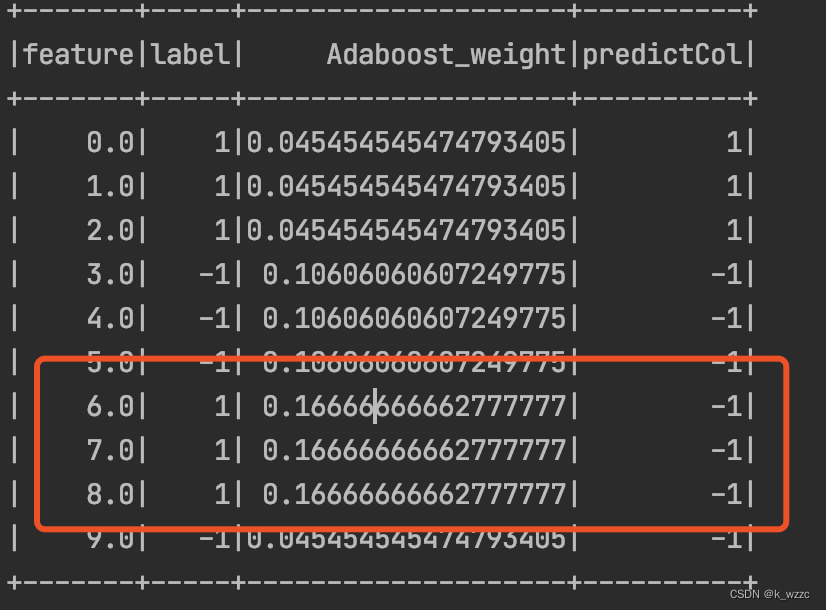
在这里插入图片描述

对m=3，

(a) 在权值分布为D_{3} 的数据集上，计算各个分割点的误分类率，计算得出，在x=5.5的时候，误分率最低，所以基本分类器为：

$G_{1}(x) = \begin{cases} 1 , x > 5.5 \\ -1 , x < 5.5 \end{cases}$

(b) 计算基本分类器的误差率）
$G3分类器的误差率e3=P(G3(xi)≠yi)=0.1820G_{3} 分类器的误差率 e_{3} = P(G_{3}(x_{i}) \not= y_{i}) = 0.1820$

(d) 更新训练集的权值分布
$D_{4} = (w_{4,1},……,w_{4,10}) = ()$
$f_{2}(x) = 0.4236 * G_{1}(x) + 0.6496 * G_{2}(x) + 0.7521 G_{3}(x)$
$此时的组合分类器为 G(x) = sign(f_{2}(x)) = sign( 0.4236 * G_{1}(x) + 0.6496 * G_{2}(x) + 0.7521 G_{3}(x) )$
数据集在f3(x) 上已经有100%的准确率，可以停止迭代。

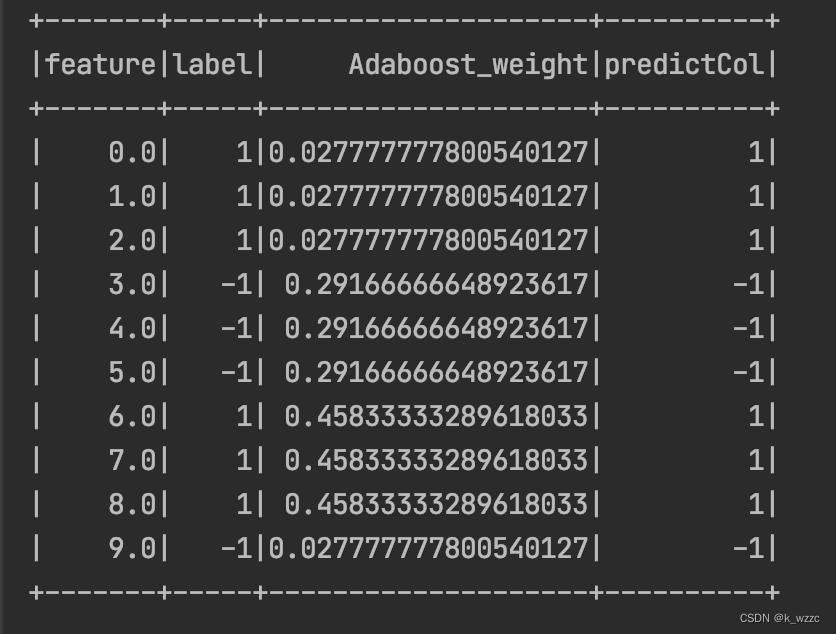
在这里插入图片描述

Adaboost算法的优缺点

优点：

（1）Adaboost提供一种框架，在框架内可以使用各种方法构建子分类器。可以使用简单的弱分类器，一般不容易过拟合。
（2）Adaboost算法最后得到的强分类器的分类精度依赖于所有弱分类器。
（3）Adaboost可以根据弱分类器的反馈，自适应地调整样本权重。
（4）相对于Bagging算法和Random Forest算法，Adaboost充分考虑每个分类器的权重。

缺点：

（1）Adaboost迭代次数也就是弱分类器数目不太好设定。
（2）Adaboost在训练中会偏向分类错误的样本，导致Adaboost算法易受噪声干扰。
（3）Adaboost在训练弱分类器时比较耗时，每次都要重新选择当前分类器最好切分点。

代码实现

// 决策树桩
case class DecisionStump(
                         ftsName: String, // feature name 特征
                         threshold: Double, // 阈值
                         polarity: Int, // 方向
                         alpham: Double, //
                         em: Double //
                       ) extends Serializable {


}

package CH8_Adaboost

import org.apache.spark.sql.expressions.UserDefinedFunction
import org.apache.spark.sql.{DataFrame, Row, SparkSession}
import org.apache.spark.sql.functions._
import org.apache.spark.sql.types.IntegerType
import scala.collection.mutable.ListBuffer


object Adaboost {
  def main(args: Array[String]): Unit = {

    val spark = SparkSession
      .builder()
      .appName(s"${this.getClass.getSimpleName}")
      .master("local[*]")
      .getOrCreate()

    import spark.implicits._

    spark.sparkContext.setLogLevel("ERROR")

    val dataInit = spark.read
      .format("csv")
      .option("inferSchema", true)
      .option("header", true)
      .load("/Users/wzzc/IdeaProjects/tdw_spark_mock_toolkit/src/main/resources/data/boosting.csv")
    //              .load("/Users/wzzc/IdeaProjects/tdw_spark_mock_toolkit/src/main/resources/data/iris.csv")
    //              .select("label", "sepalWidth", "sepalLength")

    dataInit.cache()


    //   权值更新
    def weightUpdateFunction(threshold: Double, alpha: Double, zm: Double): UserDefinedFunction =
      udf((x: Double, y: Int, w: Double) => {
        val gmi = if (x <= threshold) 1 else -1
        (w / zm) * math.exp(-alpha * y * gmi)
      })


    //    样本数
    val N = dataInit.count()
    //  标签
    val labelCol = "label"
    //  特征
    val features = dataInit.columns.filter(_ != labelCol)
    //  权重字段
    val weightName = "Adaboost_weight"
    // 初始化权重
    var data = dataInit.withColumn(weightName, lit(1.0 / N))

    val inteL: Int = 5 // 最大迭代次数
    val tol = 1e-2
    var convergence = true //判断收敛

    var i = 1
    val stumps = new ListBuffer[DecisionStump]()

    while (inteL >= i && convergence) {

      // 训练弱分类器，根据最小分类误差率选择最优划分特征,误分率,α系数
      val (ftsName, threshold, pol, alpham, em) = features.map(f => {
        //  计算最优分割点
        val thresholds = data
          .select(col(f)).distinct().map(_.getAs[Double](0))
          .collect()

        //  将每一个特征值作为分类阈值
        val (em, pol, threshold): (Double, Int, Double) = thresholds.map(threshold => {
          // 选择误分率最低(或者最高)的特征值
          var err: Double = data.select(col(f), col(labelCol), col(weightName))
            .rdd
            .map(r => {
              val xi = r.getAs[Double](0)
              val yi = r.getAs[Int](1)
              val wi = r.getAs[Double](2)
              val p = if (xi <= threshold) 1 else -1 // 根据阈值判断是否正确
              val gxi = if (yi == p) 0 else 1
              val e = wi * gxi //
              e
            })
            .sum()

          var polarity = 1

          if (err > 0.5) {
            polarity = -1
            err = 1 - err
          }

          (err, polarity, threshold)

        })
          .minBy(_._1)

        //   计算模型alpha  + 1e-10 防止em为0
        val alpham: Double = 0.5 * math.log((1 - em) / (em + 1e-10))

        (f, threshold, pol, alpham, em)

      }).minBy(_._5)

      stumps.append(DecisionStump(ftsName, threshold, pol, alpham, em))


      //  规范化因子
      val Zm = data.select(ftsName, weightName, labelCol)
        .collect()
        .map(r => {
          val x = r.getAs[Double](ftsName)
          val w: Double = r.getAs[Double](weightName)
          val y = r.getAs[Int](labelCol)
          val gmi = if (x <= threshold) 1 else -1
          w * math.exp(-alpham * y * gmi * pol)
        }).sum

      // 权值更新
      data = data.withColumn(weightName, weightUpdateFunction(threshold, alpham, Zm)
      (col(ftsName), col(labelCol), col(weightName))
      )

      // 计算模型累计误差
      val predictDF: DataFrame = predict(data, stumps)
      predictDF.show()
 
      val modelErr: Double = predictDF.withColumn("err", expr("if(label == predictCol,0,1)"))
        .agg(avg("err").as("modelErr"))
        .head()
        .getAs[Double]("modelErr")


      println(s"第${i}次迭代的特征：" + ftsName)
      println(s"第${i}次迭代的特征阈值 ：" + threshold)
      println(s"第${i}次迭代的alpha： " + alpham)
      println(s"第${i}次迭代的em： " + em)
      println(s"第${i}次迭代的规范因子 ：" + Zm)
      println(s"第${i}次迭代后的误差率 ：" + modelErr)
      println("=======================")

      // 判断收敛 
      convergence = tol <= modelErr
      i += 1

    }

    stumps.foreach(x => println(x.toString))


    def predict(data: DataFrame, models: Seq[DecisionStump]) = {

      val structType = data.schema.add("predictCol", IntegerType)
      val resRDD = data.rdd.map(r => {

        val fxi: Double = models.map(m => {
          val alpham = m.alpham
          val threshold = m.threshold
          val ftsName = m.ftsName
          val polarity = m.polarity
          val xi = r.getAs[Double](ftsName)
          val gxi = if (xi <= threshold) 1 else -1

          alpham * gxi * polarity
        })
          .sum

        Row.merge(r, Row(if (fxi >= 0) 1 else -1))
      })

      spark.createDataFrame(resRDD, structType)

    }
  }
}