电动汽车充电站动态定价

智能电力交通系统中的边际充电站定价

摘要

我们考虑了通过电动汽车（EV）在电力系统与交通系统之间引入的耦合关系。我们设想，若干充电网络运营商将跟踪电动汽车的移动情况，以更准确地估计其电池充电需求。他们利用这些信息，更合理地决策如何参与电力批发市场，并设计边际零售电价，以减少充电站的等待时间和电力成本。为了建立这些决策和定价问题的模型，我们引入了一种网络流模型，该模型通过在交通网络中增加虚拟弧段，能够捕捉电动汽车群体随时间变化的出行和充电模式。

一、引言

电动汽车（EV）有助于提高燃油经济性，增加可再生能源在电网中的渗透率，并减少排放。在过去八年中，电动汽车电池成本下降了70%，美国的电动汽车充电站数量从2008年的不到500个增长到如今的16,000多个，增长了40倍[1]。目前我们在大幅增加交通系统中电动汽车数量方面面临的主要障碍是电动汽车充电站稀缺，以及缺乏将充电位分配给电动汽车的控制机制，这导致了续航焦虑以及部分公共充电站出现长队等候充电的现象[2]。如果没有控制机制来引导驾驶员在最佳时间和地点充电，我们预计会出现两个主要问题：1）需求与基础设施容量的不匹配可能导致部分充电站利用率低下，而在热门地点则出现排长队的现象；2）电网中供需不匹配可能导致价格飙升、不稳定以及馈线容量越限[3]。因此，已有大量研究致力于通过设计适当的电动汽车充电负荷需求管理方案来解决这些问题。相关文献可大致分为以下两大类进行讨论。

第一类研究在聚合层面管理电动汽车电力负荷，大多数先前的工作将特定充电站的电动汽车插电事件视为外生随机过程。例如，[4]–[6]中的作者考虑了控制机制，可在电动汽车于特定位置插电后，根据动态电价或通过聚合控制实现电池的最优充电。一些近期的研究考虑了电动汽车出行模式对电力负荷管理的影响。例如，[7]中的作者考虑了运营商跟踪大规模电动汽车车队的移动性及其能耗，并设计最优多周期车网互动策略。[8]中考虑了电动汽车的驾驶时间和模式，并研究了不同电价对充电量和充电时机的影响，同时考虑了因发电机启动成本带来的非线性特性。

第二类将电价视为给定条件，重点研究单个电动汽车驾驶员或电动汽车群体的最优路径问题，考虑因素包括充电所需时间、电池中存储的有限能量以及续航焦虑（例如，参见[9],[10]及其中关于单个电动汽车的参考文献）。在系统层面，[11]研究大量电动汽车的最优路径，以最小化电动汽车从出行起点到目的地所需的行驶和充电时间。

本文中，我们将这两类方法相结合，设计了考虑地理分布的充电站需求的电价机制，该需求由驾驶员个体在时间和空间上变化的出行模式及其经济决策所驱动。我们最初在[12],[13],中研究了这一问题，探讨了两个非营利交通与电力系统运营商如何在一个理想环境下协同合作，以考虑通过电动汽车在其系统之间引入的互联。[12],[13]所依赖的一些主要假设包括：电动汽车车主直接从系统运营商处购买电力（即不存在零售商），所有交通链路和充电站均可施加庇古税（例如通行费），以及出行需求是静态的且不随时间变化。在本文中，我们取消了所有这些假设。

我们设想，少数大型竞争者（例如特斯拉或 Chargepoint等公司）将为单个电动汽车提供联合导航与充电规划服务，并运营地理上分散的充电站网络。单个电动汽车将考虑运营商提供的关于充电站可用性、价格和行驶时间的信息，并据此做出成本最小化决策，以决定如何出行和充电。具体而言，在第二节中，我们提出交通系统的网络模型，该模型能够数学化地描述个体决策对不同位置充电器可用性以及电力系统中电力负荷的影响。在第三节中，我们讨论个体用户的决策问题，以及该问题如何决定充电站的拥堵模式。第四节讨论电力的传统定价机制，第五节讨论考虑电动汽车因素后充电站的电力批发和零售价格。

II. 时扩交通网络

电动汽车的电能消耗源于驾驶员的出行需求。为了捕捉这种依赖关系，我们需要能够反映途中时间成本和充电决策中的电费等因素影响的交通模型。

这里我们采用常见的方法，将交通网络建模为有向图 G=(V, A)。弧段集合 A表示主要道路或高速公路，而 V中的节点要么表示进出道路的出入口，要么表示驾驶员行程的近似起点或目的地。

每位客户会选择交通网络 G上从其起点（例如家）到目的地（例如工作地点）总成本最低（包括充电成本）的路径。这一问题此前已根据不同选择的成本结构被建模为多种最短路径问题[14]。影响电动汽车成本结构的一个主要约束条件是需要插电并接收电池充电。我们将充电站分为两类：1）I型——客户无需等待充电完成的充电站，例如家用或工作场所的充电站。在此类站点，假设充电可中断，并可安排在电价较低且电力更充足的时段进行；2）II型——客户需等待车辆充电完成的快速充电站。在此类站点，假设充电不可中断。此外，I型（分别地，II型）充电站的集合表示为 VI（分别地， VII）。

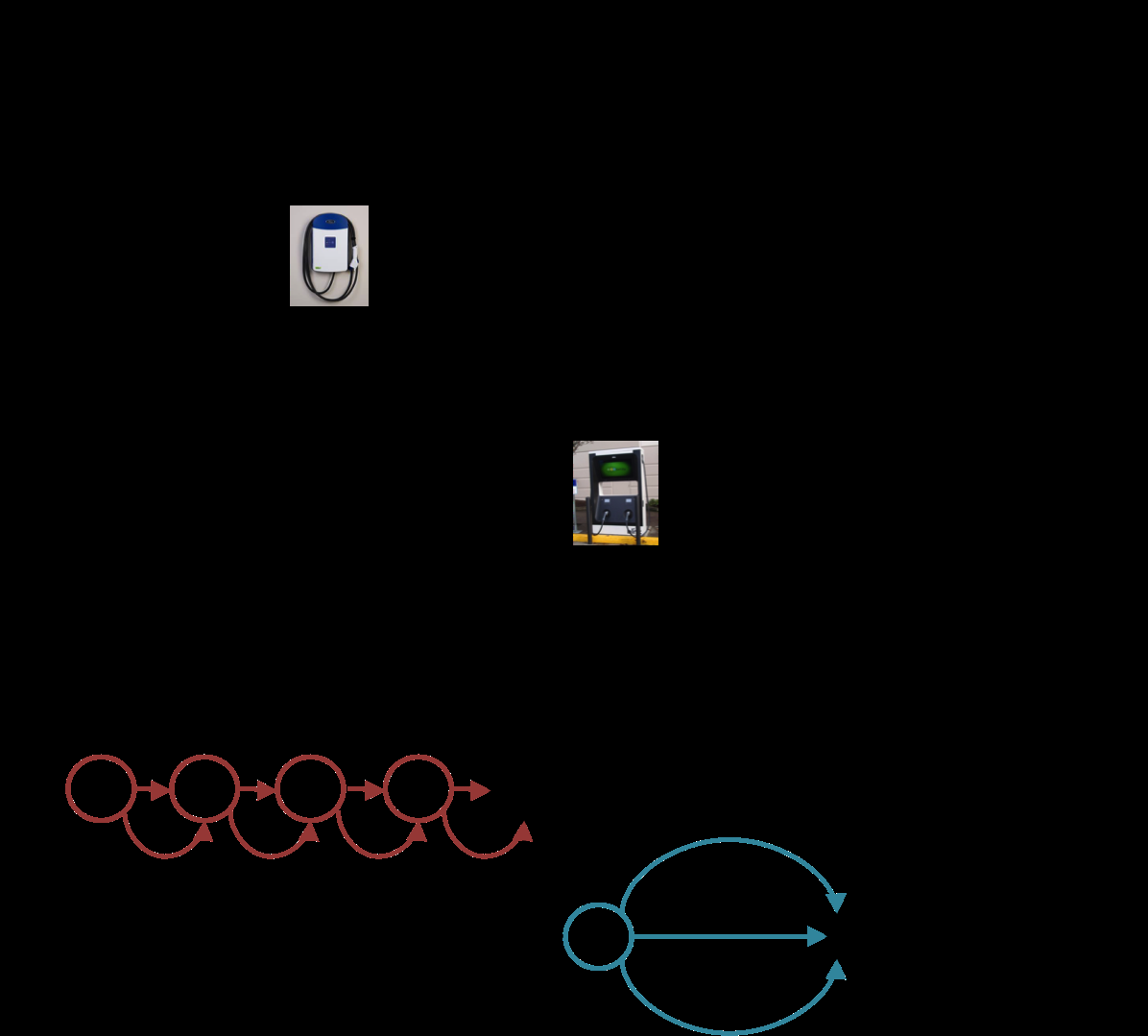
为了捕捉旅途中途停留充电所带来的时间延迟，并考虑充电决策相关的电费，我们将用户的充电决策建模为整体出行规划问题的一部分。具体方法是将充电决策建模为在虚拟扩展交通网络中的虚拟弧段上行驶的选择（见图1）。

定义 II.1 （虚拟交通网络）

我们通过将每个节点 v ∈ V替换为充电站的子图 Gv，该子图包含虚拟节点 Vv 和弧段 Av，从而定义一个新的图 Ge=(V e, Ae )：
- （I型充电站） 当充电可中断时， Gv是由 T个节点组成的一条链（在图1中以红色表示）。链中的每个节点通过两条平行弧段与下一个节点相连，这两条弧段表示在一个单个离散时间周期内的充电/不充电决策。
- （II型电站） 当充电不可中断时， Gv是一组平行弧段，表示选择的快速充电选项，包括在此充电站不充电的决策（在图1中以蓝色表示）。

请注意，不充电决策等同于具有零行驶时间和零获取能量的弧段。最后，我们将由于I型（相应地，II型）充电站而增加的虚拟弧段集合记为Ae I （相应地，Ae II ）。

与虚拟弧 a 相关的充电负荷曲线表示为 `a(t)。该曲线的积分为获得的总能量，用 εa 表示虚拟弧 a 的总能量。此外，我们还用 εa 表示电动汽车在由弧段 a 表示的道路路段上行驶所获得的能量。显然，对于表示道路路段的弧段， εa 通常为负数；而对于表示充电的虚拟弧段， εa 为正数。我们将需要在该交通网络上行驶的电动汽车驾驶员根据其起点、目的地、电池容量以及首次到达起点时的电池荷电状态（SoC）划分为若干类别。同一类别 c中的所有电动汽车具有相同的约束条件，因此可以选择类似的行驶路径和充电选项。以某种方式充电或选择特定驾驶路径的决策，可以表示为在虚拟交通网络上选择一条路径 k:=(a1,…,a|k|)，使得对于所有 i满足ai ∈ A e。在符号使用上略有简化，我们用 |k|表示路径 k的长度。

将第 c类电动汽车从其起点 oc运送到目的地 dc的所有可行路径的集合记为 Kc。注意，对于所有 k ∈ Kc， a1的头节点是起点 oc，而 a|k|的尾节点是目的地 dc。一条路径转化为电动汽车的行驶与充电计划，且在行驶过程中电池电量从不耗尽时，该路径对电动汽车是可行的。

定义 II.2.（虚拟网络上的可行路径）

一条路径 k在 Ge 上是能量可行的，当且仅当
ε min ≤ Initial SoC+ ∑ a ∈ links visited up to node v ε a ≤ ε max , ∀ v ∈ k,

其中 εmin表示为避免续航焦虑所需的最小充电量， εmax 表示电池容量。

由于 εa是给定的常数，我们可以枚举每个类别中的所有此类路径并形成 Kc，而无需考虑交通状况。或者，我们还可以基于不同的能量平面进一步扩展虚拟网络，以反映不同的电池电量水平。这超出了本文的范围。

与通信和数据网络不同，交通网络上的出行并非几乎瞬时完成。此外，由于出行需求的动态变化特性，交通网络中不同链路的通行时间以及电动汽车插电事件的发生频率均表现出时间变化。

定义II.3（随时间变化的流）

我们将每个弧 a ∈ A 在时间间隔 T=[0, T）内的车辆流流量速率表示为函数 λa （t）： T → R+。由沿路径 k 行驶的车辆所引起的流 λa （t）的部分记为 λa，k（t）。我们假设所有在时间 t 从弧 a 的尾部进入的车辆，恰好在 τa，t ∈ N 个时间单位后到达其头部。此外，我们假设时间间隔 T 的选取使得对所有满足 t 且 t+ τa，t ≥ T, ∀a 的时刻， λa（t）= 0 成立。

相应地，我们可以写出每条路径 k 上车辆的流量守恒。如果在时间 t 开始行驶时，路段 a 的行驶时间为 τa,t 个时间单位，且路径 k 上的下一个路段索引为 a′， 则根据流量守恒：
λa,k(t)= λa′,k(t+ τa,t). (II.1)

该线性方程组完整描述了车辆在充电和交通基础设施上的流动情况。然而，由于行驶时间τa,t具有时变特性，因此无法直接将其映射为虚拟网络 Ge上的传统网络流问题。

为了更好地将车辆在充电和交通基础设施上的移动视为网络流量问题，我们假设每条弧上的通行时间τa,t为积分值，并且我们研究电价问题的时间范围Ge为积分时间范围 T。

定义II.4 （时间扩展虚拟交通网络）

通过创建 Ge 的 T 个副本构成时间扩展网络 Gx = （Vx, Ax），这些副本标记为 Ge 0 到 Ge T−1 ，其中节点 v 的第 t 个副本表示为 vt。流经 Ge t 的流量对应于在时间 t 进入每条弧段的流量。对于每一条从节点 v 指向节点 w 的弧段 a ∈ A e，我们在 Ax 中引入一组弧段 {（v t, w t+τ a,t ）|t+ τ a,t ≤ T}。

已知，在区间 T ∈{0, 1,…, T − 1}上的动态网络流优化等价于此时间扩展网络[15]中的静态流优化。在求解静态流优化问题后，我们可以将弧 a t 上的静态流解解释为仅在时间区间 t进入弧 a的流量速率。因此，在本文后续部分，我们可以依据此定义来研究定价策略对总充电需求动态的影响。

在下一节中，我们将每位驾驶员为选择其最低成本充电选项而求解的优化问题，表述为该时间扩展网络上的最短路径问题。

III. 个体驾驶员优化与均衡拥堵

我们假设每位驾驶员都与特定的充电网络运营商（ CNO） r ∈ R签订了订阅服务。我们并未对CNO之间用户每日的客户切换行为进行建模。然而，我们假设从长远来看，存在失去客户给竞争对手的风险（或市场法规的约束），这激励充电商运营方将边际价格传递给其终端用户。

时序扩展网络上的最短路径问题

由充电网络运营商 r服务的电动汽车群体可属于一组类别 c ∈ Cr。每位个体用户会选择成本最低的充电选项和道路路段组合，以从出行起点前往目的地。通过弧段 a所需的通行时间由延迟函数τa,t表示。我们假设电动汽车的引入不会影响交通系统的均衡通行时间。因此，我们可以将通行时间τa,t视为可从历史数据（例如谷歌地图）中获取的确定性外生变量。相反，我们的重点是设计一种定价策略，以优化网络中分散布置的充电站的使用，同时考虑其有限容量以及电力时空可变价格。接下来将描述影响驾驶员选择路径 k ∈ Kc决策的成本因素。

用户在行驶弧段a时产生的不便成本与在弧段上花费的时间成正比：
sa(t)= γ · τa,t, (III.1)
其中 γ表示每位用户单位时间的同质价值。

除了时间成本外，驾驶员还会考虑充电电费。每个充电站 v ∈VI ∪ VII在时刻 t都有相应的电价 pv(t)。这种随时间和地点变化的电力价格反映了电网中的供电能力和拥堵情况，将在第四节中详细讨论。因此，如果电动汽车驾驶员选择通过选择虚拟弧 a ∈ Av（参见定义 II.1）在位置 v充电，则他/她将支付：
ρ a(ta) =∑ t a +τ a τ=t a pv(τ)`a(τ − t a) , (III.2)
其中 t a是车辆进入虚拟弧 a的时间，即开始充电的时间。

因此，在充电站没有增加等待时间的情况下，个体从时间 t开始沿路径 k所产生的成本等于：
ω k(t)= |k| ∑ i=1 (1ai / ∈ Ae I · sai (tai )+1 a i ∈ Ae I ∪ Ae II · ρai (tai )), (III.3)

其中，上述公式中的1ai∈/Ae I是指示函数，当ai∈/ Ae I成立时其值为1，否则为0。车辆进入弧段 ai的时间由下式给出
tai+1= tai+ τai,tai. (III.4)

关于在不同设置下高效求解电动汽车最短路径问题的数值方法，参见[9],[14],[16]及其内部参考文献。该问题并非本文的重点。相反，我们希望设计系统层面的聚合定价策略，以引导电动汽车群体实现更具社会和环境可持续性的足迹。因此，接下来我们将讨论由这些个体最短路径决策所引发的均衡。

B. 广义沃德罗普均衡（队列均衡）

交通研究中最常用的规则是沃德罗普原则[17],，其描述了在给定网络状态（例如，就本例而言的行驶时间或充电价格）的情况下，个体如何选择路径完成出行，以及这些决策如何导致网络中的均衡拥堵模式。尽管此处我们假设个体决策不会影响交通网络中的拥堵情况，但驾驶员仍会在充电站争夺有限的充电容量。因此，为了描述虚拟交通网络上充电站的均衡使用模式（定义 II.4），我们简要陈述沃德罗普原则，并引导读者参考 [17]以获取详细讨论。

沃德罗普第一原则指出，对于每一对起讫点对，驾驶员实际使用的各条路径的出行成本相等，且低于任何单个驾驶员在未使用路径上所经历的成本。因此，没有任何驾驶员能通过单方面改变路线而获益。沃德罗普第二原则指出，平均出行成本最小化。这意味着所有被使用的路径对驾驶员而言都具有相同的最小边际成本。

本文考虑的拥堵源在于充电站某一时刻只能容纳有限数量的电动汽车。这意味着我们需要对分配给每个充电站的虚拟弧段上的电动汽车数量施加容量限制。显式有容量限制的用户均衡问题的解将满足沃德罗普第二原则的一种修正形式，其中传统的出行成本被广义化，以反映当链路流量达到其容量时，在有容量限制的链路上可能形成的等待队列所带来的不便[18]。数学上，如果我们用 f c c ∈ Cr类 电动汽车数量，则此队列均衡可由以下方式刻画：
f c k(t)> 0=⇒ ω c k(t)+ ξ c k(t)= π c (t), ∀k ∈ Kc
f c k(t)= 0=⇒ ω c k(t)+ ξ c k(t) ≥ π c (t), ∀k ∈ Kc , (III.5)

其中 ω c k (t)由(III.3)给出， ξ c k (t)表示选择在时刻 k行驶路线 c的驾驶员类别所承受的不便成本 t由于在充电站形成的队列中等待而产生的体验。

我们将在第五节‐C部分讨论一种特定的零售电价机制，该机制可将社会最优聚合出行行为作为沃德罗普均衡实施，且可能在充电站无需等待。但首先，我们将在下一节简要讨论批发电价的传统机制。这是表征充电网络运营商（CNO）所产生成本所必需的。

第四节 独立电力系统运营商的经济调度问题

为了满足电网上的整体电力需求，一组发电机位于电力网络的不同母线上。本文给出了当前大多数独立电力系统运营商（IPSO）用于以社会最优方式调度这些发电机并出清批发电力市场的最简单模型。我们用 GP= (B, L)表示定义电网的图。在时间t的总发电量记为g t=[gb(t)]b∈B，网络化基础设施的外生负荷记为 t=[ b (t)]b∈B。交通网络 G与电力网络相耦合。每个充电站对应一条母线，即我们有VC:= VI ∪ VII ⊆ B。类似地，对应于充电站所需的负荷记为dt=[db(t)]b∈B，使得 db (t)= 0当 b∈/ VC时成立。我们将在下一节讨论 db(t)与 车辆流之间的关系。

定义可行调度有两个约束条件。首先，电网的供需平衡要求必须得到满足，即：
1T(dt+`t − gt)= 0, ∀ t ∈ T. (IV.1)

其次，在直流近似下的输电线路潮流约束[19]应当成立：
H(dt+`t − gt) ≤ m, ∀ t ∈ T, (IV.2)

其中矩阵H在[19],中明确定义，m=[mf]f∈L 是包含输电线 路潮流限值的向量。

独立电力系统运营商通过求解经济调度问题来决定gt，以最小化整体系统成本[20]：
min gt≥ 0,t ∈T ∑ t ∈T 1 T c(gt) (IV.3) s.t. 约束(IV.1)和(IV.2),

其中， c(gt) :=[cb(gb(t))]b∈ B 是一个表示严格凸且连续的发电成本的向量。此外，如果分别为约束条件 (IV.1) 和 (IV.2) 引入拉格朗日乘子 γ t 和 µt ，则不同节点处的电能价值 b ∈ B，即节点边际电价(LMP)pt =[pb( t)]b∈ B 为：
pt = γ t 1+ H T µ t . (IV.4)

如果需求也是灵活的，独立电力系统运营商应通过在可行的选择集合内选取最优的需求值来最小化成本。如果转移或削减需求是可能的但会产生成本，则该成本可以添加到 (IV.3) 的目标函数中。

V. 定价机制 MECHANISMS CONSIDERING 电动汽车 MOBILITY

A. 聚合网络流模型

为了建模充电站需求的动态变化，我们假设每个服务提供商都能获取其所服务的所有电动汽车驾驶员的出行计划。这一假设在智能交通系统中非常常见。像特斯拉这样的公司已经为电动汽车车主提供内置导航和充电引导服务，同时运营快速充电站。

对于每个零售商 r，路径 k 上时段 t 的弧 a 中的车辆流表示为弧流量λr a,k(t)。如第二节所述，网络上的链路流量必须守恒，即 λr a,k(t) = λr a′,k(t+ τa,t)。此外，为了模型化个体电动汽车驾驶员路径选择对网络流量的影响，每条路径上第一条弧的弧流量 k 必须满足：
λr a1,k(t)= fr k(t), ∀ k ∈ Kc, c ∈ Cr, ∀r ∈ R, (V.1)
其中，path flow fr k(t) 表示在时间 t 从路径 k 出发、隶属于零售商 r 的车辆流。如果用 ur c(t) 表示在时间 t 到达的类别为 c 的车辆总数，则必须满足：
∑k∈Kc f r c(t), ∀ t ∈ T. (V.2)

将弧段流量向量表示为λr=[λr t]0≤t≤T，其中向量λr t 包含所有λr a,k(t) ∀k ∈ Kc, c ∈C r 的值。同时，我们将路径流量向量表示为fr=[fr k(t)]0≤t≤T,k∈Kc,c∈C r。如第二节所述，上述关于弧段流量和路径流量的约束条件可以写成一个线性方程组。为简洁起见，我们可以将这些约束条件表示为：
vec(λ r )= Srvec(fr), ∀ r ∈ R, (V.3)
对于某个具有适当维度的矩阵 Sr。

在时刻 t，由于零售商 r 拥有的位于母线 b 的充电站所产生的电力需求是相关弧段流量的函数。设 Ae b 为与充电站 b 相关的在 Ge 上的虚拟弧段集合。因此，该充电站的总需求为：
d r b( t)= ∑ a ∈A e b ∑ c ∈C r ∑ k ∈Kc `a(t)? λ r a,k(t), (V.4)
其中算子 ? 表示卷积操作。

我们假设存在一种可行的流量模式，使得所有用户都能完成行程，而无需在充电站排队。如果一个时间流满足充电站的容量约束以及每辆电动汽车的能量可行性约束，则该时间流是可行的。因此，在每个时刻 t，在零售商 r 拥有的充电站 b 上插电的车辆数量必须始终低于站点容量 n r b 。记车辆选择虚拟弧 a 时插电的持续时间为θ a。为了满足容量约束，我们需要满足：
∑ a ∈ Ae b ∑ c ∈ Cr ∑ k ∈ K c Π( t θ a) ? λ r a,k(t) ≤ n r b , ∀ t ∈ T, (V.5)
其中 Π(·) 表示[0,1]之间的单位脉冲。

B. 考虑移动性的经济调度与批发市场节点边际电价

根据上述模型，我们可以方便地描述考虑车辆移动性和充电站容量的独立电力系统运营商的经济调度问题如下：
min fr≥0,gt≥0,t∈T ∑ t∈T[1T c(gt)+∑ r∈R γrτ t Tλr t] (V.6)
s.t. Constraints(IV.1)&(IV.2), (V.7)
Constraints(V.2)&(V.3), (V.8)
dt=∑ r∈R Mr tλ r, Qtλ r ≤ nr, ∀ t ∈ T, (V.9)
为简洁起见，我们已将 (V.4) 和 (V.5) 中的卷积方程通过矩阵Mr t和Qt映射为 (V.9) 中的矩阵‐向量形式。

命题V.1. （分布式市场出清） 如果充电商运营方与独立电力系统运营商合作，则经济调度问题(V.6)可以以分布式方式求解。这将消除对复杂投标的需求。

证明概要： 我们可以证明，优化问题 (V.6) 可被分解为多个具有可分目标函数的子问题，这些子问题通过约束条件 (IV.1) 和 (IV.2) 耦合。第一个子问题是独立电力系统运营商在 (IV.3) 中求解的经济调度优化问题，其节点边际电价pt按 (IV.4) 计算。其余子问题分别对应各个充电商运营方 r ∈ R 求解各自的路径与充电优化问题，以最小化自身成本，如下所示：
min λr t ,∀t∈T∑ t∈T p T t M r tλ r+ γrτ t Tλr t (V.10)
s.t. Constraints(V.2)&(V.3), Qtλ r ≤ nr, ∀ t ∈ T.
将 (V.6) 分解为由独立电力系统运营商和充电商运营方求解的更小子问题，使我们能够使用对偶分解方法以分布式方式计算最优的节点边际电价pt[21],[22]。因此，通过迭代发布一个先验的节点边际电价pt（以足够小的步长进行更新），并要求充电商运营方通过私有求解 (V.10) 来估计其电动汽车用户群体对该价格的响应，独立电力系统运营商仍可实施在 (V.6) 中计算出的最优结果。

C. 具有有限站点容量的动态零售定价

个人不会遵循充电网络运营商（CNO）关于充电地点的指令。相反，在一个采用动态零售定价的完全竞争充电站市场中，充电商运营方将实时节点边际电价（LMP）传递给个人，由个人自行做出选择。在这种情况下，根据 (III.5)，每位驾驶员会选择使 ω k( t)+ ξ k( t)最小化的路径，即行驶时间加上充电电费以及在充电站队列中的排队等待成本之和最小。这将导致由(III.5)所描述的队列均衡。

引理V.2。 与约束 Qt λ r ≤ n r 在(V.9)相关的拉格朗日乘子向量的值，等于在队列均衡情况下，在每个充电站形成的队列中等待的成本。

该引理针对带侧约束的交通网络的一般情况在[18]中得到证明，其结果通过我们对虚拟弧段的定义可直接推广到电动汽车充电站的情况。队列（尤其是较长的队列）可能不切实际且令人烦恼。在充电站由于作为有限容量资源具有共享性质的情况下，若充电网络运营商不希望在充电站形成任何排队，则充电的最优动态零售电价不再等同于节点边际电价pt。

定理V.3（无队列充电站的高效零售定价） 在完全竞争充电站市场中，充电网络运营商 r 在其充电站收取的边际动态零售电价由两个随时间和空间变化的部分组成：一个边际容量附加费 νr t=[νr b（t）]b∈B ，加上电力的节点边际价格pt。该容量附加费νr t等于与（V.10）中的约束Qtλ r ≤nr相关的拉格朗日乘数，并应在电动汽车占用充电站车位的所有时段 t内支付。因此，选择在时间 τ、地点 b开始的对应于虚拟弧 a的充电选项的总零售成本等价于：
Retail cost= ∑_{t=τ}^{τ+τa} [νr b(t)+`a(t − τ)pb(t)]. (V.11)

证明概要： 该定理直接通过证明(V.10)的一阶必要最优性条件等价于施加了容量附加费 νr b(t)的广义沃德罗普均衡(III.5)的条件而得出。拥堵附加费通过向电动汽车驾驶员收取与他们在充电站因在队列中等待空位而浪费的时间所产生的成本相同的费用，确保充电站不会形成队列（参见引理V.2），从而使得驾驶员的状况与其不存在时完全相同。

VI. 数值结果

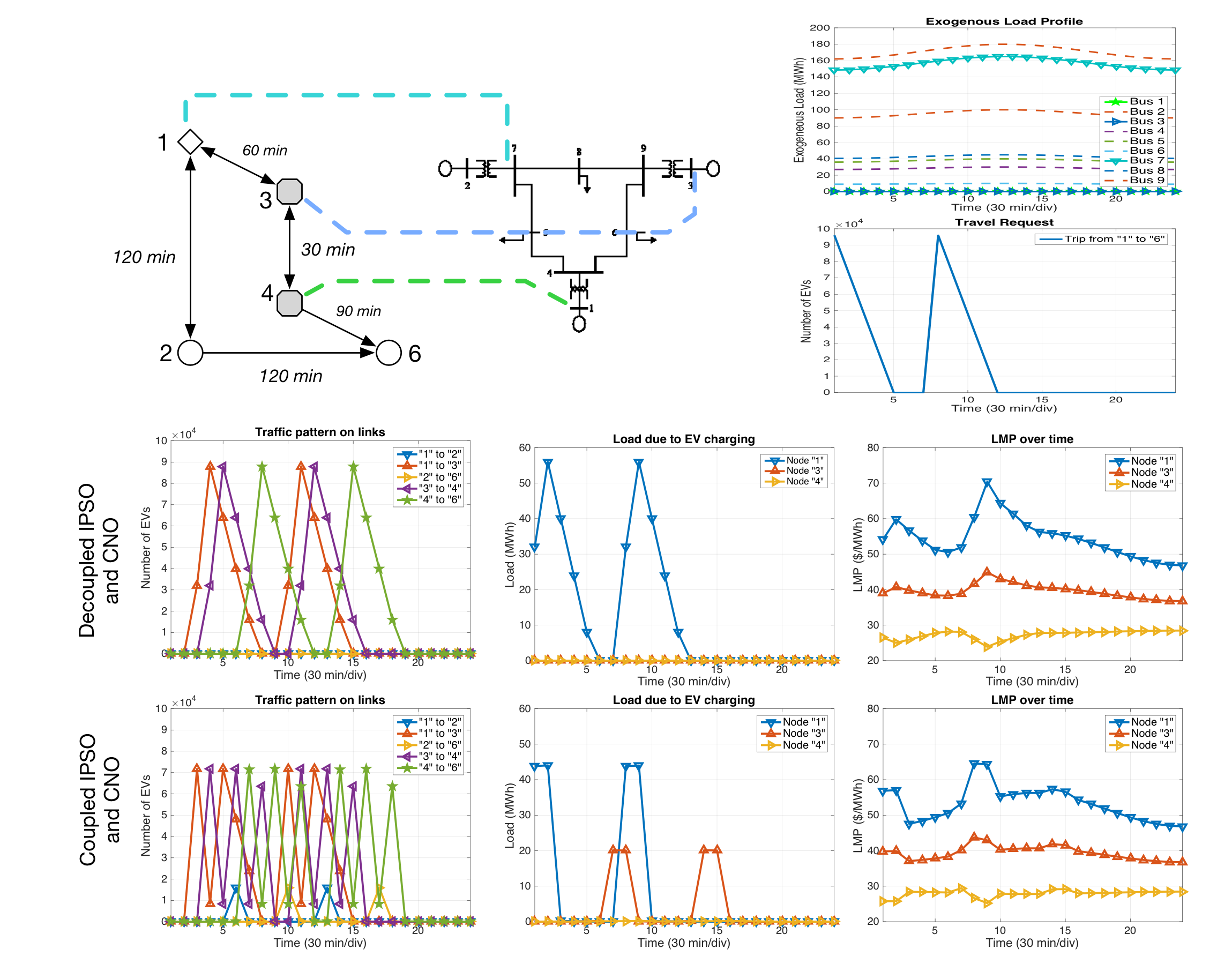
我们考察在交通网络 G（如图2所示）下(V.6)的解，而电力网络 GP是叠加在交通网络上的改进型IEEE 9节点系统。我们考虑在12小时时间跨度内以30分钟时间步长进行交通模式优化和经济调度，即 T= 24。为了使结果易于解释，假设每辆电动汽车行驶30分钟消耗1千瓦时电能，且 γ r = 0.1。I型和II型充电站每30分钟可充电2千瓦时，电动汽车最多可在出行前1小时选择使用I型充电站。假设 a(t) 为平方函数，使得 a(t) = 1/2 对于 t= 1,2成立。充电站的容量限制设为 6×10⁴。外生负荷曲线和出行请求曲线也显示在上图中。注意到有驾驶员希望在t= 1, 2,3, 4（批次1）以及 t= 8, 9, 10, 11（批次 2）开始出行。从负荷曲线可以看出，位于‘3’、‘4’（途中的充电站）的充电价格应低于‘1’（即起点）处的充电价格，由于一种较小的外生负荷，尤其是在接近 t= 12且负荷处于峰值时。

我们首先考虑用户在出行规划中不考虑电力成本时的交通/充电模式。如中间一行的中间图所示，所有电动汽车均选择在起点充电，因为这是时间效率最高的选项。然而，由于起点节点连接到一个外生负荷较大的母线（母线‘7’），该节点的电力成本也较高，这可以从右侧的节点边际电价图中看出。

另一方面，当充电网络运营商（CNO）和独立电力系统运营商（IPSO）的优化耦合且零售电价反映电网拥塞情况时，我们发现部分电动汽车被引导至途中充电，即在节点 ‘3’充电（参见下中图），因为该处提供的电价（LMP）较低。有趣的是，我们还观察到一些电动汽车选择了从‘1’ 到‘2’的路径，尽管该路径并非时间效率最高，这是由于考虑了充电站拥堵的影响所致。最后，我们还发现，联合优化所产生的节点边际电价（LMPs）相较于分离式解决方案具有更平滑的分布特征。

VII. 结论与未来工作

我们提出了一种动态零售定价机制，该机制在考虑充电站的有限容量、电动汽车移动性以及电力价格的时空变化特性的情况下，可引导实现电动汽车充电站的社会最优使用。仍有许多问题需要在未来的研究中进一步探讨。高维度可能导致所提出的算法出现计算难题。由于时间扩展，生成的网络规模随 |T |线性增长。另一个需要深入研究的问题是充电网络运营商之间的竞争及其零售定价机制。本文假设消费者订阅单个充电网络运营商，这使得我们可以假设每个充电网络运营商能够学习出行模式，并将其作为问题的输入，从而消除了充电网络运营商之间竞争的日间影响。