基于博弈论的边缘计算激励机制

基于伯特兰德博弈的机会式边缘计算激励机制

摘要

在真实的边缘网络中，许多节点可能是自私的，不愿意为其他节点转发消息。在这种情况下，需要一种激励机制来鼓励自私节点参与消息转发。本文分析了边缘机会网络中源节点与中继节点之间的交互，提出了一种基于博弈论的激励机制以促进节点间协作。首先，我们定义了源节点与中继节点之间的交互步骤，包括源节点决定消息转发的价格、中继节点向源节点响应转发方案，以及所有参与消息转发的节点均可获得奖励。我们为节点提供两阶段激励，即节点在接收和转发消息时均可获得奖励。由于节点可能具有自私性，源节点和中继节点都希望最大化自身的效用。随后，我们将源节点与中继节点之间的协作建模为伯特兰德博弈，并定义了源节点和中继节点的效用函数。进一步地，我们证明了纳什均衡的存在性和唯一性，并给出了源节点的最佳定价方案和中继节点的最佳转发方案。仿真结果表明，所提出的激励机制能够促进自私节点间的协作，并在投递率和延迟方面提升路由算法的性能。

索引词 边缘计算，机会网络，激励机制，博弈论。

一、引言

随着移动终端和无线技术的发展，机会式边缘网络[1]正日益成为热门研究课题。机会式边缘网络由无线自组织网络和延迟容忍网络（DTN）[2]演化而来。在传统无线自组网中，数据传输要求源节点与目的地节点之间至少存在一条完整的通信链路。然而，在实际环境中可能存在长时间的网络中断，无法保证源节点与目的地之间的正常通信。与传统网络不同的是，在机会式边缘网络中，源节点与目的地之间不需要完整的链路，节点间的消息转发通常是机会式的，并基于节点移动[3]进行。机会网络使用存储携带转发路由进行数据传输。也就是说，如果节点未找到合适的中继节点，消息将被存储在其缓冲区中，并在移动过程中携带这些消息，直到找到合适的中继节点，然后将消息转发给中继节点，并通过若干中间节点逐步转发，最终消息到达目的地。

从机会式边缘网络的路由方案中可以发现，源节点与目的地之间的通信可能涉及多个节点参与，而数据传输的成功依赖于节点间的协作[4]。因此，数据传输的前提是路由路径中的中间节点愿意转发数据包。但在许多应用中，作为机会网络中节点的移动设备属于不同且独立的所有者。由于节点的能力、内存空间、电池电量及其他资源受限，节点可能倾向于自私行为。它们可能只愿意接收消息，而拒绝接收那些对自己无用但对他人有益的消息。如果所有节点都是理性的，节点将表现出自私性，试图节省自身资源而不为其他节点转发消息。在[5]中，作者指出节点的自私行为严重损害了机会网络中数据传输的性能，而对节点进行激励可以改善网络的整体性能。

目前，机会网络中的激励机制分为三类：基于TFT（以牙还牙）的机制[6]、基于信誉的机制[7]–[9]以及基于信用的机制[9]–[10]。TFT（以牙还牙）机制的核心思想是利用博弈论根据互惠原则构建模型，节点向其他节点转发与其从对方接收到的数据量相同的数据。在实际网络环境中，由于存在不对称业务，基于TFT的机制难以获得良好的性能。在基于声誉的激励机制中，每个节点的历史协作行为被记录下来，并为其分配一个声誉值以判断其是否自私。此外，声誉值是动态变化的，参与消息转发的节点将获得声誉值的提升，声誉值较高的节点更有可能被选中来转发消息。然而，声誉机制无法有效区分高信誉节点与信誉值等于或略高于合法阈值的节点，导致对节点的激励效果较差。在基于信用的激励机制中，源节点需向转发消息的中间节点支付虚拟货币，需要第三方管理，且未针对不同节点制定差异化的定价方案。

如上所述，每种激励机制在刺激节点为其他节点转发消息方面都存在其固有的缺点。本文将博弈论和虚拟货币应用于节点间交互的分析中，提出一种将节点协作建模为伯特兰德博弈的激励机制。通过所定义的定价方案和激励机制，达到纳什均衡，使每个节点获得最大效用。与现有研究不同，所提出的机制对消息传输采用两阶段激励。由于节点中的消息传输包含两个阶段，即从源节点接收消息以及将消息转发给其他节点，因此应激励每个节点不仅从源节点接收消息，而且向其他节点转发消息。本文的工作促进了节点参与消息转发的积极性，并提升了数据传输性能。

本文的其余部分组织如下。在第2节中，我们描述并分析了相关激励机制。第3节详细介绍了基于伯特兰德博弈的激励机制。在第4节中，我们描述了基于博弈论的定价分析。仿真实验被展示并在第5节中进行了讨论。最后，我们在第6节中总结了本文。

二、相关工作

机会路由已被广泛研究，针对“存储携带转发”式的数据传输，提出了多种类型的消息转发方法和路由算法，旨在提高数据投递率，同时降低网络开销。Epidemic路由[11]将消息洪泛到所有节点，而不考虑路由开销。理论上，Epidemic路由具有最高的数据投递成功率。直接传输[12]要求源节点存储待发送的数据，且仅在遇到目的地时才转发数据，不向任何其他节点转发。直接传输在所有路由算法中开销最低，但其数据投递成功率也最低。预言路由[13]基于投递可能性选择下一跳。如果中继节点的投递可能性高于某一阈值，则将消息转发至该中继节点。预言路由根据历史信息动态更新链路的投递可能性值。节点相遇越频繁，投递可能性越高；若两个节点长时间未相遇，它们之间的投递可能性可能会降低。在某些场景下，预言路由可实现较高的投递率和较低的开销。还有其他路由算法[14]–[16]，在投递成功率与网络开销之间进行权衡，在某些特定场景中表现出良好的性能。然而，这些传统路由算法的前提假设是机会网络中的所有中间节点都愿意为其他节点转发消息。在实际环境中，作为机会网络节点的移动设备属于不同且独立的所有者。由于节点的能力、内存空间、电池电量及其他资源的限制，节点可能倾向于表现出自私行为。在Epidemic路由中，如果所有节点都具有自私性，则该路由方案将退化为直接传输。

近年来，机会网络中节点的自私性问题已引起众多研究人员的关注。在[17]中，作者探讨了节点协作对一些代表性路由算法（如Epidemic、两跳[18]、二元喷洒与等待[19]等）的影响。作者提出了一种简单的激励机制，通过定义合作度来提升这三种路由算法的有效性，并发现节点之间的合作度会影响网络的投递率。在[5]中，作者研究了节点自私行为如何影响网络性能，结果表明，节点自私性会导致投递率下降以及消息传输延迟增加。人们普遍认为，在机会网络中需要为节点提供激励以克服搭便车问题，即某些节点请求他人转发自己的数据包，但自己却不参与转发。

避免帮助他人。目前研究的激励机制主要有三种类型：声誉、物物交换（或以牙还牙）和虚拟货币。在[20]中，作者提出了一种使用公平定价机制的拍卖激励机制来激励节点，并将定价过程建模为一个拍卖博弈。该博弈可达到贝叶斯纳什均衡，在此均衡下每个中间节点的利润均可最大化。在[21],[22]中，作者提出了一种称为MuRIS的激励机制，使节点能够通过选定路径利用少量传输协同传递彼此感兴趣的信息。在[23]中，作者提出了一种基于博弈论的多功能激励方案——Multicent，不仅提供合作激励，还鼓励节点遵循既定规则以实现期望的性能目标。在[24]中，作者从博弈论的角度为自私的机会网络提出了一种感知激励的路由方法，综合考虑个体自私性和社会自私性，以提升机会网络的性能。该方案将两个节点之间的消息传输映射为鲁宾斯坦‐斯塔尔讨价还价博弈，采用虚拟货币并构建适当的价格函数，同时考虑节点的资源和社会关系进行数据传输。该方案的缺点是数据传输中的能耗和延迟消耗较高。在[25]中，作者提出了一种基于双重拍卖的拥塞感知的节点协作机制，其中节点根据当前空闲缓冲区和消息接收速度确定自身的拥塞程度。然后结合消息投递概率与拥塞程度，节点基于双重拍卖模型进行消息交易。在[26]中，作者提出了一种名为SEIR的路由协议，该协议基于斯塔克尔伯格博弈论模型，并给予中间节点最优奖励，以消除节点的自私性。在[27]中，作者提出了一种基于博弈的激励策略（GIS），该策略利用基于双人交易的三阶段讨价还价模型，允许发送节点根据博弈得出的最优价格直接向中间节点支付，而无需任何第三方。

上述激励机制促使节点参与消息投递。然而，节点参与消息传输包含两个阶段：第一阶段是从源节点接收消息，第二阶段是伺机将消息转发给其他节点。如果某些节点仅接收消息，拒绝长期存储消息，并最终不将消息转发给其他节点，则可能导致消息丢失。由于上述机制仅为消息投递提供一次性激励，无法最大程度地激励节点积极参与消息传输，而两阶段激励机制能更好地激发自私节点的参与度，提高消息投递成功率。在现有研究基础上，我们设计了一种结合博弈论[28]和信用的激励机制以提升路由性能。在本机制中，消息传输采用了两阶段激励机制，每个节点都能够鼓励节点从源节点接收消息并将其转发给其他节点。

III. 系统描述

我们提出了一种基于伯特兰德[30]博弈的激励机制（BGI），以激励自私节点参与机会网络中的消息传输。BGI包括节点间交互的定义、参与消息传输节点的奖励机制以及定价机制。在本节中，我们介绍了机会网络中节点间交互模型的详细内容。我们将消息传输过程视为一种商品交易。假设携带消息的节点是市场中的买方，而源节点向中间节点购买消息传递服务。中间节点则是向源节点出售消息传输服务的卖家，并从源节点获得奖励。显然，消息传输可被视为市场中的商品。

A. 交互模式

在机会网络中，假设节点数量为n，节点集合为N={1, 2, · · ·i · · · n}。一个节点可能携带多个消息，因此它可能不仅是某条消息的源节点，也可能是另一条消息的目的地，并且还可以在消息传输过程中充当中继节点。但是，一个节点一次只能为另一个节点转发一条消息。在我们如图1所示的模型中，消息发送者称为源节点，准备接收并转发消息的节点称为中继节点。除了源节点和中继节点外，还存在许多交换点，这些交换点可以与基站、服务器或其他固定或移动基础设施集成。节点可通过参与消息转发从交换点获得虚拟货币。

在我们的模型中，源节点与中继节点之间的交互包含若干步骤。第一步，源节点广播消息转发请求，然后中继节点靠近源节点的是候选中继节点，它们接收请求并考虑是否为源节点转发消息。在第二步中，准备转发消息的节点向源节点反馈其转发每条消息的成本，不同节点的成本可能不同。在第三步中，源节点综合考虑所有中继节点的成本后，向不同的中继节点回复不同的转发消息价格，这些价格应能促使中继节点愿意接收并转发消息。在第四步中，各中继节点根据源节点给出的价格决定为源节点转发多少条消息，并将服务计划反馈给源节点。最后，源节点根据接收到的服务计划将消息发送给中继节点。

为了鼓励节点之间的协作，源节点和中继节点在参与消息传输时都将获得奖励。由于源节点无法在没有中继节点接收消息的情况下完成消息转发，因此中继节点在接收消息后可直接从源节点获得一定奖励。因此，源节点将消息转发给更多的中继节点时需要支付更高的成本。但源节点可以通过消息转发从交换点获得奖励，且转发次数越多，获得的奖励也越多。交换点是分布式的，可集成于其他固定或移动设备中并位于任意位置。当源节点遇到交换点时，将因其已完成的消息转发任务而从交换点获得虚拟货币。

在消息的单跳传输中，存在两个阶段：源节点转发消息和中继节点接收消息。为了最大程度地激励参与者，我们为每个参与消息传输的节点设计了两阶段激励机制，即节点可以通过接收和转发消息获得奖励。对于源节点而言，其转发消息的奖励来自交换点提供的c虚拟货币。而对于中继节点，其接收消息的奖励则直接由源节点提供。此外，消息转发可通过交换点根据发送方和接收方的报告进行验证。一旦中继节点接收到消息，它将在下一轮中成为源节点，并按照上述步骤寻找其他节点以转发消息。该过程不断重复，直到目的地节点接收到消息。

我们将源节点与中继节点之间的交互建模为商品交易过程，并利用博弈论寻找最优价格，以激励更多节点参与消息传输，从而实现最大效用。对于在博弈中充当买方的源节点而言，它们希望商品的价格尽可能低。然而，作为服务卖方的中继节点则期望更高的价格并出售更多的商品，因为这样可以获得更多的奖励。因此，在接收一条消息时，较高的价格将导致源节点获得的奖励减少，而中继节点获得的奖励增加。

在进一步讨论节点行为之前，我们提出一些假设。我们假设交换点是可靠的，能够根据节点的报告正确评估其是否转发和接收了消息。也就是说，交换点不会被节点欺骗。当节点连接并将其服务计划共享给交换点时，交换点能够准确计算其奖励，并且它们必定能从交换点获得相应的奖励。

B. 效用函数

从源节点与中继节点的交互可知，当中继节点接收到的来自源节点的价格大于其成本时，它将执行其服务计划，而该服务计划包括其希望接收的消息数量。对于源节点而言，它必须考虑所有中继节点的成本，并决定一个合理的价格，以在确保自身奖励的同时吸引尽可能多的中继节点。对于中继节点而言，其效用受到其决定接收的消息数量的影响。然而，一个节点接收的消息越多，其成本就越大。因此，中继节点的效用在一定程度上会达到饱和。

假设中继节点j接收到来自源节点ai的消息数量i，并且该ai消息数量将由节点j在下一轮转发给其他节点。然后，我们将中继节点j的效用函数定义为公式(1)，将源节点i的效用函数定义为公式(2)。

$$
U_j = p_j a_i - c_j a_i - b a_i^2 \quad (1)
$$

在公式（1）中，Uj是中继节点j的效用，pj是中继节点j从源节点i接收一条消息的价格，cj表示中继节点转发一条消息的成本，b是饱和系数。

$$
P_j = c a_i - p_j a_i \quad (2)
$$

源节点的效用i是向中继节点转发消息所获得的奖励j，转发的消息数量越多，效用越高。因此，源节点的效用与转发的消息数量成正比。在公式（2）中，c是由交换点给出的系统参数，并满足 $ c > p_j $，表示任意节点转发消息的价格。

C. 转发消息的实际成本

在源节点与中继节点的交互中，中继节点必须向源节点响应转发消息的成本。从长期来看，中继节点将向源节点反馈转发消息的实际成本。如果中继节点j向源节点提供虚假成本，则其收益并非最优，这一点在理论上可以证明。我们假设中继节点向源节点报告的虚假成本为cj，而源节点响应的价格为p′j。根据公式（1），其效用为U′j如所示方程（3）。

$$
U’_j = p’_j a_i - c_j a_i - b a_i^2 \quad (3)
$$

假设节点j转发消息的真实成本为cj，对应的j节点的价格和效用分别为Pj和Uj。比较Uj和U′j，可得方程（4）。

$$
U’_j - U_j = \left(c + \frac{c’_j - c_j}{4b}\right) - b a_i^2 - \left[\left(c + \frac{c_j}{2} - c_j\right)\frac{c - c_j}{4b} - b a_i^2\right] \quad (4)
$$

根据算术计算，我们可以得到U′j − Uj，如公式(5)所示。

$$
U’_j - U_j = \frac{(c’_j - c_j)^2}{8b} \quad (5)
$$

由于U′j − Uj < 0，U′j小于Uj。因此，对中继节点来说，向源节点告知转发消息的真实成本是最佳策略。

IV. 基于博弈论的定价分析

在我们的模型中，节点可以通过转发消息从交换点获得奖励，这激励节点参与消息转发。为了最大化效用，源节点应制定最优的定价策略，相应的中继节点应提供最优的服务计划。在本节中，由于源节点与中继节点之间的协作类似于伯特兰德博弈中卖家与买方之间的交互，因此采用伯特兰德博弈论来分析源节点与中继节点之间的交互。

在伯特兰德博弈中，源节点是买方，因为它有待发送的消息，并且需要中继节点提供的转发服务。中继节点是向源节点提供转发服务的卖家。显然，消息转发就是商品。如果商品的需求已知，源节点可以根据中继节点的成本计算出最合理的价格，从而使自身获得最大利润。如果源节点提出的价格低于中继节点的成本，中继节点将不会为其转发消息。对于中继节点而言，当所有源节点给出的价格确定后，它们会决定为每个源节点转发的消息数量，以最大化自身的收益。接下来，我们将分析双方的策略，并展示该博弈的纳什均衡[28]。

根据源节点的策略，中继节点将制定一种服务计划策略以最大化其效用。中继节点j的效用函数为公式(1)，我们可以得到Uj的一阶导数，如公式(6)所示。

$$
\frac{\partial U_j}{\partial a_i} = p_j - c_j - 2b a_i \quad (6)
$$

Uj的二阶导数为公式(7)。

$$
\frac{\partial^2 U_j}{\partial a_i^2} = -2b \quad (7)
$$

由于 $ b > 0 $，Uj的二阶导数为负。因此，Uj是严格凸函数。令Uj的一阶导数等于零，可得到Uj的最大值点，此时ai如公式(8)所示。

$$
a_i = \frac{p_j - c_j}{2b} \quad (8)
$$

如上所示，当源节点的策略（价格）给定时，中继节点转发的适当消息数量为 $ \frac{p_j - c_j}{2b} $，这将最大化中继节点的效用。

结合公式（8）和公式（2），可得到源节点的效用，如公式(9)所示。

$$
P_j = c \cdot \frac{p_j - c_j}{2b} - p_j \cdot \frac{p_j - c_j}{2b} \quad (9)
$$

然后我们可以得到Pj的一阶导数，如公式（10）所示。

$$
\frac{\partial P_i}{\partial p_j} = \frac{c - 2p_j + c_j}{2b} \quad (10)
$$

然后，Pi的二阶导数如公式（11）所示。

$$
\frac{\partial^2 P_i}{\partial p_j^2} = -\frac{1}{b} \quad (11)
$$

由于 $ b > 0 $，Pi的二阶导数为负。因此，Pi是严格凸函数，且存在最大值点。令一阶导数等于零，可得到最优价格pj，如公式(12)所示，该价格将最大化源节点i的效用。

$$
p_j = \frac{c + c_j}{2} \quad (12)
$$

根据上述分析，源节点i与中继节点j之间的博弈将在点 $ \left( \frac{c + c_j}{2}, \frac{p_j - c_j}{2b} \right) $ 处达到纳什均衡，这意味着源节点i的最佳策略是将转发价格定为 $ \frac{c + c_j}{2} $，而中继节点j的最佳策略是接收来自源节点i的 $ \frac{p_j - c_j}{2b} $ 条消息。

V. 仿真

为了验证所提出激励机制的效率，在ONE[31]仿真器中进行了仿真实验。在我们的仿真中，使用真实数据集 Infocom5 和 Infocom6 进行节点活动驱动，这些数据集可以从 CRAWDAD 下载。由于在上述数据集中得到的结果类似，本文仅展示了 Infocom5 和 Infocom6 的结果，详细信息如表1所示。在仿真中，每个节点以 0.5–1.5m/s 的速度移动。每 3000–4000 秒生成一条大小为 500KB 的消息。采用基于最短路径图的移动模型，地形尺寸为 4500 × 3400 平方米。系统参数 $ c $ 为 10，

参数	Infocom5	Infocom6
节点数量	41	45
消息大小	500 KB	500 KB
移动速度	0.5–1.5 m/s	0.5–1.5 m/s
缓冲区大小	20 MB	20 MB
仿真时间	36000 s	36000 s

且 $ b $ 在 Epidemic 路由算法和 Prophet 路由算法中分别为 1/2 和 3/2。我们发现，路由算法在上述参数取值下具有最佳性能，但我们也分析了参数 $ b $ 对路由性能的影响。

A. 性能指标

在实验分析中，使用交付率、平均延迟和开销比率作为性能指标，其定义如下。

投递率 ：投递率定义为成功到达目的地的消息总数（success_number）与消息总数（created_number）的比值。投递率越高，消息成功到达目的地节点的概率就越大。可以表示为:

$$
\text{投递率} = \frac{\text{success_number}}{\text{created_number}}
$$

开销比率 ：开销比率是转发失败的消息数量与成功传输到目的地的数据包数量的比值，其中转发失败的消息数量等于待转发的数据包总数（forward_number）减去成功传输到目的地节点的数据包数量（delivered_number）。开销越低，性能越好。其定义为:

$$
\text{开销比率} = \frac{\text{forward_number} - \text{delivered_number}}{\text{delivered_number}}
$$

平均延迟 ：平均延迟定义为消息从源节点生成到消息到达目的地节点所用时间的平均值，因此期望的平均延迟越低越好。

B. 仿真场景

众所周知，现有的路由算法基于节点间的协作。在本文中，我们运行 Epidemic 路由算法和 Prophet 算法，通过调整自私节点的数量来评估所提出的激励机制的性能。同时，我们假设所有自私节点均为逐利节点，当奖励高于成本时，它们一定会选择与其他节点协作。我们考虑以下六种场景。

(1) Epidemic+无自私节点（E+N） 。在 Epidemic 路由算法背景下，所有节点都愿意在没有任何激励的情况下为其他节点转发消息，并且能够相互协作。由于每个节点都承担参与消息传输时，此场景下的网络性能最佳。E+N 是性能比较的基准。

(2) Epidemic+自私节点 (E+S) 。在 Epidemic 路由算法背景下，我们在网络中引入自私节点，这些自私节点将拒绝在路由过程中转发消息。由于自私节点不与其他节点协作，网络性能必然会受到负面影响。

(3) Epidemic+自私节点+BGI(E+S+BGI) 。在 Epidemic 路由算法背景下，我们引入了自私节点，并采用所提出的 BGI 机制来激励自私节点与他人协作。在 BGI 的激励下，只要有利可图，自私节点就会为他人转发消息，理论上该场景下的网络性能将优于 (E+S)。

(4) Epidemic+自私节点+声誉 (E+S+R) 。在 Epidemic 路由算法背景下，我们将引入自私节点，并采用声誉激励机制，这是与 (E+S+BGI) 的不同之处。我们重点比较 E+S+BGI 和 E+S+R。

(5) Prophet算法+自私节点+BGI(P+S+BGI) 。与 E+S+BGI 不同，Prophet 算法被用作背景路由算法。我们希望展示 BGI 在不同路由算法中的性能。

(6) Prophet算法+自私节点+声誉 (P+S+R) 。Prophet 算法用于声誉激励机制。

理论上，在上述六种场景中，由于 E+N 中不存在自私节点，因此 EN 的性能是最好的，而 ES 可能是最差的，因为没有考虑对自私节点的激励。根据之前的分析，在 BGI 中，节点通过转发消息获得的奖励与公式(7)中的参数 $ b $ 有关，我们可以通过调整 $ b $ 的值来改变性能。需要注意的是，在 BGI 中，假设所有节点都是自私节点，每个节点都通过激励机制被激励参与消息传输。因此，自私节点数量与 E+S+BGI 的性能无关。

C. 仿真结果分析

如图2、3、4和5所示，当存在自私节点且没有激励机制时，投递率急剧下降，因为自私节点不参与消息传输。自私节点越多，投递率就越低。当自私节点数量为0时，意味着所有节点都参与消息传输，此时所有路由算法的性能几乎与普通 Epidemic 算法相同。当所有节点都成为自私节点时，即没有任何节点愿意帮助其他节点转发消息，消息仅从源节点直接传输到目的地节点，此时 Epidemic 和 Prophet 算法与直接路由算法类似。

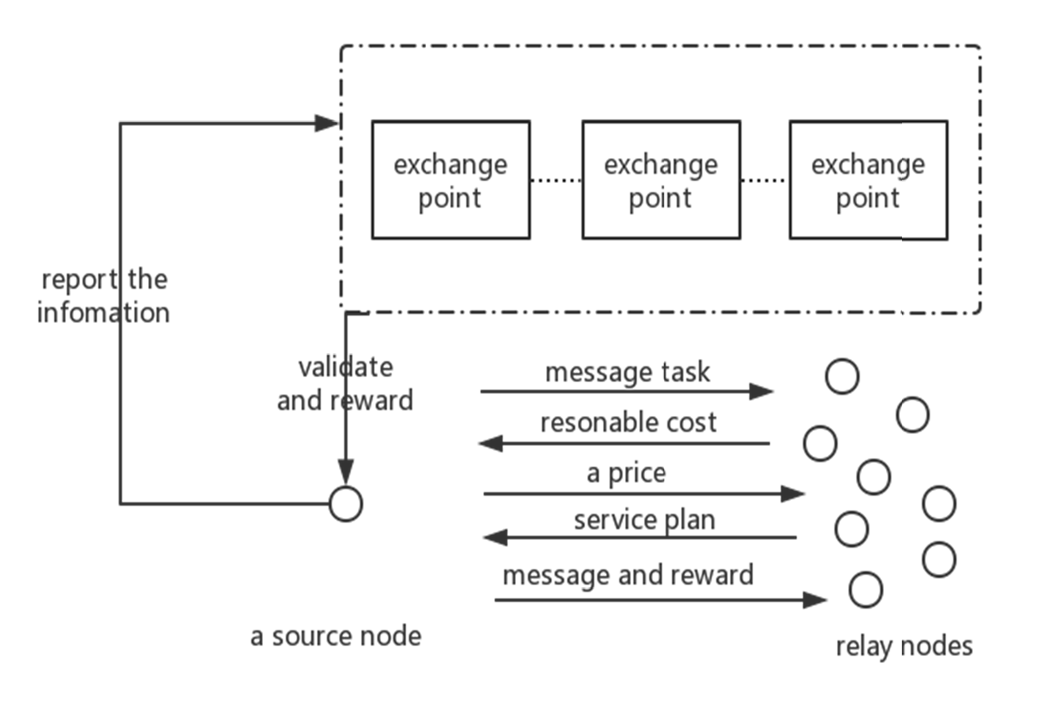
仿真结果表明，自私节点严重影响传输效率。如果加入所提出的激励机制，为了最大化收益，自私节点考虑与他人协作，因此投递率得到了显著提升。由于 E+N 中未考虑自私节点，E+N 的性能仅表示自私节点数量为零的情况。由于 E+S+BGI 将所有节点作为自私节点处理，因此 E+S+BGI 在不同数量的自私节点下具有相同的性能。

从图2、3、4和5可以看出，当网络中存在自私节点时，所提出的激励机制具有最高投递率，并且投递率与 E+N 几乎相同，表明该激励机制对自私节点的有效性。与 E+S+R 相比，E+S+BGI 的投递率平均提高 22.9%。与 P+S+R 相比，P+S+BGI 的投递率平均提高 26.5%。在路由算法方面，P+S+BGI 在 Epidemic 算法和 Prophet 算法中具有几乎相似的性能。

随着自私节点数量的增加，与开销相关的仿真结果如图6、7、8和9所示。由于自私节点不参与消息转发，E+S 和 P+S 中的开销比率随着自私节点数量的增加而降低。但在 E+S+R、P+S+R、E+S+BGI 和 P+S+BGI 中，自私节点为了最大化其收益而参与消息转发，因此随着考虑的自私节点数量增多，开销比率将上升。

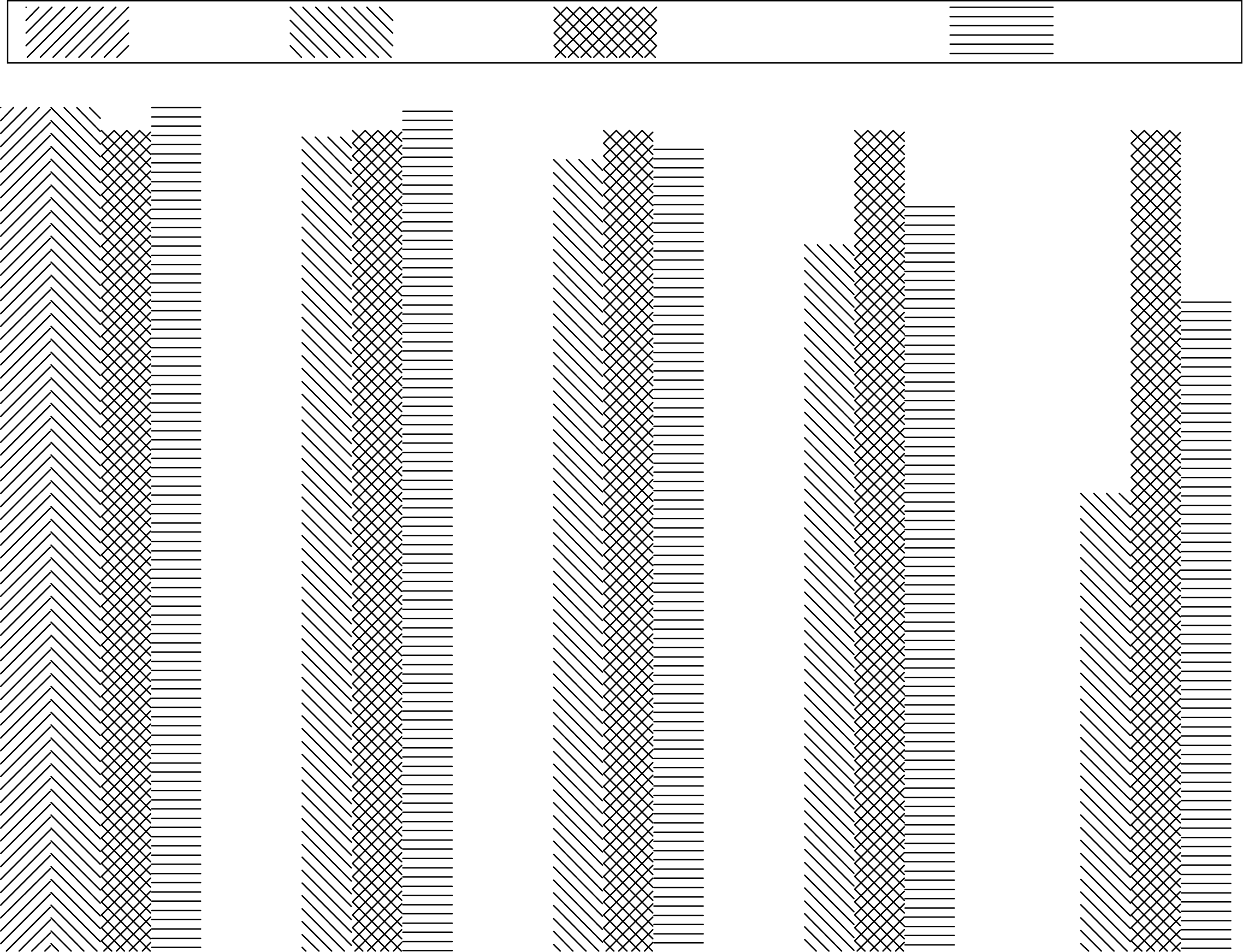
随着自私节点数量的增加，不同算法的平均延迟如图10、11、12和13所示。在机会网络中，参与消息转发的节点越多，从源节点到目的地的消息投递所需延迟越小。从仿真结果可以看出，由于本文提出的机制能够激励自私节点为其他节点转发消息，因此其平均延迟小于 E+S 和 E+S+R。与 E+S 和 E+S+R 相比，本文提出的机制平均延迟分别降低了 11.6% 和 9.2%。与 P+S 和 P+S+R 相比，本文提出的机制平均延迟分别降低了 8.5% 和 6.8%。必须注意到，采用基于 BGI 的激励机制后，平均延迟几乎与未考虑自私节点时的 E+N 或 P+N 相同。

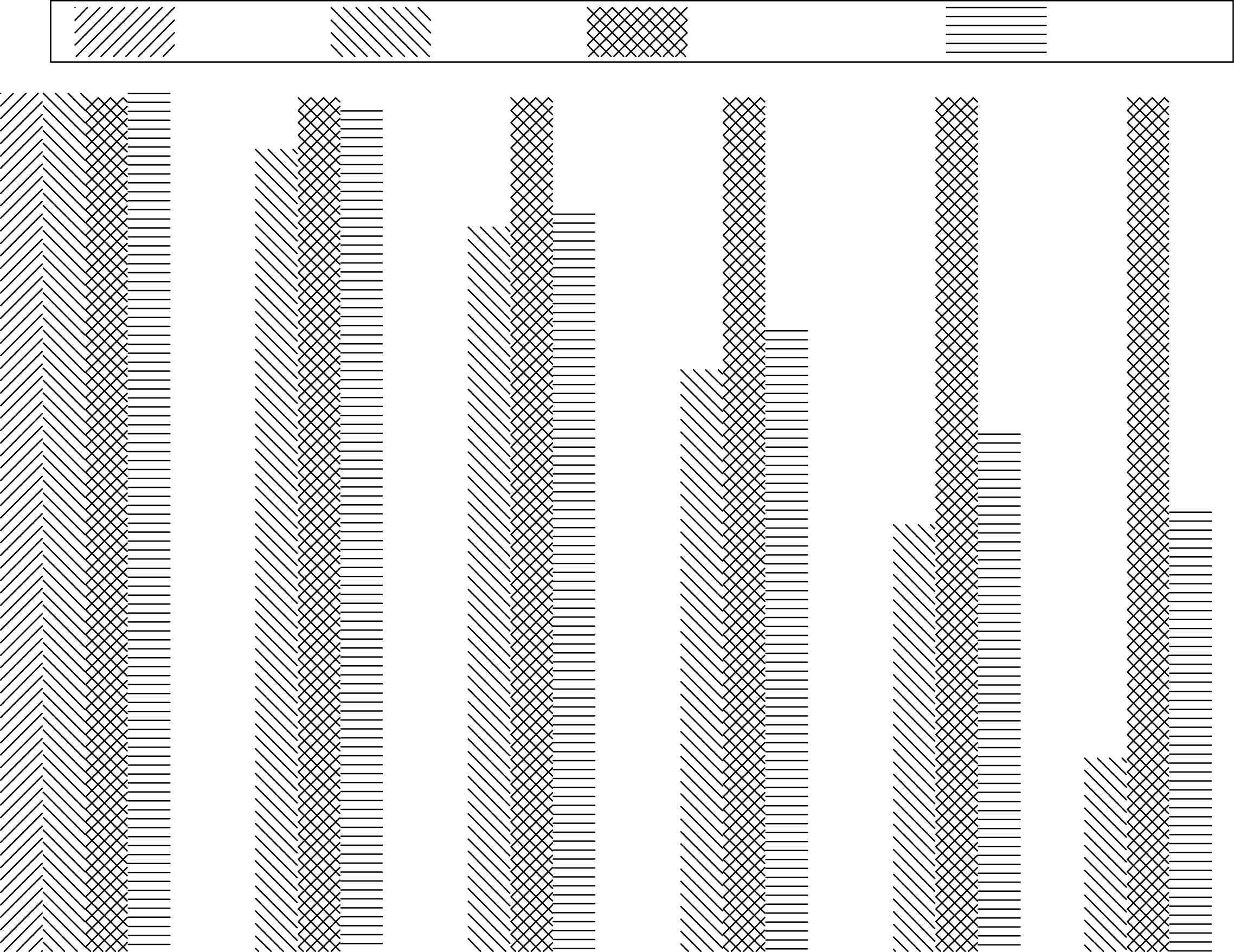
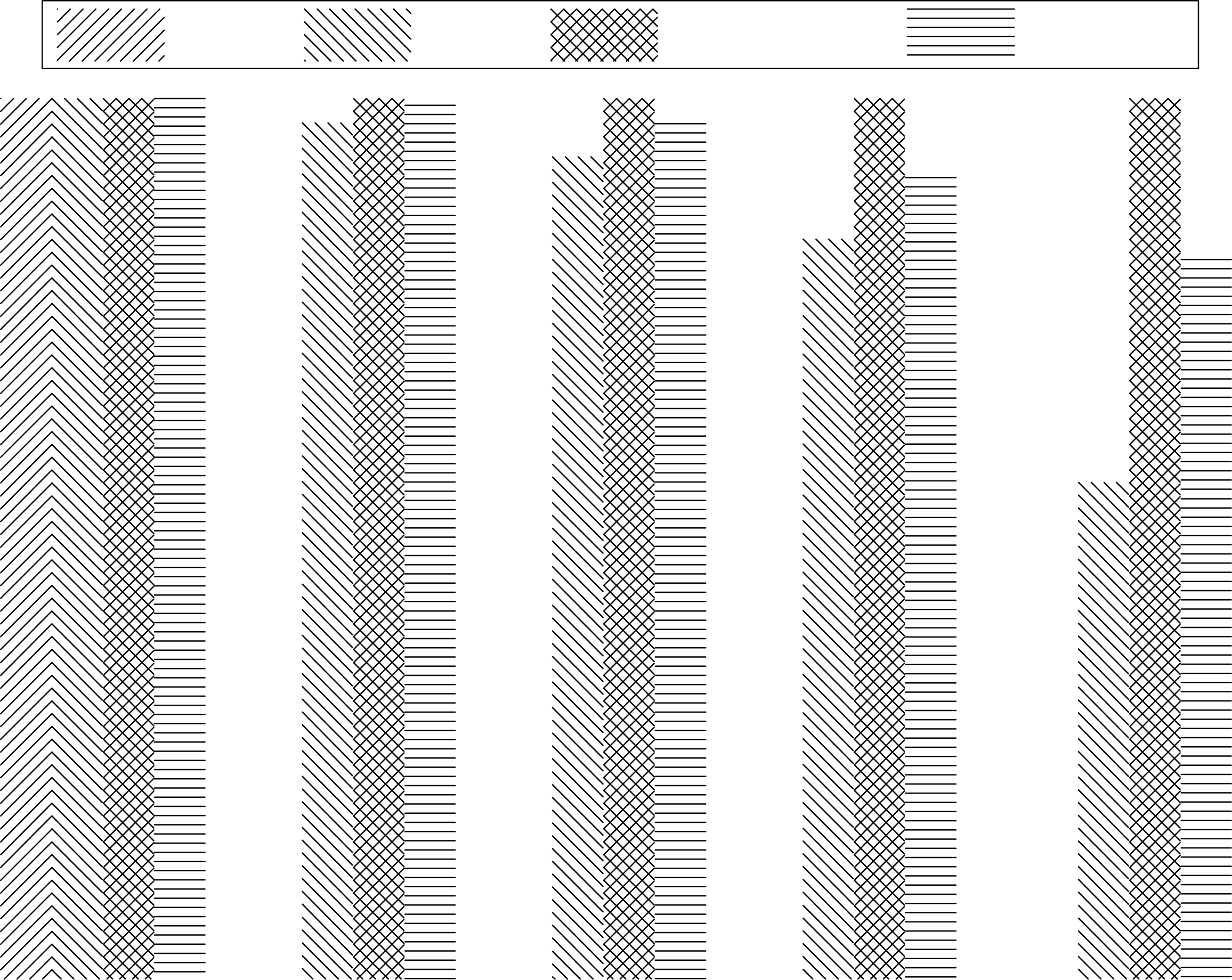
由于节点是理性的，所有节点只有在获得奖励时才会参与消息传输。因此，每个节点都希望最大化其效用。但是，每个节点都需要为消息接收和转发支付成本，在给定消息传输价格的情况下，每个节点都有最优的消息转发数量。从公式（7）可以看出，通过改变参数 $ b $ 的值，可以调整每个节点的消息转发最优数量。如果最优消息数量小于源节点希望转发的消息数量，则部分消息将被中继节点拒绝转发，从而可能导致消息传输的成功率下降。在图14、15和16中，我们展示了仿真结果，以显示参数 $ b $ 对 BGI 性能的影响。

从图14、15和16可以看出，当参数 $ b $ 取适当值时，E+S+BGI 的性能可以与 E+N 相同。在上述图表中，消息投递率和开销比率下降随着 $ b $ 的增加，平均延迟也随着 $ b $ 的增加而增加。在我们看来，较小的 $ b $ 会使节点转发更多的消息，这有利于消息传输，从而提高投递率并降低平均延迟。然而，更多的消息转发意味着网络的开销更高。如果 $ b $ 等于 0.1，E+S+BGI 与 E+N 具有相同的消息投递率和平均延迟，但开销高于 E+N。当 $ b $ 小于 0.1 时，性能没有变化，因为此时每个节点都会为其他节点转发所有消息。

六、结论

本文中，我们定义了源节点与中继节点之间的交互步骤：源节点决定中继节点转发消息的价格，而中继节点则根据给定的价格决定转发消息的数量。由于源节点和中继节点都希望最大化各自的效用，因此二者之间存在博弈关系。为此，我们将源节点与中继节点之间的协作建模为伯特兰德博弈，并提出一种激励机制以促进节点间的协作。为了最大程度地激励参与者，我们为参与消息传输的每个节点提供两阶段激励，即节点在接收和转发消息时均可获得奖励。对于源节点而言，其可通过交换点在转发消息时获得奖励；对于中继节点而言，其接收消息的奖励直接来自源节点。我们定义了源节点和中继节点的效用函数，并计算了它们的最优策略。基于博弈论分析，我们发现该博弈存在唯一纳什均衡。仿真结果表明，所提出的激励机制能够有效激励自私节点间的协作，提升路由算法在投递率和延迟方面的性能。与基于信誉的激励机制相比，所提出的机制 BGI 具有更优的性能，能够激励所有节点参与消息传输。当参数 $ b $ 设置为适当值时，采用 BGI 的机会网络可达到与不考虑自私节点的网络相同的性能水平。