基于涡流分析的溶血预测模型

评估医疗器械中湍流对血液损伤的一种方法

引言

为了有效设计人工心脏装置（如人工心脏瓣膜和心室辅助装置），需要确定流动场参数对机械性红细胞（RBC）损伤的潜在影响。在这些装置中，血液可能暴露于非生理流动条件，例如湍流性血流[1,2]，其设计依赖于确定湍流应力对红细胞的影响[3–5]。由于湍流具有混沌性和多尺度特性，可能导致血液中出现强烈的涡量以及局部高剪切应力和压力波动，通常被认为对红细胞损伤和溶血有显著影响。尽管红细胞暴露于湍流应力会增加溶血[5]，但血细胞附近具体的湍流特征及其导致细胞损伤的机制仍不明确[3–6]。

血液损伤通常由经验幂律模型表示，这些模型认为血液损伤是剪切应力大小以及血液暴露于高应力下暴露时间的函数。利弗里特等人[7]的这一观察结果导致了以下常用方程：

$$
HI = C s^a t^b \tag{1}
$$

其中，$ HI $ 为溶血指数（hemolysis index），用于衡量溶血程度，$ s $ 为剪切应力，$ t $ 为暴露时间（time of exposure）至应力 $ s $，$ a $、$ b $ 和 $ C $ 为需通过实验确定的常数。这些常数主要来自层流（laminar flow）数据，且基于明确的均质应力（homogeneous stress）和暴露时间（exposure time）条件。

如何最好地使用公式 (1)，甚至其对湍流的适用性尚不明确。将基于典型层流粘度计实验得出的幂律模型[7–10]应用于湍流存在问题。通过观察在特定几何结构、尺寸和运行速度下的扭矩，已从这些黏度计中获得近似均质剪切应力的实验测定结果。相比之下，湍流具有复杂结构，并伴随空间和时间相关的波动。细胞周围局部速度波动对溶血的综合影响，可能难以通过源自层流实验的模型来捕捉。因此，多位研究人员提出了修改幂律模型，或采用完全不同的模型和/或近似方法[11–20]。

流场中湍流动能的耗散可能决定了湍流对剪切流中红细胞（RBC）的影响[21]。最小的耗散性流动涡流由柯尔莫哥洛夫长度尺度（KLS）表征，其长度尺度定义为 $ KLS = (\nu^3/\varepsilon)^{1/4} $，其中 $ \nu $ 是流体的运动粘度，$ \varepsilon $ 是湍流动能的耗散率。湍流涡旋的耗散机制被称为能量级联[22,23]，其中大涡流不断破裂，并将其能量传递给更小的涡旋。因此，通过研究最小湍流涡旋的信息，可能获得湍流涡旋尺寸与红细胞损伤之间的关系，因为在能量级联的末端，如果最小的涡流尺寸与红细胞相当，它们可能通过应力与细胞相互作用，导致膜破裂和溶血。然而，如果涡流大于红细胞，则细胞很可能在流场中发生位移，细胞膜不会承受高应力或受损。一些研究人员已经考察了流动涡流尺寸相对于红细胞（RBCs）尺寸的关系，以确定导致红细胞损伤的机制[3,24–26]，并提出当KLS尺寸较小，特别是与红细胞尺寸相近时，红细胞将受到更大的损伤[2,3,25,27–29]。

在本研究中，我们基于三种截然不同设备的实验结果提出了一种溶血模型：射流[28]，库埃特粘度计[30]，和毛细管[5]。我们通过一种称为涡流分析的方法，利用KLS的时间平均空间分布来近似涡流表面积，研究溶血与涡流表面积之间的关系。本研究也是对我们前期研究的验证[31]，其中我们将该方法应用于库埃特粘度计[30]和毛细管[5]。我们假设溶血与具有足够能量的涡流表面积相关，这些能量可耗散到细胞膜上并导致细胞损伤。通过这种方式，可以在湍流流域内基于能量强度的广延性质（涡流表面积）来考察溶血。我们方法中的主要假设包括：(a) 假设KLS对应于半径等于KLS的球形涡流；(b) 显示特定KLS的整个流域体积均被直径等于KLS的球形涡流占据；(c) 流体为牛顿流体且均质；(d) 均质流体的湍流强度空间分布和大小能够反映血液的情况；以及 (e) k–ε 和 k–ω 剪切应力输运（SST）湍流模型适用于本文所考察的流动构型。基于这些假设，我们将来自文献的射流实验的实验性溶血数据与基于计算流体力学（CFD）模拟的涡流分析相结合，提出流动场中湍流涡流的广延度量可能是创伤的预测指标。我们展示了涡流分布与KLS之间的关系、涡流面积对溶血的影响，以及提出的溶血模型。

方法

建模系统

所建模的实验几何结构是由福斯特罗姆实现的轴对称射流[28]。该研究工作常被同样进行射流实验的研究人员引用。射流可在短暴露时间内产生高应力，类似于假体装置中的典型流动条件。福斯特罗姆的实验装置包括液体注射器、针头（射流）、血液注射器、液压缸组件和速度测量装置（更多信息见参考文献[28]）。射流发生在针头出口进入液体注射器的过程中，并在其中进行溶血测量。因此，本研究仅对针头和液体注射器进行了建模，同时采用了代表实际射流实验环境的条件，如参考文献[28]所述。这些条件包括几何结构（尺寸、直径等）以及流体性质和流动条件。针头的直径和长度分别为0.0346 cm和2.54 cm，注射器的直径为1.9 cm，长度为2.93 cm。通过针头将生理盐水注入充满人血的液体注射器中，人血用等渗盐水稀释至血细胞比容为8%，在15.22至39.03 m/s的不同速度下（见表1）。溶血在暴露时间为 $ 10^{-5} $ s的条件下测定。

计算程序

计算网格

使用 FLUENT14.0 及其预处理软件 ICEM CFD (Ansys, 宾夕法尼亚州匹兹堡) 对几何结构进行网格划分。重建了针头和注射器的三维模型。在创建几何结构后，使用六面体单元对整个几何结构进行网格划分。此外，通过在入口和出口区域周围使用O型网格，提高了针头和注射器的单元正交性和网格质量。在ICEM CFD中完成网格生成后，将流场几何结构导入 FLUENT 以求解不可压缩纳维‐斯托克斯方程。

流动模拟

模拟使用基于有限体积法的 FLUENT 模拟器进行。射流的边界条件包括在计算域入口处设置速度入口，以及在壁面上应用无滑移边界条件。求解参数设定为：采用二阶迎风离散格式、压力标准插值格式，以及用于压力‐速度耦合的 SIMPLE 算法。模拟开始时，指定较低的流体速度（使流动保持层流状态）作为入口速度。待模拟达到收敛后，在计算机中逐步提高速度，直至达到福斯特罗姆[28]实验报告中的某一实验速度值。当速度升高至足以产生湍流时，启用 k–ω SST 湍流模型。湍流模型的选择（k–ε 或 k–ω SST）依据模拟结果与理论预测的对比（详见下文）。重复此增速过程，直到完成对福斯特罗姆[28]实验中全部13种不同速度值情况（15.22–39.03 m/s）的模拟（表1）。所有射流模拟中的流体属性均采用牛顿流体模型，黏度为0.001 Pa·s，密度为998 kg/m³。不同射流实验情况下的雷诺数（Re）按公式 $ Re = Ud/\nu $ 计算，其中 $ U $ 为平均速度，$ d $ 为射流直径，$ \nu $ 为流体的运动黏度。如表1所示，雷诺数范围从5241（最低速度15.22 m/s）变化到13,440（最高速度39.03 m/s）。由于这些雷诺数均高于射流流动通常公认的临界雷诺数范围2000–3000[32–36]，因此射流中的流动完全处于湍流状态。当残差降至 $ 1 \times 10^{-5} $ 以下时，认为模拟已收敛。

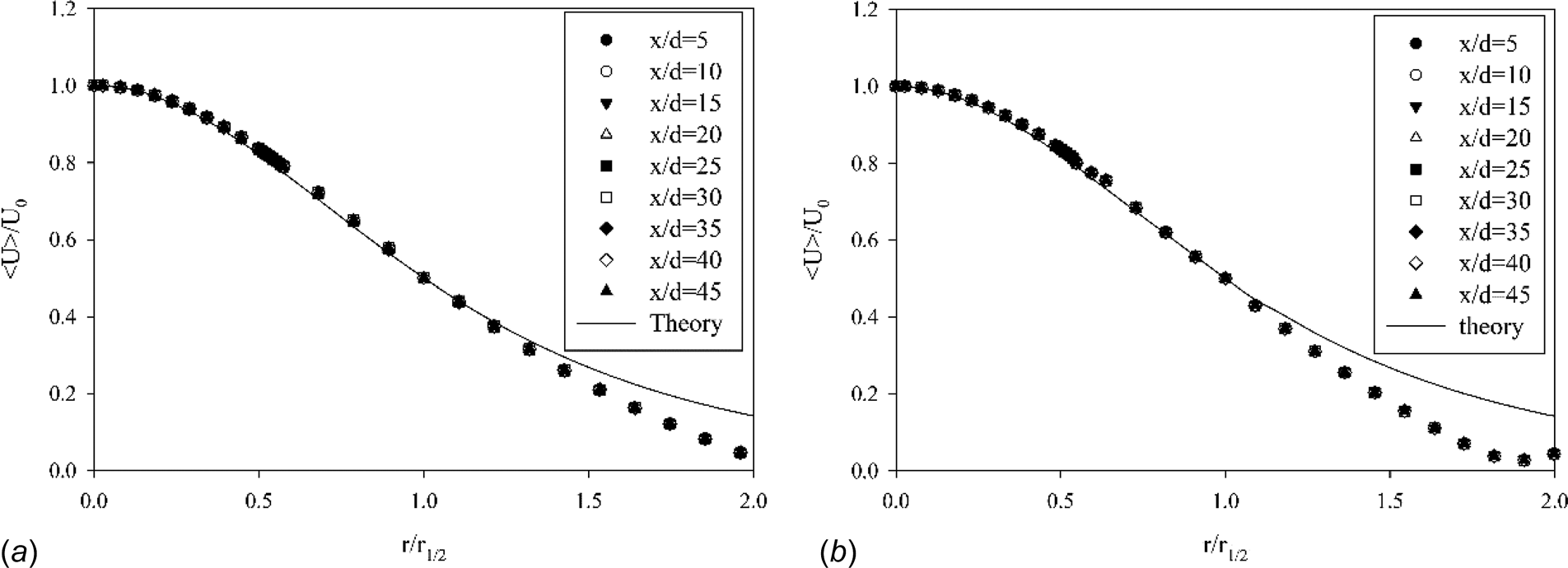
使用 k–ε 或 k–ω SST 模型，我们将模拟结果与理论预测进行了比较。通过对射流实验进行模拟，采用 k–ε 和 k–ω SST 湍流模型，并将模拟结果与理论预测的平均轴向速度 $ \langle U \rangle $ 分布以及湍流射流[37]的扩展率进行对比，从而完成对湍流模型的验证。为了比较平均轴向速度分布，在不同的 $ x/d $ 值下计算了中心线速度 $ U_0 $，和射流半宽 $ r_{1/2} $，其中 $ x $ 是从射流出口起算的轴向距离，$ d $ 为射流直径。当 $ \langle U \rangle / U_0 $ 的分布曲线以 $ r/r_{1/2} $ 为横坐标绘制时，在不同 $ x/d $ 区域的所有曲线应重合为一条曲线——即平均速度分布达到自相似[32]。图1中绘制了 k–ε 和 k–ω SST 湍流模型在不同 $ x/d $ 区域的平均速度分布。此外，还将模拟结果与理论[16]进行了比较。从图1可以看出，在流域计算中使用 k–ε 或 k–ω SST 模型并未产生显著差异，两种模型均在不同 $ x/d $ 位置表现出与理论一致的自相似性[32]。关于 k–ε 和 k–ω SST 湍流模型验证的更多细节可参见补充材料，该材料可获取。

涡流分析

对每种特定的实验射流流动条件进行了模拟，流体流动模拟生成了KLS的时间平均空间分布。沿射流轴线及其垂直方向创建了一系列垂直平面。这些平面与恒定KLS值曲面的交线界定了用于涡流分析的体积。

通过将分段计算域的平面间长度与由KLS等值线径向限定且以1微米增量划分的区域横截面积相乘，计算出包含相似球形尺寸耗散性涡旋的区域总体积。为了求得特定尺寸涡流的数量（$ N_{eddy} $），将该区域的总体积除以单个涡流体积（$ V_{eddy} $），其中单个涡流体积计算公式为 $ V_{eddy} = \frac{4}{3} \pi (KLS/2)^3 $。最后，针对每个KLS值的涡流总表面积（$ A_{eddy} $）计算为 $ A_{eddy} = N_{eddy} \cdot 4 \pi (KLS/2)^2 $。在计算出涡流总表面积和涡流数量后，通过除以溶血发生区域的总体积对结果进行归一化处理。

该归一化的目标是生成与设备无关的量，可用于比较不同的湍流情况和实验配置。先前的研究[31]表明更小的涡旋更具破坏性，因此我们使用了KLS ≤ 10 μm区域内总体积：目的是确定溶血与广延量而非强度量在不同KLS值下单位体积内的对应关系。此外，还考虑了这些广延量随KLS值增加的累积值。

结果与讨论

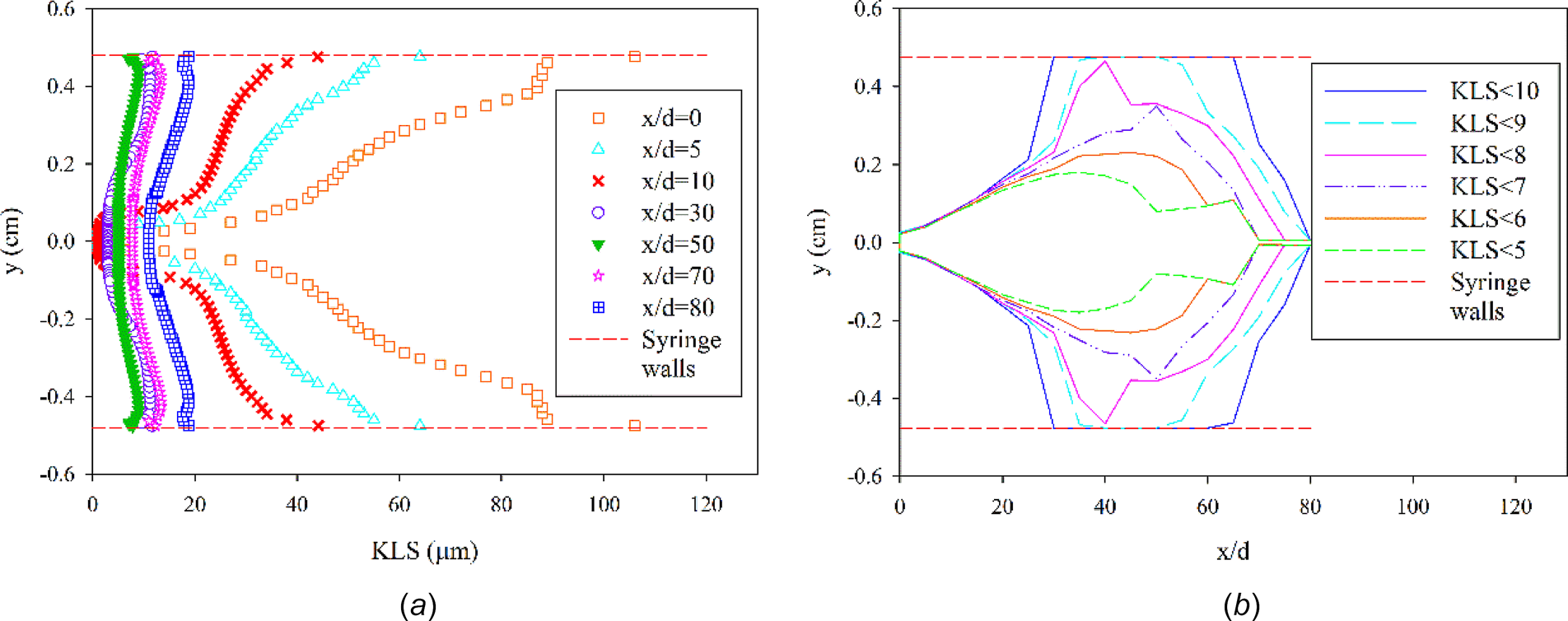
最高流速实验（39.03 m/s）的KLS值范围为1 μm至106 μm，而最低流速实验（15.22 m/s）的KLS最大值可达168 μm。完整的KLS范围及实验条件见表1。

最高流速实验中，从射流出口开始、在注射器不同轴向位置处的若干条线上的KLS值的时间平均空间分布（$ x/d = 0 $，其中 $ d $ 为针头内径）如图2(a)所示。由图2(a)可以看出，KLS值在径向和轴向上均有变化。在给定的轴向位置，较小的KLS值出现在中心线附近（$ y = 0 $）。此外，由于本研究认为较小KLS值（KLS ≤ 10 μm）会导致更严重的损伤，研究发现含有较小KLS值的区域（从KLS ≤ 5 μm到KLS ≤ 10 μm）存在（对于最高速度射流实验，该区域可见于图2(b)）。与低速实验相比，高速射流导致了更大范围的较小KLS值区域。该结果表明，更大范围的更小涡旋（KLS ≤ 10 μm）与更严重的溶血相关，因为最高速度射流实验表现出最高的溶血程度（表1）。

涡旋尺寸分布与溶血之间的关系

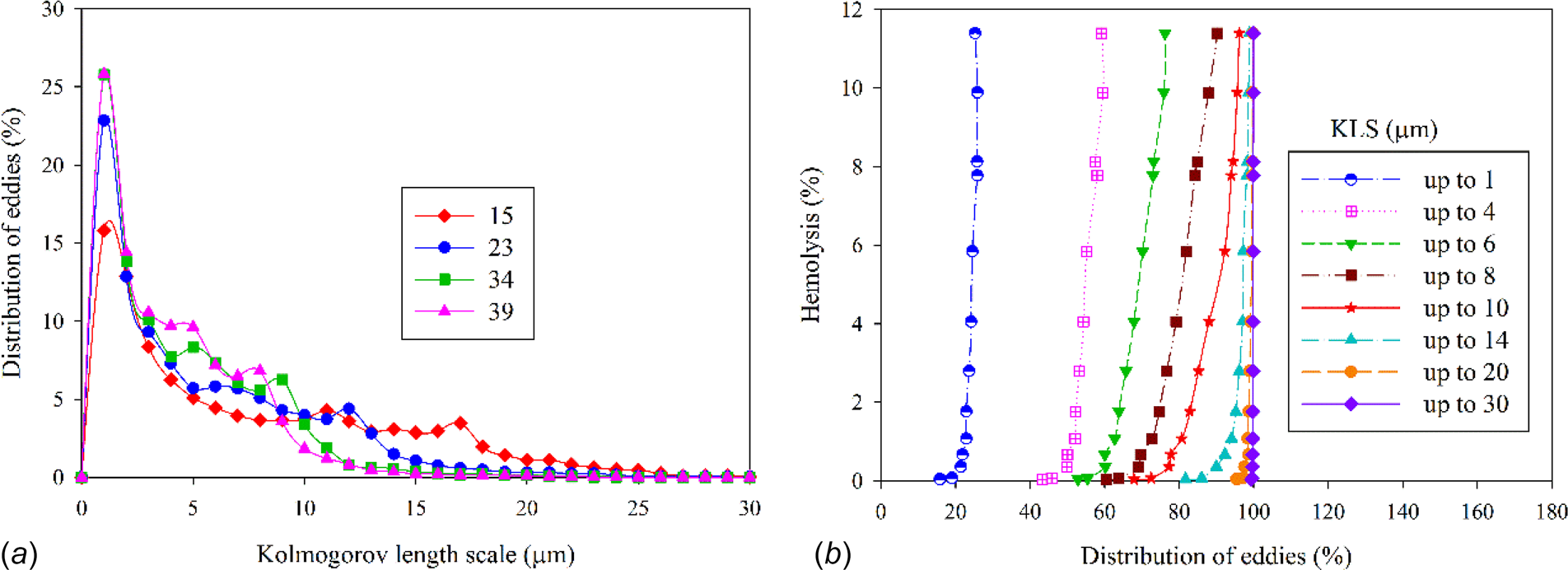
基于KLS值，计算了所有13项福斯特罗姆射流实验（表1）中耗散性涡旋的尺寸分布。这些涡旋尺寸分布在图3(a)中绘制（为简化起见，并未显示所有实验）。结果表明，在速度较高、溶血更多的实验中，更小的涡旋数量增加。尺寸分布也向更小的值偏移，模拟结果亦如此。

速度增加。还研究了涡流分布与溶血之间的关系。通过将特定KLS以下的涡流数量进行累加，并与实验测得的溶血数据一起绘制在图3(b)中。从图3(b)可以看出，当KLS在10 μm以内时，其对溶血的影响更为显著。超过该值后，影响变得不再重要（可通过观察较大KLS值时垂直的KLS曲线推断）。这一发现表明，湍流中的血液损伤可通过更深入探究科尔莫戈罗夫长度尺度的作用来预测，这与前人提出的方法一致。

涡流表面积对溶血的影响

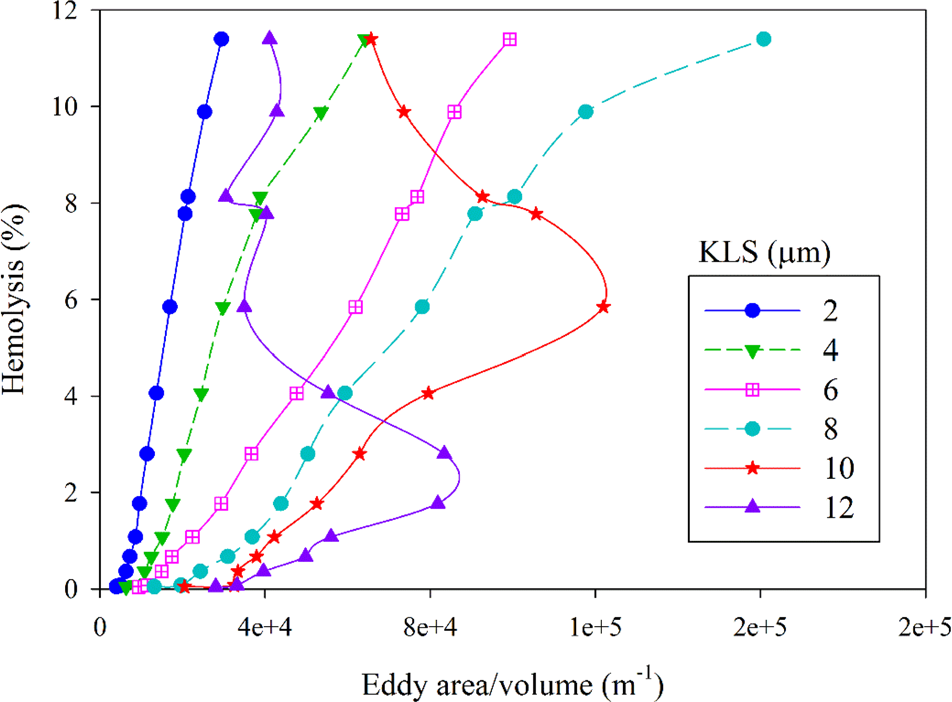
已针对射流中的13次实验，计算了不同KLS值下单位体积内KLS尺寸涡流的表面积。为进一步探究涡流面积与溶血之间的关系，将射流的实验结果与模拟数据进行了结合分析。图4展示了单位体积内的涡流表面积与溶血的关系曲线。分析以每1 μm的KLS值进行，但为清晰起见仅展示了奇数KLS值的结果。从图4可以看出，当KLS值从8变化到10 μm时，曲线形状发生变化。当KLS大于10 μm时，曲线回折向上，并在更大的KLS值时趋于垂直，表明在此流场中，此类涡流的存在与溶血之间无明显依赖关系。溶血与单位体积内涡流数量的关系图（此处未显示）也显示出与KLS相同的趋势。

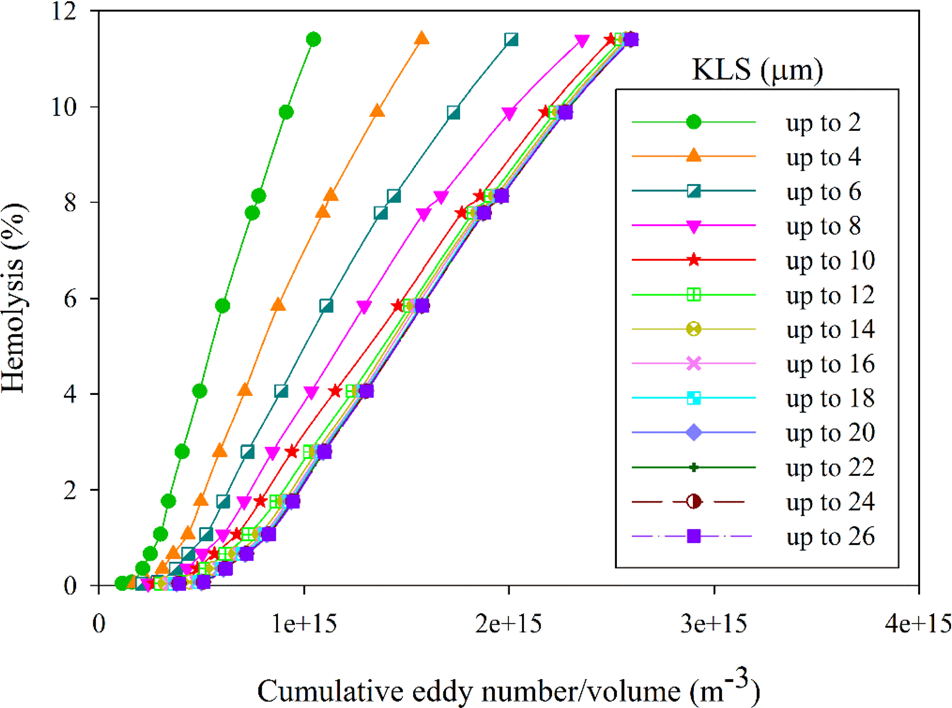
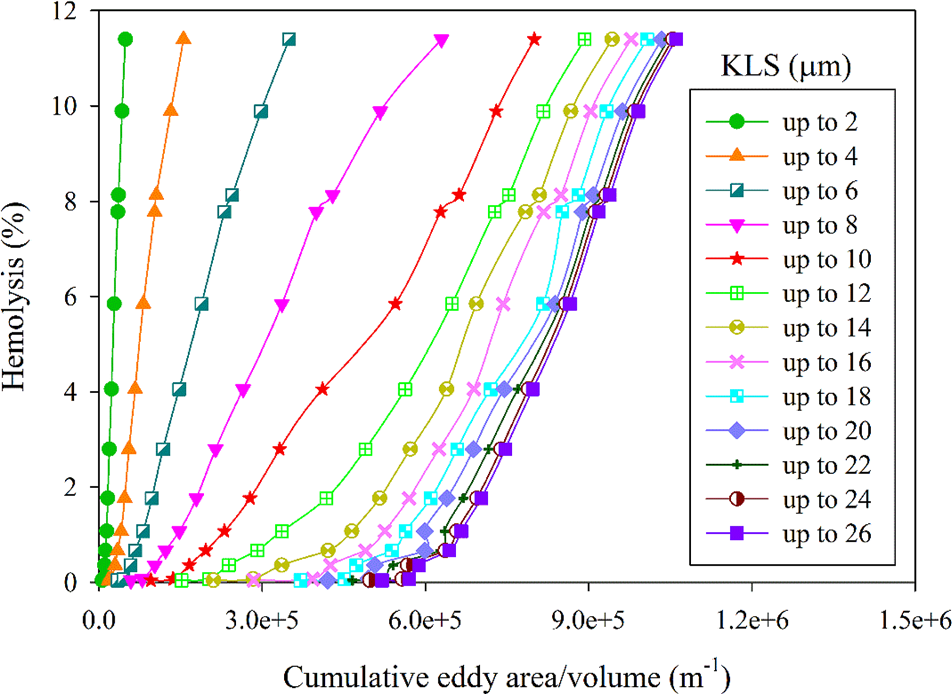
如图4所示，小于某一尺寸的涡流与溶血有关，射流实验的临界涡流尺寸约为10 μm。此外，还研究了累积涡流面积，该参数相较于将涡流面积按1 μm的KLS区间进行分组更能提供深入的理解。通过随着KLS值的增加累加KLS涡流表面积，考察了所有尺寸小于临界值的涡流的累积效应。图5展示了涡流表面积的累积和与%溶血之间的关系。从图5可以明显看出，随着单位体积内KLS涡流表面积的增加，溶血也随之增加。为清晰起见，仅显示了KLS值的偶数值。注意，对于较高KLS值，曲线开始相互重叠，特别是在KLS > 10 μm时。累积涡流数量与溶血的结果也类似（图6）。

图4–6表明，较小KLS值与溶血水平的变化相对应，而较高KLS值与溶血的相关性较弱或无相关性。该结果支持了我们的前期研究[31]，其中涡流分析被应用于两个不同的实验，即库埃特粘度计[30]和毛细管[5]。这三个实验的流场和暴露时间非常不同。射流实验的暴露时间为 $ 10^{-5} $ s，毛细管实验约为1 s，而库埃特粘度计实验为4 min。通过对三个不同系统进行涡流分析，发现临界KLS值约为10 μm，并且在涡流表面积与溶血、涡流数量与溶血之间观察到类似的关系。此处的分析可利用这三个系统的实验结果对溶血进行定量预测。

溶血模型进行了一系列测试，以找到适用于所有三个截然不同系统的最佳经验模型。在三个系统中使用了溶血率低于5%的实验数据，因为该模型在较低溶血水平下的改进可能最为有效。为了找到对这三个系统的最佳拟合，对不同函数进行了回归分析。尽管每种函数类型均分别使用涡流面积和涡流数量进行测试，但本文所呈现的结果均为基于涡流面积的拟合结果。使用涡流的表面积在物理意义上更为合理，因为细胞实际经历的是这些涡流的面积，而非涡流的数量。此外，针对每种函数类型，还分别对每个单独系统、任意两个系统的组合以及全部三个系统共同进行了回归分析。几种测试过的试验函数形式见表2。我们给出了三个系统最佳拟合的曲线图及相应的系数值。

从表2可以看出，我们还通过将涡流面积与不同的KLS尺寸组合进行分箱，测试了多个函数。对涡流面积进行如此分箱的原因是，三种系统（即射流、库埃特粘度计和毛细管）中的涡流尺寸分布差异很大，尤其是在射流实验中。因此，特定KLS尺寸的涡流面积在这些系统中的贡献可能各不相同。

在对这些函数类型进行测试未能得到令人满意的拟合结果后，我们考察了不同bin尺寸下以涡流面积（以及涡流数量，此处未展示）为变量的线性函数。我们还尝试了其他几种具有不同bin尺寸和不同系数数量的形式。在所测试的函数中，以下两个线性函数被认为是最优的：

$$
HI = b \cdot t + c \cdot EA_{KLS(0-4)} + d \cdot EA_{KLS(5-7)} + e \cdot EA_{KLS(8-10)} \tag{2}
$$

$$
\text{溶血指数} = a + b \cdot t + c \cdot EA_{KLS(0-3)} + d \cdot EA_{KLS(4-6)} + e \cdot EA_{KLS(7-9)} \tag{3}
$$

其中 $ HI $ 为溶血指数（%），$ t $ 为暴露时间，$ a $、$ b $、$ c $、$ d $ 和 $ e $ 为需通过实验确定的系数，$ EA_{KLS(R_1-R_2)} $ 为KLS尺寸从 $ R_1 $ 到 $ R_2 $ μm的单位体积累积涡流表面积。方程（2）和（3）中对应不同 $ R_2 $ 值的系数见表3。

我们还使用两个线性函数（公式(2)和(3)）对射流实验[28]，以及毛细管[5]和库埃特粘度计[30]实验进行了溶血计算。库埃特粘度计和毛细管的实验条件详情可参见我们的前期研究[31]以及实验结果的原始出版物。

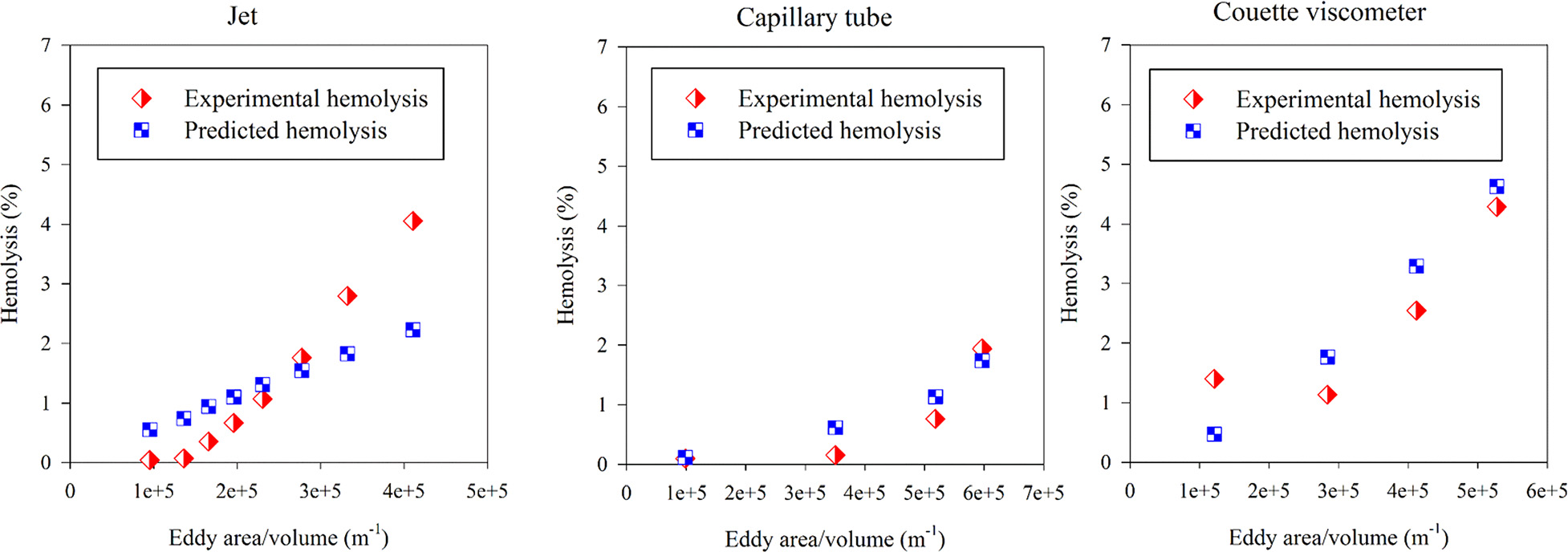
从图7可以看出，溶血模型（公式(2)）即使在不同实验条件下也与实验测得的溶血值表现出较为合理的一致性。其中，射流实验的结果一致性最差，因为其暴露时间（$ 10^{-5} $ s）远短于库埃特粘度计实验的240 s暴露时间，且KLS尺寸更小，两者相差达7个数量级。我们还分别对这三个系统使用公式(2)和(3)进行了拟合，得到了每个实验对应的系数，如表4所示。可以看出，不同设备之间的系数差异可达几个数量级。这表明了寻找一个通用的溶血模型存在一定挑战，但仍具有一定的价值。

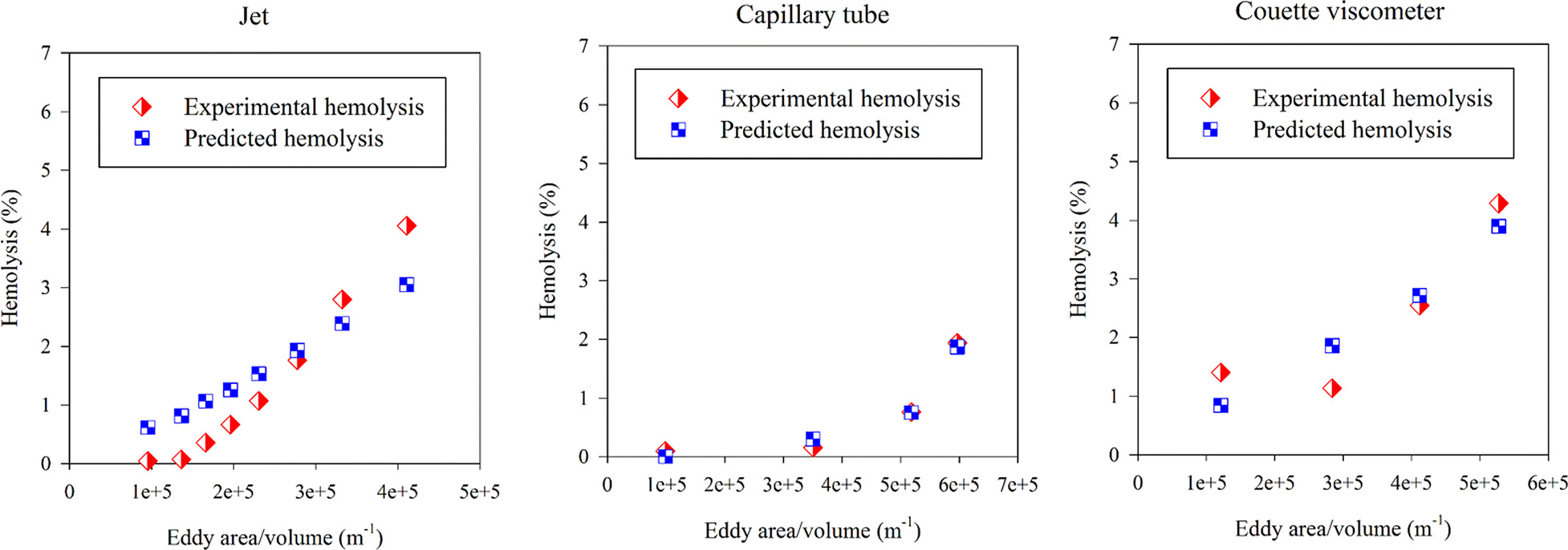
线性模型既可以分别拟合这三个系统，也可以在将数据合并考虑时进行拟合。利用表4中的系数代入公式(2)，对三个系统分别进行了溶血预测（图8）。图中出现的非线性是由于随着湍流增强，涡流尺寸分布向更小尺寸偏移所致。

这些结果表明，涡流分析在预测湍流引起的溶血方面具有一定前景，但仍存在明显需要探索的研究方向。涡流分析并不局限于柯尔莫哥洛夫理论，因此可以基于其他方法来估计长度尺度。此外，在考虑计算需求以及开展此类模拟的可行性的同时，还应考虑使用比雷诺平均纳维‐斯托克斯更复杂的模拟技术来模拟湍流。另外，应致力于获取更多生理学上和临床上相关数据并进行分析。

结论

从层流实验中推导出的模型（例如幂律型模型）不足以捕捉湍流的复杂性。本研究针对射流考察了湍流特性与溶血之间的关系。结果表明，溶血与直径达约10 μm的柯尔莫哥洛夫尺度涡流的总表面积之间存在明显关联，而对于较大的涡流则未表现出明显关系。该结果支持了我们前期研究[31]，其中分析了两个截然不同的实验：库埃特粘度计[30]和毛细管[5]。对于这三个截然不同的系统，模拟均显示出溶血对较小KLS的涡流面积具有明显的依赖性，而当KLS接近10 μm时，这种依赖性似乎减弱或消失。尽管10 μm的涡流尺寸阈值在某种程度上是任意的，但较小的涡旋反映出更高的湍流强度，因而导致细胞损伤的可能性更大，这一推断似乎是合理的。

提出了一种新的模型来预测湍流中的溶血，该模型通过赋予不同尺寸涡流不同的权重，考虑了湍流的复杂性。提出的溶血模型仅在完全湍流区域中严格有效。将溶血视为涡流表面积的函数，可建立与流动的广延性质之间的关系——这种方法更适合于解释医疗器械中流动的复杂性。设备中的小而高度湍流区域可能对溶血产生显著影响，且该区域的大小对损伤程度至关重要。该模型还被应用于库埃特粘度计和毛细管的实验结果。

对于这三个截然不同实验的流场和暴露时间，已获得合理的一致性。这些实验之间的差异，例如血细胞比容，会影响细胞所受应力的水平，因为它是血液黏度的决定因素。我们使用现有文献数据中关于较低血细胞比容下湍流溶血的数据开发了这一方法。尽管我们认为涡流分析在差异极大的系统中表现已相当出色，但预计未来的研究若能考虑临床相关血细胞比容及其他可能因素，该方法还可进一步改进。此外，还需要更多的实验数据来发展基于涡流分析方法的模型，以使其具有更广泛的适用性。

此处提出的涡流分析和溶血模型可与各种湍流模拟结合使用，似乎适用于广泛的不同条件和医疗器械。对柯尔莫哥洛夫涡流尺寸分布的预测，可能有助于评估某种医疗器械设计在多大程度上容易发生溶血，以及需要在设计上做出哪些改进以增大柯尔莫哥洛夫尺度。如果要将涡流分析应用于更广泛的范围，在应用中，需要针对不同的KLS值，在暴露时间的函数关系下对湍流中的溶血进行额外测量，理想情况下应在KLS值接近均匀的流场中进行。