计数排序法

        计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。 当然这是一种牺牲空间换取时间的做法。

        其基本原理是：统计待排序数组中每个元素出现的次数，然后按顺序记录这些次数，并最终输出此序列。计数排序至少有数组完成，其中A数组代表了待排序的数据，B数组是临时数组，用来存放各个元素的个数。通过收集的B数组的数据，再对A数组进行重新复制，从而产生有序序列。

        动图模拟如下：

 

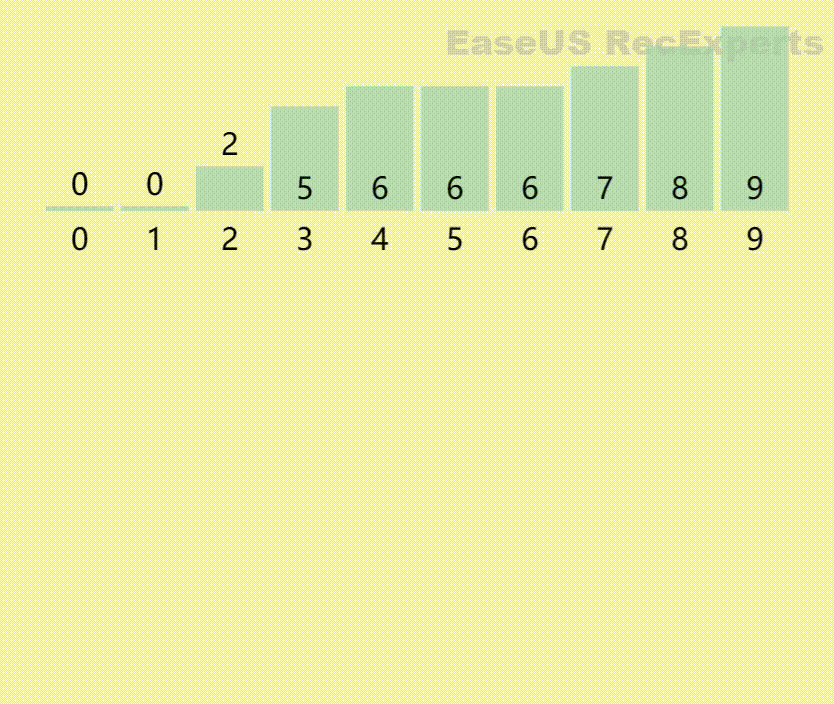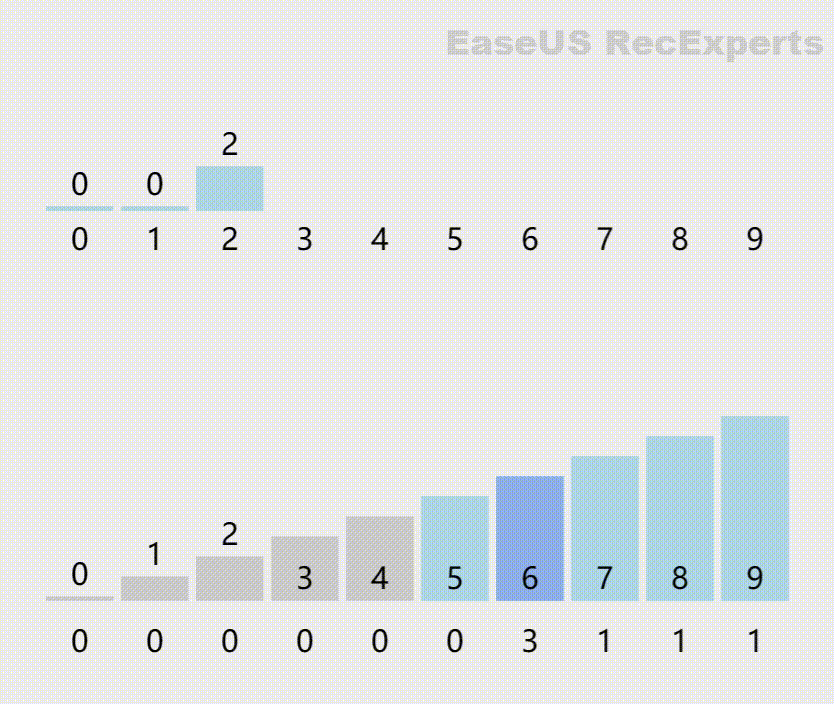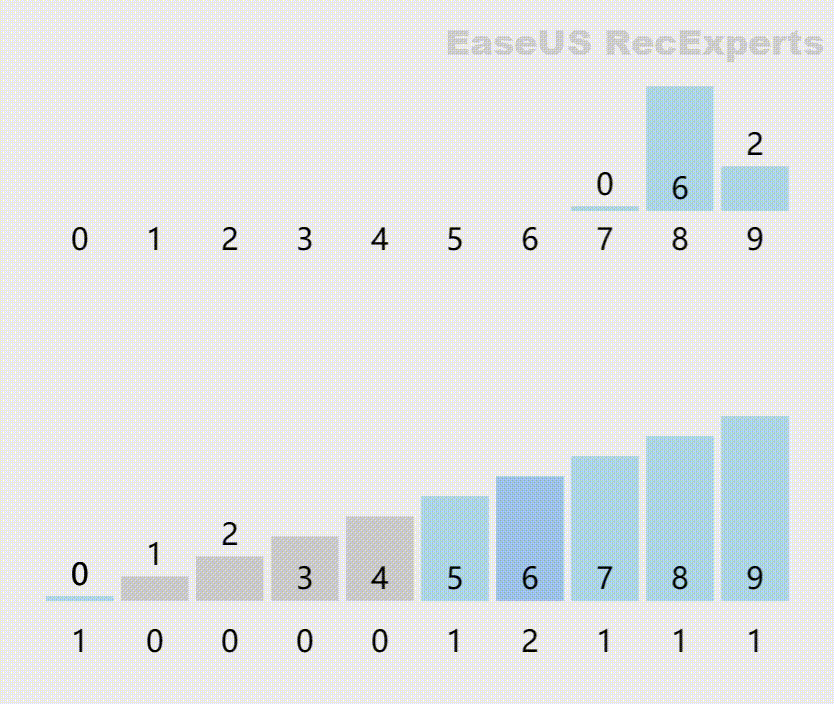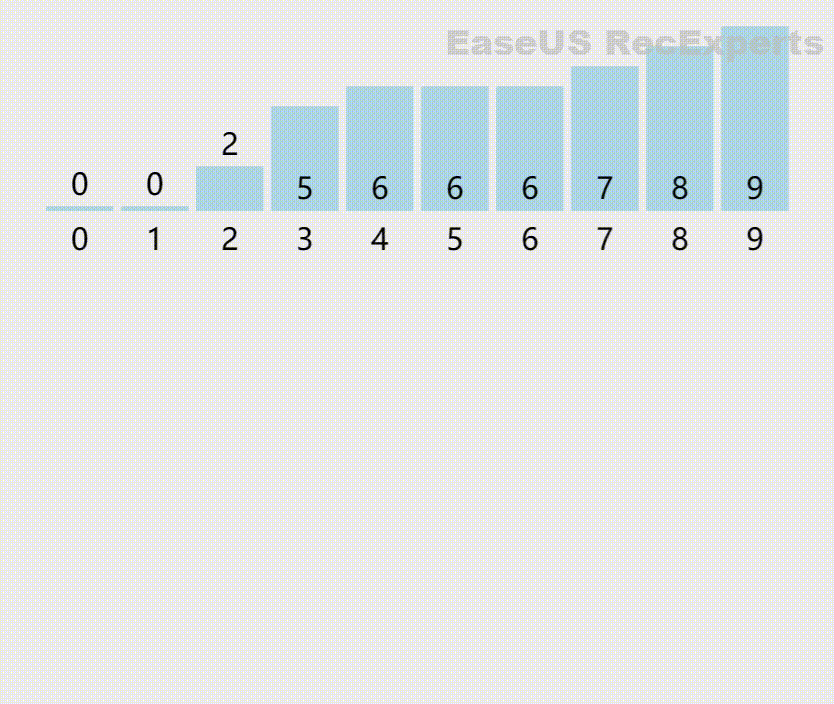
具体C语言代码如下：

#include <bits/stdc++.h>
using namespace std;
void CoutSort(int *num,int len); 
int main()
{
	int num[10]={34,8,2,3,78,56,16,90,48,2};
	CoutSort(num,10);
	for(int i=0;i<10;i++){
		cout<<num[i]<<" ";
	}
} 

void CoutSort(int *num,int len)
{
	if(len<2){//如果只有一个数就直接返回不用排序 
		return;
	}
	
	int i,j,max=0;
	for(i=0;i<len;i++){
		if(max<num[i]){
			max=num[i];//求出数组中最大的数 
		}
	}
	
	int tem[max+1];//定义的存每个数出现几次的数组 
	memset(tem,0,sizeof(tem));//初始化这个数组 
	for(i=0;i<len;i++){
		tem[num[i]]++;//存入每个数出现几次 
	}
	
	int k=0;
	for(i=0;i<=max;i++){
		for(j=1;j<=tem[i];j++){
			num[k]=i;//把计好的数在重新写入数组 
			k++;
		}
	}
}

 总结：

1. 算法名称：计数排序（Counting Sort）

2. 算法类型：非比较型整数排序算法

3. 算法原理：统计待排序数组中每个元素出现的次数，再按顺序依次输出。

4. 算法时间复杂度：O(n+k)，其中n是待排序数组的长度，k是待排序数组的最大值与最小值之差加上1。

5. 算法空间复杂度：O(n+k)，需要一个额外的数组C来存储每个元素出现的次数。

6. 算法稳定性：计数排序是一种稳定的排序算法，相同的元素在排序后会保持原有的相对顺序。

7. 算法应用场景：计数排序适用于待排序数据是有固定范围的整数的情况，例如年龄、考试成绩等。

8. 算法局限性：计数排序对于含有负数或者浮点数的数据不适用，且当待排序数据的取值范围很大时，需要占用较大的额外空间。