基于上车控制的多公交调度

基于上车控制的多公交调度策略

摘要

本文针对环形道路公交运输系统提出了一种多公交调度策略，该策略支持单辆公交车或多辆公交车的调度，并考虑了公交车和车站的客流量动态。此外，首次将乘客感知等待时间作为成本函数的一部分进行建模，以考虑乘客焦虑，从而提升公交运营的服务质量。在上游站点，尽可能多的乘客上车，导致车内剩余空间减少，进而延长下游站点乘客的等待时间。为避免此类现象，在乘客上车过程中引入公交上车控制，并通过同步加载模型为下游车站的候车乘客提供上车机会。所建立的问题在两种不同场景下进行求解：线性成本和非线性成本。线性成本包含乘客实际等待时间和公交车利用率，首先将其转化为混合整数线性规划（MILP）问题，并利用商业求解器 Gurobi求解。考虑到计算复杂度，还采用了两种不同的进化算法——遗传算法（GA）和和声搜索算法（HS），以实现实时求解。在场景2中，非线性成本结合了乘客感知等待时间和公交车利用率，直接由GA和HS进行求解。最后，通过案例研究验证所提策略的有效性，与传统公交调度策略进行比较，并分析当考虑乘客实际等待时间或乘客感知等待时间时，公交车载客过程的不同影响。

索引词

公共交通系统，公交调度，公交停站时间，遗传算法。

一、引言

PUBLIC 由于其在经济效率和社会公平性方面具有较大的客流量和可持续性，交通运输[17]已研究多年。然而，这种随机性乘客需求的变化和沿途交通状况使得准点公交车到达难以保障。即使日常通勤者的出行模式可以被掌握，一些特殊事件仍会显著增加公交运营的复杂性，例如大型流行音乐会和重大道路交通事故。鉴于此，过去几十年中提出了许多运营策略[13]。

一种典型的方法是为运营公交线路选择合适的公交发车频率，以吸引更多乘客，同时降低运营成本。纽厄尔通过建立一个解析模型建议，发车频率应大致与乘客到达率的平方根成正比[25]，但这基于一个不切实际的假设，即车辆容量足够大，能够容纳所有候车乘客。另一种方法基于塞德尔提出的数据收集方法[1],[2]，其中讨论并比较了两种不同的检查方法。第一种是通过每日或每小时最大乘客载荷点进行的点检法，第二种是通过原始或调整后的负载曲线进行的乘车检查法：当提供相对平坦的数据曲线时，应采用点检法，否则乘车检查法更为合适。此外，还开发了许多数学优化模型，旨在最小化乘客等待时间或运营成本。韩和威尔逊[16]提出了一个与公共交通路线选择相结合的频率设定问题，该问题在车队规模和装载可行性等约束条件下，最小化乘客等待时间和公交车拥挤程度。随后，韦尔巴斯和马赫马萨尼将其扩展并表述为一个非线性规划问题[33]，并在大型城市网络上实施，以研究乘客弹性异质性的影响[34]。然而，所有这些模型都是基于交通分配模型开发的，未考虑详细动态，例如公交车流量动态和站点流量动态。而对于考虑单走廊公交线路客流量动态的研究[7],[8],[28]，研究人员关注的是公交车道路运行，而不考虑公交调度，后者在论文中被假定为已知。

除了通过提出公交频率问题来调整时刻表间隔外，还提出了自适应公交车规模控制以帮助改善公交运营服务。奥尔德菲尔德和布莱提出了一种数学模型来研究运营成本与最优公交车大小之间的关系，他们发现公交车大小的增加也会导致运营成本增加[26]。史蒂文提出了一种优化模型，通过优化发车间隔、车辆大小和路线选择来最小化乘客等待成本和公交运营成本，然而该模型未考虑公交载客量、公交运行动态和站点动态，并假设乘客到达率为固定参数[19]。此外，亏量函数被用于确定满足预设时刻表所需的最少公交车数量[3]。不同类型的公交车及其不同的车辆大小也被应用于多车场或公交走廊问题中[9],[20]。同时，塞德尔et al.尝试调度不同类型和尺寸的公交车，以实现均匀的发车间隔和均衡的载客量[4]。孙 et al.提出一种优化模型，通过调度混合尺寸的公交车和不均匀发车间隔，以最小化乘客等待成本和公交运营成本[30]，但该模型因缺乏对公交载客量和站点动态的描述而变得不切实际。

公共交通问题涉及许多不同的目标，例如最小化乘客等待时间和运营成本、最大化多条公交线路的协同性、保持发车间隔一致性。关于乘客等待时间，大多数优化模型关注的是最小化实际乘客等待时间，却忽视了乘客心理感知的影响，而心理感知与人性化服务质量直接相关。正如所说：“时间既可以客观衡量，也可以主观感知”[12]。时钟上显示的时间是从客观视角来看的实际时间，而时间也可以基于用户的感觉被感知，这种感知受到多种因素的影响，例如公交车不准时到站、设施布置、服务信息等[6],[24],[37]。对等待时间的感知显著影响用户体验，从而影响乘客的出行方式选择[11],[29],[35]。因此，为了建设以公共交通为导向的环保型城市，必须考虑用户的个人感知。

鉴于当前情况，本文首先提出了一种考虑站点需求动态和公交需求动态的环线路公交线路多公交调度策略。由于高科技传感器的改进和应用，先进公交系统已在全世界范围内实施[10]。公交车在专用公交道上运行，配备支持GPS的路线控制器和数字摄像机以收集实时信息，从而显著降低了这些智能交通系统中的不确定性[23]。因此，本文重点研究公交调度与车站控制，旨在满足乘客出行需求的同时降低公交运营成本。具体而言，首先建立了考虑站点需求动态和公交需求动态的环线路公交线路混合逻辑动态模型。在本模型中，公交场站为每个班次派遣单辆公交车或公交车队，提供可变公交规模以满足沿线的随机乘客需求。乘客感知等待时间首次被建模为一个非线性函数，用于描述在预期公交车到达时间之后仍未上车乘客的不满程度。该问题通过混合整数线性规划求解器以及进化算法（遗传算法GA和和声搜索算法HS）进行求解。此外，我们将所提出的方法与传统的固定时刻表和优化的单车调度方案进行比较，以说明本方法的有效性，并讨论采用线性等待时间和感知等待时间各自的影响。

本文组织如下。第二节介绍了公交调度模型的具体描述。第三节给出了求解优化问题的算法。第四节描述了仿真结果。第五节得出了结论。

II. 公交调度问题的建模

本文中的公交线路形成一个环形道路，如图1所示，调度的公交车从终点站出发，最终返回同一终点站。同时，终点站可以为每个班次派遣单辆或多辆公交车。本文中的班次k与时间k具有相同含义，每个班次k可以派遣一辆公交车、多辆公交车，甚至不派遣公交车。如果一组公交车同时从终点站发出，则称该组为车队platoon，其中每辆公交车被称为被分配assigned至同一班次。同一班次中的公交车将在整个公交线路上协同运行。由于我们的问题是一个离散时间问题，两个相邻班次之间的发车间隔只能是时长 的整数倍。本文中将公交线路定义为有向图 G={S, L}，其中 S是沿公交线路的站点集合。

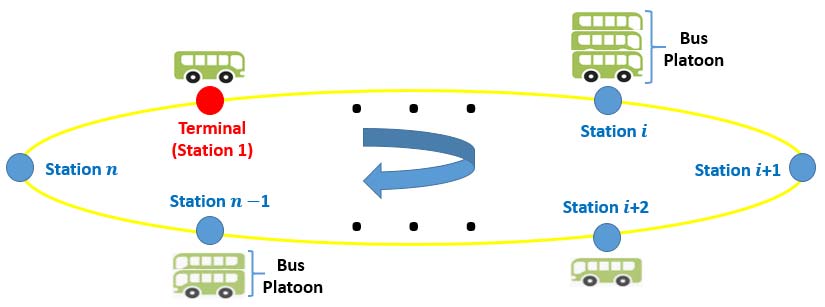
表I 符号与定义

符号	定义
S	沿公交线路的站点集合
L	两相邻车站之间的路段
B	公交车集合

为了便于技术开发，我们做出了一些假设，如下所示:

为了保证准点时刻表，每辆公交车在每个车站的停车时间为固定时长DTi。如果上车时间小于DTi，则公交车将在车站等待，直到固定时长DTi结束；否则，当上车时间达到DTi时，公交车将直接离开车站。此外，DTi足够长，以确保当公交车下车量满载时能够完成下车，即 α2 Capb ≤ DTi，其中 α2为每位乘客的平均下车时间， Capb为公交车b的容量。

本文未考虑车站之间的途中交通不确定性，且由于忽略了途中交通不确定性以及各车站公交车停车时间固定，因此本文也不考虑公交车超车现象。

第一个假设的加入旨在使重新调度操作易于实施，该假设将在我们的未来工作中予以放宽。为了更好地描述公交调度模型，表I总结了优化模型中使用的参数和决策变量。

A. 各站点客流量动态

车站i到目的站点j的客流量Pi , j(k)由流入量和上车流量决定，如下所述:
$$
Pi,j(k+ 1)= Pi,j(k)+ fi,j(k) −∑_{b∈B} Bb,i,j(k) \quad (1)
$$
其中，车站i前往目的站点j的乘客数通过到达乘客数fi,j(k)减去所有前往站点j的公交车上车乘客数∑Bb,i,j(k)的总和进行更新。

B. 每辆公交车内的客流量动态

每辆公交车内的客流量动态根据公交站进行更新，可以表示如下:
$$
∑ {j ∈S} Vb,i+1,j(k)=∑ {j ∈S} Vb,i,j(k)+∑_{j ∈S} Bb,i,j(k) − Ab,i(k)\quad (2)
$$
其中，公交车b在第k班次到达车站i+ 1时的乘客数量由其到达相邻上游站点i时的乘客数量、在车站i的上车流量 ∑Bb,i,j(k)以及在车站i的下车流量Ab,i(k)决定。

C. 上车客流约束

上车流量受相关的候车需求和目标上车公交车的剩余空间限制，可具体表示为如下:
$$
∑ {j ∈S} Bb,i,j(k) ≤ Capb −∑ {j ∈S} Vb,i,j(k) \quad (3a)
$$
$$
∑_{b∈B} Bb,i,j(k) ≤ Pi,j(k) \quad (3b)
$$
公式(3a)表明，上车乘客数不能超过公交车b的剩余空间。同时，公式(3b)描述了在车站i前往目的站点j的上车乘客总数不能超过在车站i前往目的站点j的候车乘客数。上述不等式对上车流量进行了限制，这使得上车流量成为另一组决策变量，即在我们的策略中实施了上车控制，以进一步优化多公交调度策略。

D. 下车流量约束

因此，班次k中公交车b在车站j的下车乘客数A不能超过以车站j为目的站点、在公交车b上的乘客数量，可描述如下:
$$
Ab, j(k) ≤∑_{q ∈S} Vb, q , j(k) \quad (4)
$$
其中∑Vb,q , j(k)表示在班次k中，从所有上游公交站上车、目的站点为j的公交车b上的乘客总数。

E. 公交车调度约束

上述上车流量Bb,i,j(k)、下车流量Ab,i(k)以及公交车载客量Vb,i,j(k)均与公交车调度分配xb(k)相关，即只有当公交车b在班次k被调度时，上述变量才在模型中对班次k起作用，可描述如下:
$$
(∀b ∈ B)(∀i,j ∈S) xb(k)= 0 ⇒ Bb,i,j(k)= 0 \quad (5a)
$$
$$
xb(k)= 0 ⇒ Ab,i(k)= 0 \quad (5b)
$$
$$
xb(k)= 0 ⇒ Vb,i,j(k)= 0 \quad (5c)
$$
公式(5a)表明，只有当公交车b被调度时，上车流量Bb,i,j(k)才可能非零。类似地，如果在班次k中公交车b未被调度，则下车流量Ab,i(k)和公交车载客量Vb,i,j(k)必须为0，如公式(5b)和(5c)所示。

F. 公交车停站时间约束

停站时间定义为公交车在车站停留且不移动的时间[36]。此外，公交装载时间是指允许乘客下车和上车所需的时间。停站时间在公共交通运营中起着重要作用。莱文森汇总了1957年至1980年间对美国多个城市公共交通停站时间的调查，发现停站时间约占城市地区总行驶时间的20%，而在中央商务区则增加至约26%[21]。此外，蒂拉奇尼发现，在采用车上支付票款的情况下，停站时间约占总行驶时间的15%[32]。

通常，描述载客时间的模型有两种：顺序模型和同时加载模型，这两种模型是根据上车流量和下车流量是否同时发生而建立的[31]。本文采用来自《公路通行能力手册》的一种同时加载模型[22]：
$$
L T= max(α1B, α2A)+ toc \quad (6)
$$
其中，LT表示公交车在车站的装载时间（单位：秒）， B 为在该车站的上车乘客数，A 为在该车站的下车乘客数， α1和 α2分别为每位乘客的平均上车时间和平均下车时间，具体取决于实际情况。toc为车门开关时间。

根据上述关系，现在我们可以建立第k班次公交车b在车站i的公交装载时间LTb,i(k)，如下所示:
$$
L Tb,i(k)= max(α1∑_j Bb,i,j(k), α2Ab,i(k))+ toc \quad (7)
$$
由于每辆公交车在每个车站等待时都设置了固定的停靠时间，因此我们也有:
$$
L T b,i( k) ≤ DT i \quad (8)
$$
因此，当车站i有大量等待乘客时，必须严格控制上车乘客总数，以满足约束(8)。

G. 公交车重新调度间隔

公交车在返回终点站后可以进行重新调度。由于本文未考虑道路不确定性，因此假设所有公交车完成一次无停靠的往返行程所花费的时间相同。除了非停靠往返时间Tr外，还应考虑公交车在每个车站的停车时间DTi，以形成公交重新调度模式中的完整的往返行程时间，相应地，公交调度约束描述如下:
$$
(∀b ∈ B, k ∈ R, k′ ∈ N+)
xb(k)= 1 ⇒
\left\lfloor \frac{Tr+∑i DTi}{\Delta}\right\rfloor
∑_{k′=1}
xb(k+ k′)= 0 \quad (9)
$$
这表明公交车b在完成环行班次之前无法被重新调度。Ns是公交线路沿线的站点数量，而 ⌊·⌋是不大于输入参数的最大整数。

H. 环路整体目标成本

我们的目标函数中包含了三个不同的性能指标：乘客总等待时间、乘客感知等待时间和公交车总空置。

1) 乘客总等待时间：

通过将最小发车间隔 Δ 与候车乘客数量相乘，可得到所有车站和计划班次的乘客总等待时间估计值，该值由以下公式表示:
$$
Jtd= ∑ {i,j ∈S} ∑ {k=1}^N Pi,j(k)Δ \quad (10)
$$
其中N为预测步长，预测时域Hp= NΔ。

2) 乘客感知等待时间：

在成本函数中，通常最小化的是实际的乘客延误或等待时间，而非乘客的心理感知。然而，对等待时间的感知会显著影响乘客的交通方式选择[11],[35]，且运输服务质量通常由乘客感知延误[24],[29]来评估。此外，最小化线性等待时间忽略了那些等待时间特别长的乘客，而通过最小化乘客感知延误可以弥补这一缺陷。通过将乘客焦虑纳入我们的目标函数，我们能够捕捉个体效益，从而实现用户均衡。相应的乘客感知等待时间建模如下。

我们假设乘客在班次k+ 1和班次k与k+ 1之间到达时，其预期上车时间为该时段内的班次，若他们无法在预期班次k+1上车，则会产生不满。

这种不满（在本文中以感知等待时间来衡量）由以下非线性函数捕捉:
$$
D(i,j, k+ 1, m)
= max\left{fi,j(k) − max\left[∑ {b∈B} ∑ {l=k+1}^m Bb,i,j(l)
−(Pi,j(k) −∑ {b∈B} Bb,i,j(k)), 0\right], 0\right}θ(m −(k+ 1))\quad (11)
$$
公式(11)描述了一组以站点j为目的站点的乘客的感知时间，这些乘客在第k次行程与第k+ 1次行程之间到达站点i，并且直到第m次行程仍未登上公交车。∑Bb,i,j(l)表示从第k+ 1次行程到第m次行程期间，在站点i以目的地站点j为目标的公交车b的上车流量之和，记为l=k+1，该流量可分为两部分：在第k+ 1次行程之前到达的上车流量和在第k+ 1次行程之后到达的上车流量。 ∑ {b∈B} ∑ {l=k+1}^m Bb,i,j(l)表示从第k+ 1次行程到第m次行程期间，在站点i以目的地站点j为目标的所有上车流量。Pi,j(k) − ∑ {b∈B} Bb,i,j(k)表示第k次行程的公交车刚离站后仍滞留在站点的剩余乘客数，这些乘客全部是在第k次行程之前到达的。项max[∑ {b∈B} ∑ {l=k+1}^m Bb,i,j(l)−(Pi,j(k)−∑ {b∈B} Bb,i,j(k))， 0]表示在第k次行程之后到达站点i、以目的地站点j为目标并在第k+ 1至第m次行程之间上车的乘客数量，因为在该项中，第k次行程之前到达的乘客（即Pi,j(k)−∑ {b∈B} Bb,i,j(k)）已被扣除。此外，项max{fi,j(k)−max[∑ {b∈B} ∑ {l=k+1}^m Bb,i,j(l)−(Pi,j(k)−∑_{b∈B} Bb,i,j(k))， 0], 0}刻画了以目的地站点j为目标、在第k次行程与第k+ 1次行程之间到达但到第m次行程后仍在站点i等待的乘客数量。项θ(m−(k+1))是其自变量的非线性函数，例如指数函数，而 θ(m−(k+1))表示从预期到达的第k+ 1次行程起已流逝的感知时间。

根据上述描述，所有站点在整个规划周期内乘客感知的总等待时间为如下:
$$
Jpd= ∑ {i,j ∈S} ∑ {k=1}^{N−1} ∑_{m=k+1}^N D(i,j, k+ 1, m) \quad (12)
$$

3) 公交车总空置：

我们还试图从公交运营商的角度最小化每辆公交车的空座位，以提高公交车利用率，具体表示如下:
$$
Jbv=∑ {b∈B} ∑ {k=1}^N ∑ {i∈S} (Capb −∑ {j ∈S} Vb,i,j(k)) \quad (13)
$$

4) 多公交车调度模型的最优目标函数：

我们考虑两种不同的目标，第一种是线性成本 JCost 1，第二种是非线性成本 JCost 2。

线性成本旨在最小化乘客总等待时间和公交车总空置，其表达式如下:
$$
minJCost 1 = min Ctd Jtd+ Cbv Jbv \quad (14)
$$
其中Ctd和Cbv分别为乘客总等待时间和公交车空位的权重系数。上述方程为线性函数，可通过混合整数线性规划求解器和进化算法（EA）求解。

然而，由于乘客感知等待时间中涉及的非线性因素，第二个目标JCost2无法通过混合整数线性规划求解器高效求解，如下所示:
$$
minJCost2= min Cpd Jpd+ Cbv Jbv \quad (15)
$$
其中Cpd是乘客感知等待时间的权重系数。

文献中已讨论了乘客延误与公交车载客率之间的双目标分析[18]。本模型的成本旨在通过加权和法，在一个整体的单目标函数中研究乘客延误和公交车载客率的货币成本。公交车的空座位可转换为相应的载客率或负载系数，进而转化为公交车利用率以及运营成本。上述权重系数可定义为经济考量中的货币价值。此外，这些权重的取值也可被确定，以反映需求方和运营商方的优先级水平。

基于上车控制的多公交调度策略

III. 求解算法

多公交车调度与上下车管理（MBDBM）问题已被建模为混合逻辑动态模型，该模型包含线性成本函数(14)或非线性成本函数(15)，以及混合逻辑约束，例如公交车调度约束(5)、公交车重新调度约束(9)，和线性约束，例如站点流量动态(1)、公交车载客量动态(2)、上车客流约束(3)和下车流量约束(4)。在本节中，首先针对线性成本函数建立混合整数线性规划模型，然后讨论使用遗传算法（GA）和和声搜索算法（HS）来求解线性和非线性两种情况下的问题。

A. 公交车调度模型的混合整数线性规划模型

第二节中描述的逻辑约束包括公交车调度约束(5)、公交车停站时间约束(7)和(8)，以及公交车重新调度约束(9)。令M1选择得足够大，例如M1 ≥maxk(Bb,i,j(k),Ab,i(k), Vb,i,j(k))，那么约束条件(5)可转化为以下形式:
$$
Bb,i,j(k) ≤ M1xb(k) \quad (16a)
$$
$$
Ab,i(k) ≤ M1xb(k) \quad (16b)
$$
$$
Vb,i,j(k) ≤ M1xb(k) \quad (16c)
$$
命题1 ：在模型中用不等式（16）替换约束条件（5）会得到相同的解。

通过整合约束(7)和(8)，公交车停站时间约束可重写为以下不等式：
$$
max(α1∑_j Bb,i,j(k), α2Ab,i(k))+ toc ≤ DT_i \quad (17)
$$
上述约束条件可以转化为以下线性约束条件:
$$
α1∑_j Bb,i,j(k) ≤ DT_i − toc \quad (18a)
$$
$$
α2Ab,i(k) ≤ DT_i − toc \quad (18b)
$$
命题2 ：在模型中用不等式(18)替换约束(7)和(8)会得到相同的解。

同样，令M3选择得足够大，例如M3 ≥⌊(Tr+∑iDTi)/Δ⌋ × maxk(∑ xb(k+k′))，那么约束(9)可以转化为以下形式:
$$
⌊(Tr+∑i DTi)/Δ⌋ ∑_{k′=1} xb(k+ k′) ≤ M3(1 −xb(k)) \quad (19)
$$
命题3 ：在模型中用不等式(19)替换约束(9)会得到相同的解。

最后，我们可以将MBDBM问题转化为如下的混合整数线性规划问题:
- 最小化 (14)
- 满足以下约束条件 ：
- C1：站点客流量动态(1)
- C2：公交车载客量动态(2)
- C3：上车客流约束(3)
- C4：下车客流约束(4)
- C5：公交发车调度约束(16)
- C6：公交停站时间约束(18)
- C7：公交重新调度约束(19)

B. 求解MBDBM的进化算法

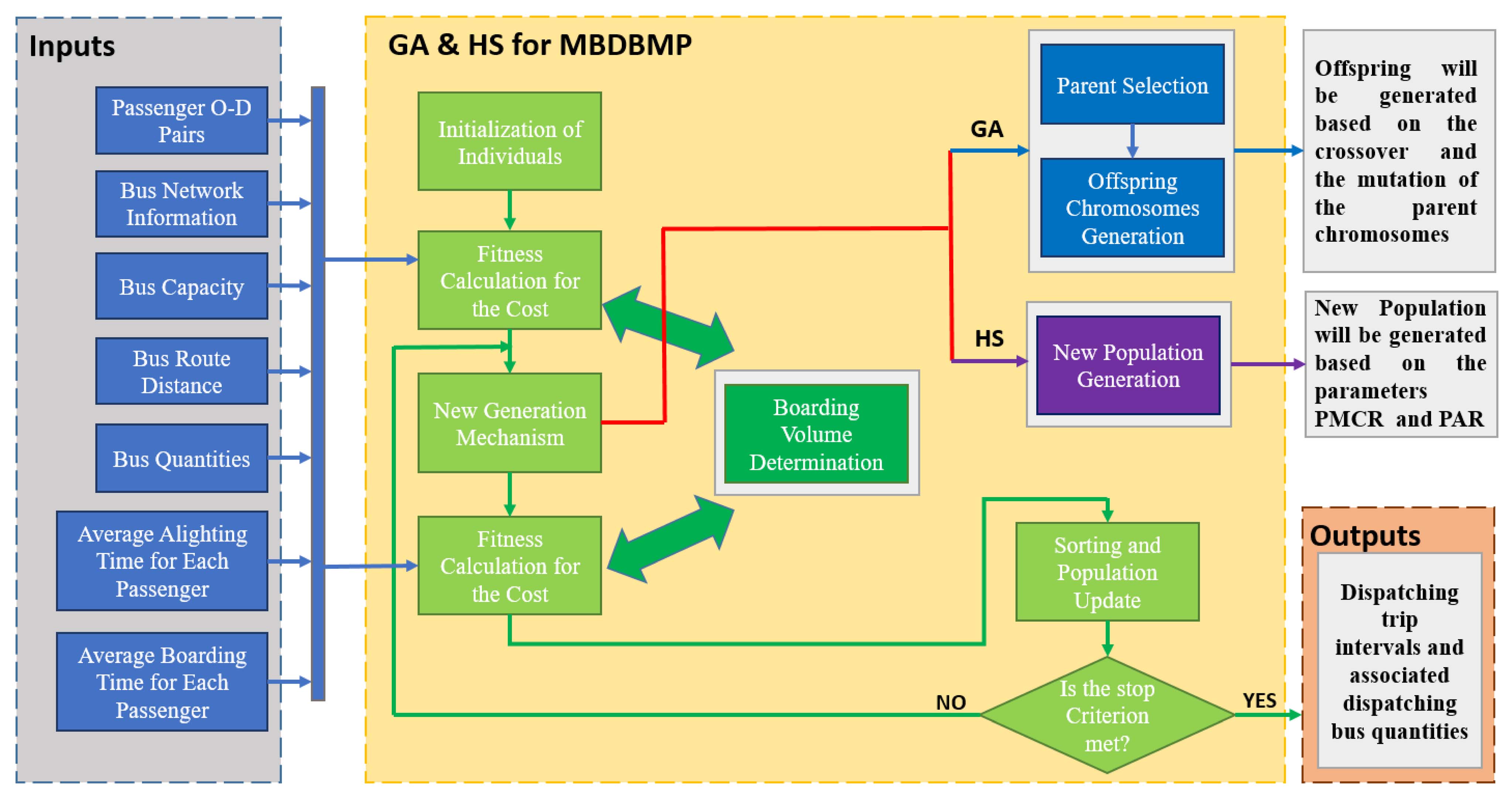
请注意，我们提出的模型是一个NP难问题，具有非线性目标，并涉及大量逻辑约束。因此，在将目标函数线性化并将逻辑约束转换为相应的线性约束后，使用基于梯度的数学方法或分支定界算法求解该问题将耗费大量时间。鉴于此，采用两种典型的进化算法——遗传算法(GA)和和声搜索(HS)算法来求解我们的问题。GA和HS均已成功应用于许多城市交通调度问题，均获得了高质量的解和合理的计算时间[5],[38],[40]。本文采用带有精英父代选择和单点交叉的遗传算法，整个GA和HS的具体流程如图2所示。

首先，在初始化步骤中，决策变量xb(k)的种群被随机生成，每个个体在遗传算法和和声搜索算法中分别称为染色体和和声。然后，生成的调度指标结合图2输入模块提供的初始信息，传入适应度函数。之后，基于前一代种群生成新种群：在遗传算法中，选择性能较好的父代染色体，通过交叉方法或变异方法在下一步生成子代。在通过适应度函数对后代进行评估后，性能较好的染色体将在下一代循环中保留，而具有较差成本值的染色体则从种群中移除。而对于和声搜索算法，新的“和声”由两个重要参数决定：和声记忆考虑率（HMCR）和音调调节率（PAR）。HMCR表示从现有个体中选择数值的概率，PAR表示对现有个体进行微调的概率。新的“和声”可以通过三种不同方式获得：直接使用现有种群中的个体、对现有个体进行轻微修改或基于上下界重新初始化。整个过程如算法1所示，其中算法1中的变量Xi表示种群中的第ith个解，它是一个n维向量Xi={Xi(1), Xi(2), ···, Xi(k), ···, Xi(n)}，包含优化问题的 n个决策变量，LB(k)和UB(k)分别是决策变量Xi(k)的下界和上界。此外，rand()、rand1() 和 rand2() 均表示在0和1之间随机生成数值。BW为带宽，用于寻找可能的邻域解。接下来，计算新生成种群的适应度。通过与前一代种群产生的结果比较，在图2的排序与种群更新模块中保留相对较低成本的个体，以形成新的种群。上述过程持续进行，直到满足停止准则。最终，在预设迭代次数后获得最优发车间隔。

算法1 生成新和声向量

If(rand1() < HMCR)
    Xnew(k) = Xi(k) 
    If(rand2() < PAR) 
        Xnew(k) = Xnew(k) ± rand() × BW 
    End
Else 
    Xnew(k) = LB(k) + (UB(k) − LB(k)) × rand() 
End

二进制变量、公交车调度指示符xb(k)的初始化在算法 2中进行描述。在步骤1中，调度指示符xb(k)被随机初始化，使用函数rand()随机生成整数0或1。为了满足最小往返时间的要求，添加了步骤1.2以保证虚拟公交重调度模式：对于当前班次k′之前的任意班次k，如果公交车b在班次k′被调度，且班次k′与班次k之间的时间间隔小于规定的返回时域T(T= Tr+∑i DTi)，则公交车不能在班次k被调度。

除了上述在初始模块或新生成模块中确定的决策变量（如图2所示的二进制变量xb(k)）之外，我们还有一些整数型决策变量。这是由于不等式(3)、(4)和(17)的存在，导致整数变量 Bb,i,j(k)和 Ab,i(k)也成为了决策变量。

方程(2)中描述的公交车流量动态可以重写如下，只要车站j在车站i+ 1之后，就不需考虑下车流量Ab,i(k)。
$$
Vb,i+1,j(k)= Vb,i,j(k)+ Bb,i,j(k) \quad (23)
$$
在对公交车流量动态进行这种简化后，我们只需考虑上车流量变量 Bb,i,j(k) 的初始化。在约束条件(3b)中，j 是 Vb,i,j(k) 所对应的站点，即站点 i 之后的站点，亦即 j > i；而在成本函数(14)和(15)中的 j 对于 Vb,i,j(k) 则表示站点 i−1 之后的所有站点，亦即 j ≥i。

我们假设每个车站的停站时间DTi不小于公交车满载下车乘客时的下车时间，即 α2Capb ≤ DTi，这表明在任何站点的任何下车过程中，下车时间不超过停站时间DTi，换句话说， α2Ab,i(k) ≤DTi。因此，约束条件(17)可转化为以下不等式，且无需考虑下车流量:
$$
α1∑_j Bb,i,j(k)+ toc ≤ DTi \quad (24)
$$
上述不等式可重写如下:
$$
∑_j Bb,i,j(k) ≤⌊(DTi − toc)/α1⌋ \quad (25)
$$
最后，我们只需关注上车流量的分配，以满足约束条件(3)、(4)和(25)。

上车流量变量 Bb,i,j(k)在适应度计算阶段确定，如图 2所示。同时，它根据每个车站停靠的公交车数量（算法 2的结果），由一个随机实数分数 η 进行解码。以下方程描述了班次 k 的 N 辆公交车（b1, b2,…, bm,…, bN）在车站 i 停靠的情况：
$$
B^{demand} {b1,i,j}(k)= ⌊Pi,j(k)η1⌋ \quad (26a)
$$
$$
B^{demand} {bm,i,j}(k)= ⌊Pi,j(k) \prod_{p=1}^{m−1} (1 − η_p)η_m⌋ \quad (26b)
$$
$$
B^{demand} {bN,i,j}(k)= ⌊Pi,j(k) \prod {p=1}^{N−1} (1 − η_p)⌋ \quad (26c)
$$
其中η1,…, ηm,…, ηN−1均为随机生成的0到1之间的实数值，且 ⌊·⌋为不大于输入参数的最大整数。

在车站i处等待的乘客可能的目的站点数量列为i+1,i+2,…,Ns,1（若i不是终点站（i> 1）），或i+1,i+2,…,Ns（若i为第一站），其中 Ns表示环线路线上总的站点数量。我们使用g1, g2,…, gm,…, gN表示车站i的可能目的站点。相应地，由公交车空位决定的公交车b的上车流量如下所示:
$$
B^{bus} {b,i,g1}(k)= ⌊(Cb −∑_j Vb,i,j(k))η1′⌋ \quad (27a)
$$
$$
B^{bus} {b,i,gm}(k)= ⌊(Cb −∑ j Vb,i,j(k)) \prod {p=1}^{m−1}(1 − η′ p)η′_m⌋ \quad (27b)
$$
$$
B^{bus} {b,i,gN}(k)= ⌊(Cb −∑ j Vb,i,j(k)) \prod {p=1}^{N−1}(1 − η′_p)⌋ \quad (27c)
$$
其中η′1,…, η′m,…, η′N−1是随机生成的介于0和1之间的实数值。

类似地，由推导出的停站时间约束所确定的上车流量可表示如下:
$$
B^{time} {b,i,g1}(k)= ⌊(DTi − toc)/α1 η′′1⌋ \quad (28a)
$$
$$
B^{time} {b,i,gm}(k)= ⌊(DTi − toc)/α1 \prod_{p=1}^{m−1}(1 − η′′ p)η′′_m⌋ \quad (28b)
$$
$$
B^{time} {b,i,gN}(k)= ⌊(DTi − toc)/α1 \prod_{p=1}^{N−1}(1 − η′′_p)⌋ \quad (28c)
$$
其中η′′1,…, η′′m,…, η′′N−1也是随机生成的0到1之间的实数值。

公交车bm在目的站点gm的最终上车乘客数为上述方程的最小值，可表示如下:
$$
B_{bm,i,gm}(k)= min(B^{demand} {bm,i,gm}(k), B^{bus} {bm,i,gm}(k), B^{time}_{bm,i,gm}(k)) \quad (29)
$$
上车限制策略已在许多以往的研究中被采用，其优势也已得到说明[7],[8],[41]。然而，大多数策略仅针对公交运营设计，而非公交调度，这与本研究存在显著差异。

从实施角度来看，智能交通系统中近年来信息与通信技术（ICT）的进步[10],[23]为控制上车流量提供了可能的途径。该方式可通过到站公交车与候车乘客之间的通信实现。到达的公交车将通过移动应用程序或车站屏幕向站台前方队列中的相关乘客发送消息，通知其进入指定的上车区域。当公交车抵达车站时，仅允许在指定区域内等待的乘客上车。因此，可能还需对公交站台进行基础设施升级，以划分候车区域和上车区域。通过这种方式，公交运营商可有效控制车队中每辆公交车的上车乘客数，并为下游车站的乘客保留必要的载客空间，避免公交车在上游站点就已满载，导致后续站点乘客无法上车的情况发生。

表II 案例研究中使用的参数

参数	值
公交车容量 Capb	100
平均上车时间 α1	3秒/人
平均下车时间 α2	2秒/人
车门开关时间 toc	5秒
固定停靠时间 DTi	30秒
非停靠往返时间 Tr	60分钟
预测时域 Hp	120分钟

表III 案例1至案例8的初始设置

案例	Nb	Ns	Nx	Ncons
1	3	10	300	4371
2	3	15	450	6556
3	3	20	600	8741
4	3	25	750	10926
5	5	10	500	7285
6	5	15	750	10926
7	5	20	1000	14567
8	5	25	1250	18208

IV. 数值示例

为了保证实时控制，所提算法的计算效率是必需的。因此，我们首先在不同公交站点数量和预测时域下测试该方法，以观察最终调度策略能够多快得到。之后，将所提模型应用于一条设有10个均匀分布公交站点的环线路公交线路。通常，一辆大型单层公交车可容纳60至120名乘客（包括站立乘客）[27]。在我们的仿真中，假设每辆公交车的容量为100名乘客，每条公交线路由5辆公交车运营。各站点的起讫点对通过调用C语言中的rand()函数随机生成++，生成的起讫点对是在指定种子下的伪随机数。所提策略首先在第IV-B节与传统方法进行比较，然后进一步讨论不同目标的影响。案例研究中使用的参数列于表II中。

计算复杂度

将所提的MBNBM问题转化为混合整数线性规划问题后，首先使用商业求解器Gurobi[15]求解具有线性成本的MBNBM问题。然后采用遗传算法和和声搜索算法实时求解该问题。程序代码在配备英特尔酷睿i7-4770处理器 @3.40GHz和8GB内存的PC上运行。由于本小节旨在检验所提算法的计算效率，因此各项成本对应的具体权重均设为1，不考虑彼此之间的相互影响。遗传算法的变异概率和交叉概率均设为0.5[39]。和声搜索算法的参数HMCR和 PAR分别设为0.95和0.5[14]。为保证比较的公平性，每种情形均进行15次实验，种群大小为50，每次实验的迭代次数为1000。

表III给出了案例1到案例8的初始设置，其中Nb和 Ns分别表示公交车数量和站点数量，Nx和Ncons 分别表示相关案例的决策变量和约束条件的数量。表IV和表V分别描述了在线性成本下，从案例1到案例8的MILP&GA和MILP&HS的计算时间及性能成本。此外，表VI展示了在非线性成本下，从案例1 到案例8的GA&HS的计算时间和性能成本。GA和HS在乘客等待时间、公交车空位以及计算时间方面的15次实验平均结果已在表IV、表V和表VI中报告。

显然，计算时间随着问题规模的增加而逐渐增加。对于一条由3辆公交车运营、包含10个车站、预测时域为10步、返回时域为6步的公交线路，计算仅耗时3.0359秒，相当于求解一个包含3144个整数和二进制决策变量以及4371个约束条件的混合整数线性规划问题，且计算耗时仅占总时间的0.51%（3.0359秒/10分钟），这显然保证了实时调度。另一方面，遗传算法（GA）和和声搜索算法（HS）所需的计算时间较长，分别为46.7609秒和46.5035秒。然而，随着问题规模的增加，混合整数线性规划（MILP）的计算时间呈指数级增长，其实时调度的概率也随之降低。在案例8中，对于一条包含25个公交站点、预测时域为120分钟的公交线路，最终耗时3410.3秒，超过发车间隔的5倍，这显然无法保证实时公交调度操作的实现。与此同时，进化算法的优势变得越来越明显。在案例8中，遗传算法（GA）和和声搜索算法（HS）分别仅需320.8330秒和311.772秒即可完成1000次更新。此外，混合整数线性规划（MILP）得到的实际性能结果J∗cost1以及遗传算法（GA）和和声搜索算法（HS）的计算结果Jcost1均列于表IV和表V中。差距度 (Jcost1 − J∗cost1)/J∗cost1用于说明数学优化算法与进化算法之间的差异。显然，该差距非常小，低于所有8种情况均为15%。然而，GA和HS的计算时间显著下降，尤其是大规模案例。这表明采用GA或HS可以在确保适当退化范围的同时保证快速计算。

表VI展示了非线性成本下的计算时间和结果性能。与表IV和表V类似，HS的计算时间略小于GA，这可能是由于GA中额外增加了父代选择阶段。此外，当问题规模较小时，HS的表现优于GA。然而，随着问题规模的增大，GA最终优于HS，这表明HS在小规模案例中具有良好的探索能力，而GA在大规模案例中具有较好的开发能力。这两种算法的特性可能源于其不同的更新机制：新和声可以根据变量的上下界重新初始化，而新染色体只能从选定的父代即现有种群中继承。然而，GA与HS之间并无显著差异。一个可能的原因是，如第三节-B所述，本问题还需要在适应度计算过程中确定整数变量，这是由于上车控制所导致的。如公式(26)、(27)和(28)所示，分配给上车人数的随机生成值可被视为施加在确定的调度指标xb(k)上的噪声。由于这些变量在适应度阶段才被确定，而非在新种群生成阶段，因此其具有良好特性的实例无法传递到下一次迭代，同时其随机性可能会降低算法的更新效率，从而导致两种算法之间的差异较小。此外，由于篇幅限制，关于参数设置以及进化算法收敛速度影响的详细讨论将在我们的未来工作中进行。

此外，表VI中的成本Jtd略大于表IV和表V中的对应值，因为非线性成本的目标函数是Jpd和Jbv的总和。尽管优化非线性成本导致了更大的线性等待时间Jtd，但它为等待时间更长的乘客提供了更多益处。通过最小化非线性成本，我们从一个新的角度刻画了乘客的焦虑情绪，从而在用户均衡（个体等待时间）与系统最优（总等待时间）之间实现了权衡。

B. 我们的方法与传统调度策略之间的成本比较

为了展示我们多公交调度策略的优势，我们将该策略与传统固定调度策略和优化的单公交策略进行了比较。固定调度策略要求每个班次仅dispatch一辆单辆公交车，且公交车发车顺序和发车间隔均固定不变。优化的单公交策略同样为每个班次dispatch一辆公交车，但可根据相同的成本对公交车发车顺序和发车间隔进行优化。

我们提出的方法。考虑一条包含10个公交站和终点站内5辆公交车的公交线路。预测时域为120分钟，往返时间为60分钟。在客流量从20400至30000、以每2400名乘客为间隔递增的情况下，对由方程(14)和(15)描述的两种不同成本均进行了测试。

图3展示了在优化线性成本Jcost1时，所提策略与其他两种策略在不同客流量输入下的性能表现。具体而言，图3a、图3b和图3c分别描绘了总成本Jcost1、乘客实际延误Jtd和公交车空位Jbv。其中，蓝线、红线和绿线分别对应所提策略、单公交优化策略和固定策略。如图3a所示，三种策略的总成本以及图3b中乘客的线性等待时间均随着乘客incoming客流量的增加而逐渐增大。显然，我们的方法在总成本和乘客实际延误两个方面均优于其他两种策略。尽管另外两种策略在上述两项性能上不如所提策略，但它们在图3c中的公交车空位却大幅降低，尤其是单公交优化调度策略。由于这两种策略未实施上车控制，即上车流量仅由需求和公交车空位决定，因此当车内有足够剩余空间时，车站内的所有候车乘客都将上车。然而，在我们的策略中，上车流量是决策变量，只有部分等待乘客能够成功上车，公交车即使仍有容纳乘客的空间也会直接离开当前车站驶向下一站点。这是因为我们希望为后续站点的乘客保留必要的空间，以避免其长时间等待，但这也会导致图3c中较高的公交车空位结果。然而，随着乘客数量的增加，固定策略在高公交车利用率方面的优势变得不那么明显，因为所提策略的公交车空位随乘客数量增加而显著减少，导致所提方法与固定方法之间的差距越来越小。另一方面，单公交调度方法的公交车空位仍随着乘客需求的增加而急剧下降。

类似地，图4展示了在优化非线性成本Jcost2时，所提策略、单公交优化策略和固定策略在不同乘客数量输入下的性能表现。其中，图4a、图4b和图4c分别描绘了总成本Jcost2、乘客感知延误Jpd以及相应的公交车空位Jbv。蓝线、红线和绿线分别代表所提策略、单公交优化策略和固定策略的结果。随着乘客数量的增加，图4a中的总成本和图4b中的乘客感知等待时间在两种策略下均相应增加。同时，随着乘客数量的增加，本方法与另外两种方法在总成本和乘客感知等待时间上的差距也越来越大。然而，与另外两种方法相比，本方法的公交车利用率较低。此外，不同于图3c中绘制的公交车空位图，本方法与另外两种方法之间的变化不大。原因将在第四节-C中详细说明。尽管我们提出的方法导致较高的公交车空位，但在减少乘客等待时间方面带来了更多优势。通过比较图3b和图4b，可以发现当应用非线性成本时，单公交优化策略的效果减弱，因为它之前在图3b中接近蓝线，而现在在图4b中接近绿线。这表明上车控制在防止乘客感知等待时间呈指数增长方面发挥了重要作用。

为进一步说明我们方法的优势，下文将讨论所提策略与固定策略之间的性能差异。图5和图6分别描绘了实施所提出的方法后线性成本和非线性成本的性能差异，其中图5（图6）中的蓝色条形Rtd(Rpd)、红色条形Rbv以及黄色条形Rcost1(Rcost2)分别表示乘客等待时间、公交车空位和总成本的差异程度，其定义将在下文详细解释。

$$
Rtd= \frac{J^{propose} {td} − J^{fix} {td}}{J^{fix} {td}} \quad (30a)
$$
$$
Rbv= \frac{J^{propose} {bv} − J^{fix} {bv}}{J^{fix} {bv}} \quad (30b)
$$
$$
Rcost1= \frac{J^{propose} {cost1} − J^{fix} {cost1}}{J^{fix} {cost1}} \quad (30c)
$$
其中，公式(30a)对应于优化线性成本(14)时的图5。J^{propose} {td}和J^{fix} {td}分别为所提策略和固定策略下的乘客实际等待时间。同样，J^{propose} {bv}和J^{fix} {bv}分别为所提策略和固定策略下的公交车空位值。类似地，J^{propose} {cost1}和J^{fix}_{cost1}分别为所提策略和固定策略下的总成本值。

$$
Rpd= \frac{J^{propose} {pd} − J^{fix} {pd}}{J^{fix} {pd}} \quad (31a)
$$
$$
Rbv= \frac{J^{propose} {bv} − J^{fix} {bv}}{J^{fix} {bv}} \quad (31b)
$$
$$
Rcost2= \frac{J^{propose} {cost2} − J^{fix} {cost2}}{J^{fix} {cost2}} \quad (31c)
$$
其中，公式(31)对应于当非线性成本(15)被优化时的图6。J^{propose} {pd}和J^{fix} {pd}分别为所提策略和固定策略下的乘客感知等待时间。同样，J^{propose} {bv}和J^{fix} {bv}分别为所提策略和固定策略下的公交车空位。类似地，J^{propose} {cost2}和J^{fix}_{cost2}分别为所提策略和固定策略下的总成本。

显然，在所有情况下，乘客等待时间和总成本的减少都非常显著，这在图5和图6中分别由蓝色条形和黄色条形体现出来。然而，公交车空位的增加（即两幅图中的红色条形）在所有情况下都非常小。这表明，略微牺牲公交车空位便能同时降低总成本和乘客等待时间，生动地说明了我们策略的有效性。值得注意的是，随着乘客数量的增加，图5中的蓝色条形逐渐变小，但这一现象在图6中并未出现。这是因为随着乘客数量的增加，乘客线性等待时间J^{propose} {td} −J^{fix} {td}的差距相当稳定，从而导致当分母J^{fix}_{td}增大时，比率Rtd随之减小。

C. 非线性乘客感知等待时间对公交车载客时间的影响

如第IV-B节所述，不同的成本函数在不同客流量下导致公交车空位不同，分别如图3c和图4c所示。为了清晰地说明不同目标的影响，绘制了图7以描述在三种不同的乘客情况下两个目标(14)和(15)的平均装载时间。

与第IV-B节类似，本文中的示例也考虑了一条包含10个公交站和终点站内5辆公交车的公交线路。预测时域为120分钟，往返时间为60分钟，总乘客量分别为12000、24000和36000。在相同的客流量输入下，随机生成了五个案例，其起讫点对各不相同。蓝色条形对应线性成本，红色条形对应非线性成本。此外，平均加载时间AvgLoad的具体定义如以下公式所示。
$$
AvgLoad= \frac{∑ {i∈S}∑ {b∈B} LT_{b,i}(k)}{Ns∑ {k=1}^{Hp}∑ {b∈B} xb(k)} \quad (32)
$$
平均装载时间随着总乘客数量的增加而增加，这可以通过图7a、图7b和图7c中y轴的范围反映出来。此外，非线性成本下的平均装载时间始终低于线性成本。在线性成本下，乘客等待时间呈线性增长，而在非线性成本下，乘客感知等待时间随时间呈指数增长。因此，采用非线性成本的策略将允许较少乘客上车，以预留更多空间接载后续站点的乘客，从而最小化呈指数增长的乘客不满。因此，上车控制导致图7中红色条形所示的较低装载时间，进而使得非线性目标相比线性目标具有更高的公交车空位。

V. 结论

本文针对简化的道路公交运输系统提出了一种多公交调度策略。允许从终点站发出单辆公交车或公交车队，从而实现可变公交规模以满足波动的乘客需求。通过控制每个车站的上车流量，为下游车站的乘客预留必要的载客容量。采用同步加载模型来描述公交上车过程，从而构建更为真实的模型。尽管当前模型尚未考虑途中交通不确定性，但将在基于当前框架的未来模型中引入该因素。同时，所提策略中使用非线性函数刻画乘客感知等待时间，以反映因等待时间延长而导致的乘客不满。为了兼顾需求方和供给侧的利益，目标函数中综合考虑了乘客感知等待时间、乘客实际等待时间和公交车空位。采用了典型的混合整数线性规划求解器（如Gurobi）以及进化算法（遗传算法GA和和声搜索算法HS）来求解该问题。仿真结果表明，GA和HS能显著减少计算时间，同时确保可接受程度的性能下降。此外，将所提方法与传统调度策略进行了比较，结果表明所提方法的性能优于其他策略。另外，两种不同目标的影响体现在公交车平均停靠时间上，表明考虑乘客感知等待时间有助于促进公交上车过程，并最小化后续站点乘客的等待时间。