在当今人工智能领域,多模态大语言模型(MLLMs)已成为研究热点,它们能够同时理解和处理文本、图像、音频等多种信息形式。然而,这些模型在面对新任务时需要不断微调,在此过程中会产生一个棘手的问题——灾难性遗忘。就像学生为了学习新知识而突然完全忘记旧知识一样,模型在适应新任务时,可能会严重损害其在原有任务上的表现。
本文将深入解读一篇名为《AdaDARE-γ: Balancing Stability and Plasticity in Multi-modal LLMs through Efficient Adaptation》的论文,该论文提出了一种创新方法,有效解决了这一难题。
多模态大模型适应中的核心挑战
灾难性遗忘:稳定与塑性的两难抉择
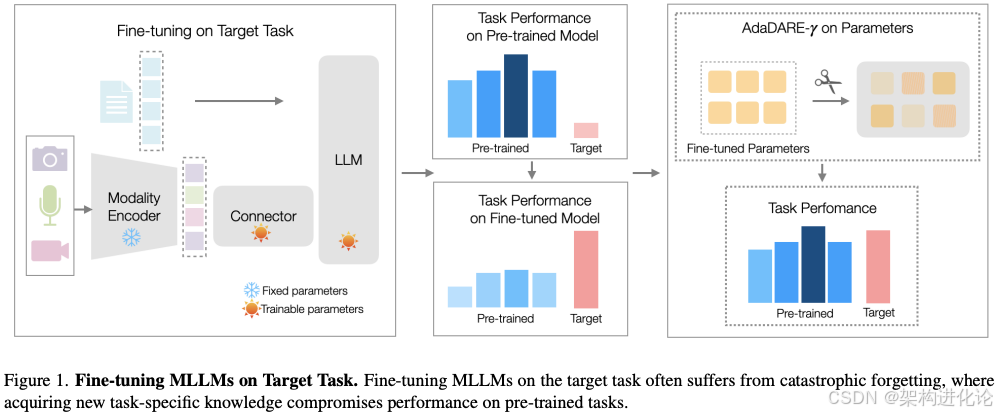
灾难性遗忘现象是持续学习领域的核心问题。当我们对预训练好的多模态大模型(如InstructBLIP和LLaVA-1.5)在新任务上进行微调时,模型参数会发生变化以适应新任务,但这个过程却会覆盖掉已经学到的原有知识。
这就引出了两个关键概念:稳定性(stability)指模型保持已获得知识的能力;塑性(plasticity)则指模型学习新知识的能力。在传统微调方法中,这两者往往存在权衡关系——提高塑性通常会损害稳定性,反之亦然。
例如,一个能够识别鸟类和描述风景的多模态模型,当我们需要它新增识别汽车品牌的能力时,直接微调可能导致它在鸟类识别或风景描述上的性能显著下降。这种情况在实际应用中是不可接受的。
现有解决方案的局限性
目前,解决灾难性遗忘的主要方法包括:
-
经验回放(Experience Replay):保存一部分旧数据与新数据一起训练。但这种方法面临存储开销和数据隐私问题。
-
正则化方法:对重要参数的变化添加约束,但通常会限制模型适应新任务的能力。
-
参数隔离:为每个任务分配独立的模型参数,但这会导致模型参数线性增长。
这些方法在平衡稳定性和塑性方面都存在明显不足。正如论文中提到的,传统的经验回放方法采用随机采样策略来选择要回放的记忆,这种策略效率低下。而其他方法往往无法在保留预训练知识的同时,高效地获取新任务能力。
AdaDARE-γ的技术创新
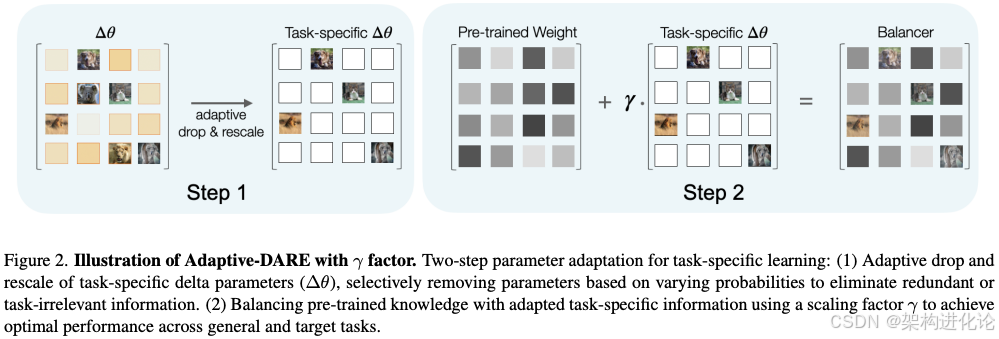
AdaDARE-γ方法的核心思想是精确控制参数更新,有选择性地融入新任务知识,而非盲目地覆盖所有参数。该方法通过两个关键技术实现了这一目标:自适应参数选择机制和受控任务特定信息注入策略。
自适应参数选择机制
AdaDARE-γ不是对模型中的所有参数进行同等程度的更新,而是智能识别那些对新任务最重要的参数。具体来说,它通过比较预训练模型和微调后模型的参数变化,选择变化最显著的那些参数作为候选更新参数。
这种选择的数学基础是:假设我们有预训练模型参数θ₀和微调后参数θ₁,我们计算参数变化量Δ = |θ₁ - θ₀|。然后,根据变化量的大小对参数进行排序,选择Top-K%变化最大的参数作为潜在更新候选。
下面的时序图展示了AdaDARE-γ的自适应参数选择过程:
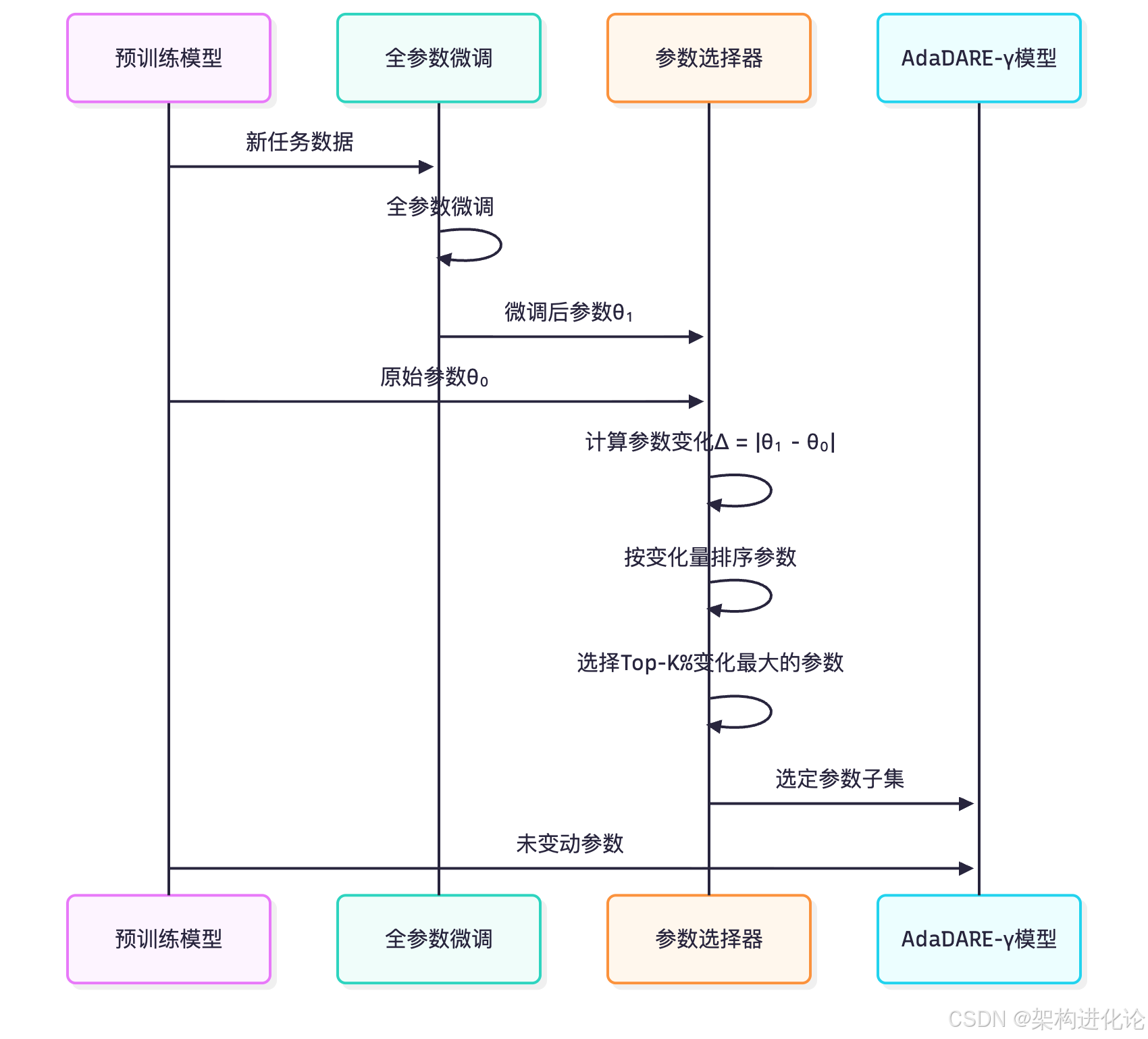
这种方法的关键洞察是:不同参数对新任务的敏感度不同,只有一部分参数对学习新任务至关重要,而其他参数可以保持相对稳定,从而保护已学到的知识。
受控任务特定信息注入策略
选定重要参数后,AdaDARE-γ并不是直接使用这些更新后的参数,而是采用一种受控的注入方式,将新任务知识融入预训练模型。具体而言,它通过加权组合预训练参数和微调参数来实现这一平衡:
θ_ada = θ₀ + γ · (θ₁ - θ₀) ⊙ M
其中,M是一个二进制掩码,仅在选定的参数位置为1;γ是一个注入因子,控制新任务信息的注入量;⊙表示逐元素乘法。
理论分析表明,通过适当选择γ,可以在保留预训练知识和获取新任务能力之间达到近似最优的平衡。论文中证明了,通过控制γ的值,可以界限新任务信息对原始模型的影响,从而避免灾难性遗忘。
架构设计与实现
整体架构
AdaDARE-γ的整体架构包含三个核心组件:预训练模型、微调模型和自适应融合模块。其创新之处在于它不重新训练模型,而是智能地融合两个模型的参数。
下面的流程图展示了AdaDARE-γ的完整工作流程:
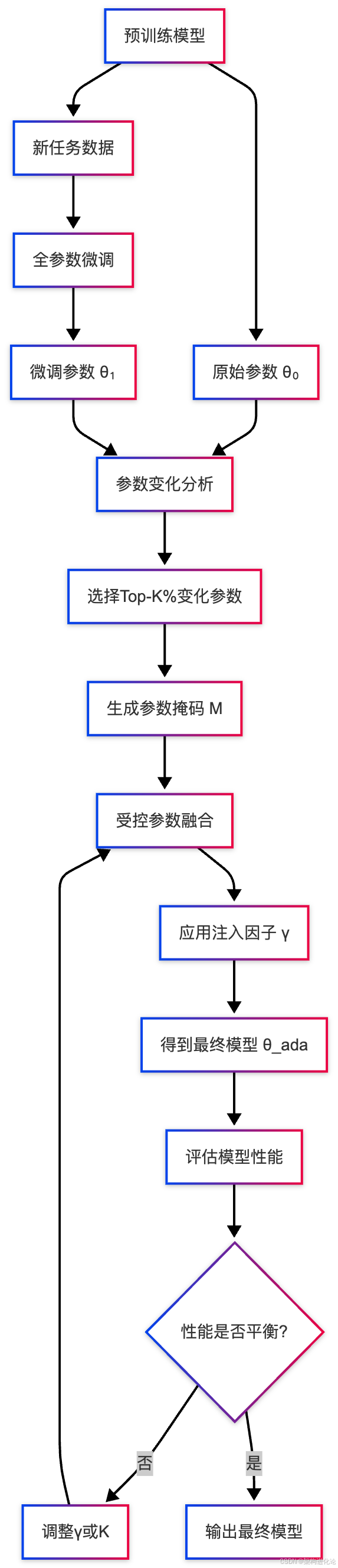
关键算法实现
以下是AdaDARE-γ核心算法的Python实现:
import torch
import torch.nn as nn
from typing import Dict, Tuple, Optional
class AdaDAREGamma:
"""
AdaDARE-γ 算法实现类
通过自适应参数选择和受控注入平衡稳定性和塑性
"""
def __init__(self,
pretrained_model: nn.Module,
injection_factor: float = 0.5,
selection_ratio: float = 0.3):
"""
初始化 AdaDARE-γ
Args:
pretrained_model: 预训练模型
injection_factor: 注入因子γ,控制新知识注入量
selection_ratio: 参数选择比例K%,决定选择多少参数进行更新
"""
self.pretrained_model = pretrained_model
self.gamma = injection_factor
self.k = selection_ratio
# 保存预训练模型的初始参数
self.pretrained_params = {
name: param.data.clone() for name, param in pretrained_model.named_parameters()
}
def select_parameters(self, finetuned_model: nn.Module) -> Dict[str, torch.Tensor]:
"""
选择变化最大的Top-K%参数
Args:
finetuned_model: 完整微调后的模型
Returns:
binary_mask: 二进制掩码,标识哪些参数被选中
"""
param_changes = {}
# 计算每个参数的变化量
for name, param in finetuned_model.named_parameters():
if name in self.pretrained_params:
# 计算参数变化的绝对值
change = torch.abs(param.data - self.pretrained_params[name])
# 对变化量进行平均,得到每个参数的整体变化分数
param_changes[name] = torch.mean(change).item()
# 根据变化量排序参数
sorted_params = sorted(param_changes.items(),
key=lambda x: x[1],
reverse=True)
# 选择Top-K%变化最大的参数
num_select = int(len(sorted_params) * self.k)
selected_params = {name for name, _ in sorted_params[:num_select]}
# 创建二进制掩码
binary_mask = {}
for name, param in finetuned_model.named_parameters():
if name in self.pretrained_params:
# 如果参数被选中,掩码为1,否则为0
mask_value = 1.0 if name in selected_params else 0.0
binary_mask[name] = torch.ones_like(param.data) * mask_value
return binary_mask
def fuse_models(self,
finetuned_model: nn.Module,
binary_mask: Optional[Dict[str, torch.Tensor]] = None) -> nn.Module:
"""
融合预训练模型和微调模型
Args:
finetuned_model: 完整微调后的模型
binary_mask: 参数选择掩码
Returns:
fused_model: 融合后的模型
"""
# 如果没有提供掩码,自动生成
if binary_mask is None:
binary_mask = self.select_parameters(finetuned_model)
# 创建融合模型(复制预训练模型)
fused_model = type(self.pretrained_model)()
fused_model.load_state_dict(self.pretrained_model.state_dict())
# 应用受控参数融合
for name, param in fused_model.named_parameters():
if name in self.pretrained_params and name in binary_mask:
# 计算参数差异
param_diff = finetuned_model.state_dict()[name] - self.pretrained_params[name]
# 应用受控更新: θ_ada = θ₀ + γ · (θ₁ - θ₀) ⊙ M
updated_param = self.pretrained_params[name] + self.gamma * param_diff * binary_mask[name]
param.data.copy_(updated_param)
return fused_model
def evaluate_balance(self,
original_tasks: Dict,
new_tasks: Dict) -> Tuple[float, float]:
"""
评估模型在稳定性和塑性之间的平衡
Args:
original_tasks: 原始任务性能评估数据
new_tasks: 新任务性能评估数据
Returns:
stability_score: 稳定性得分(原始任务保持性能)
plasticity_score: 塑性得分(新任务学习性能)
"""
# 计算原始任务性能保持率
original_performance = self.evaluate_performance(original_tasks)
baseline_performance = self.get_baseline_performance(original_tasks)
stability_score = original_performance / baseline_performance
# 计算新任务学习性能
new_performance = self.evaluate_performance(new_tasks)
full_ft_performance = self.get_full_finetuning_performance(new_tasks)
plasticity_score = new_performance / full_ft_performance
return stability_score, plasticity_score
# 使用示例
def demonstrate_adaDARE():
"""
演示 AdaDARE-γ 的使用方法
"""
# 初始化预训练模型(这里使用简化表示)
pretrained_model = YourMultimodalModel()
# 初始化 AdaDARE-γ
adapter = AdaDAREGamma(
pretrained_model=pretrained_model,
injection_factor=0.6, # 注入因子
selection_ratio=0.4 # 选择40%变化最大的参数
)
# 在新任务数据上全参数微调
finetuned_model = fine_tune_on_new_task(pretrained_model, new_task_data)
# 选择重要参数并融合模型
fused_model = adapter.fuse_models(finetuned_model)
# 评估平衡效果
stability, plasticity = adapter.evaluate_balance(original_tasks, new_tasks)
print(f"稳定性得分: {stability:.2%}") # 论文中达到98.2%
print(f"塑性得分: {plasticity:.2%}") # 论文中达到98.7%
与现有方法的对比
为了清晰展示AdaDARE-γ的优势,我们将其与几种主流方法进行对比:
| 方法 | 稳定性 | 塑性 | 参数效率 | 计算效率 |
|---|---|---|---|---|
| 全参数微调 | 低 | 高 | 低 | 中 |
| 基于正则化的方法 | 中 | 中 | 高 | 高 |
| 经验回放 | 中高 | 中高 | 中 | 低 |
| 参数隔离 | 高 | 中 | 低 | 中 |
| AdaDARE-γ | 高 | 高 | 高 | 高 |
从上表可以看出,AdaDARE-γ在多个维度上都表现出色,尤其是在平衡稳定性和塑性方面实现了最佳效果。
实验分析与结果
实验设置
论文中在InstructBLIP和LLaVA-1.5两个主流多模态大模型上进行了全面实验,任务涵盖图像描述生成和视觉问答等多个领域。评估指标主要包括:
-
稳定性度量:模型在原始任务上性能的保持程度
-
塑性度量:模型在新任务上学到的性能水平
-
平衡分数:综合衡量稳定性和塑性的指标
主要结果
实验结果表明,AdaDARE-γ在保持原始任务性能和学习新任务之间实现了卓越的平衡:
-
在原始任务上保持了98.2%的性能(相比标准微调的显著提升)
-
在新任务上达到了98.7%的标准微调性能
-
在多个数据集和任务上都表现出一致的优越性
这些结果证明了AdaDARE-γ方法的有效性和泛化能力,说明它能够在不牺牲性能的情况下,有效解决灾难性遗忘问题。
消融研究
论文中还进行了系统的消融研究,分析了AdaDARE-γ中各个组件的影响:
-
参数选择比例K%的影响:研究发现,中等比例(30%-50%)通常能实现最佳平衡
-
注入因子γ的影响:γ=0.5-0.7范围内能在稳定性和塑性间达到良好平衡
-
组件贡献分析:自适应参数选择和受控注入两者都对最终性能有重要贡献
实际应用案例
医疗影像诊断系统
考虑一个实际的医疗应用场景:一个已经能够识别肺部X光片中的肺炎症状的多模态模型,现在需要学习识别视网膜图像中的糖尿病视网膜病变。
使用传统微调方法,模型在学习新任务后,可能会丧失准确识别肺炎的能力,这在医疗场景中是极其危险的。而使用AdaDARE-γ方法,可以:
-
保持在肺炎识别上的高准确性(稳定性)
-
有效学习糖尿病视网膜病变的识别(塑性)
-
不需要存储大量患者原始数据,符合隐私保护要求
个性化智能助手
另一个应用场景是个性化智能助手。假设一个已训练好的助手能够理解用户的工作相关查询,现在需要适应某个用户的个人偏好和表达习惯。
使用AdaDARE-γ,助手可以:
-
保持对工作查询的理解能力
-
学习适应用户的个人表达方式
-
避免在适应过程中忘记已掌握的通识知识
未来发展与挑战
尽管AdaDARE-γ取得了显著成果,但多模态大模型的高效适应仍然面临一些挑战:
技术挑战
-
动态调整机制:目前的γ和K是超参数,未来可以研究动态调整机制,根据任务复杂度自动调整这些参数。
-
跨模态差异:不同模态可能需要不同的适应策略,文本和图像模态的稳定性和塑性需求可能不同。
-
可扩展性:随着模型规模不断扩大,参数选择机制的计算效率需要进一步优化。
应用前景
AdaDARE-γ技术为多个领域带来了新的可能性:
-
终身学习系统:能够持续学习新知识而不遗忘旧知识的AI系统
-
个性化AI:能够适应个体用户需求而不丧失通用能力的AI助手
-
资源受限环境:在计算和存储受限的环境中实现模型的高效更新
总结
AdaDARE-γ代表了一种新颖而高效的多模态大模型适应方法,它通过自适应参数选择和受控知识注入,巧妙平衡了稳定性和塑性之间的权衡。这种方法不仅理论上有趣,而且在实际应用中表现出显著优势。
论文的实验结果证实,AdaDARE-γ在多个基准测试中都达到了state-of-the-art水平,为解决灾难性遗忘这一长期挑战提供了有效的解决方案。这一技术的出现,将加速AI系统从静态模型向持续学习的系统演进,使AI能够像人类一样不断积累知识而不遗忘。
随着多模态大模型在各行各业的应用日益广泛,像AdaDARE-γ这样的高效适应技术将发挥越来越重要的作用,为实现真正智能的、可持续学习的AI系统铺平道路。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










