二叉树，二叉查找树的搜索，插入，删除

树

树是元素的集合，每棵树由多个节点）组成，用以储存元素。某些节点之间存在着一定的关系，用连线表示，连线称为边或者链接。边的上端点成为父节点，下端称为子节点。
最顶端的称为根节点，其他没有子节点的节点称为叶子节点或者叶节点。

总结

	一个树是元素的集合。
	一个树可以为空，即没有元素，此时这个树称为空树。
	如果一个树有元素。那么根节点与其子树的根节点的连接叫做边或者称为链接。

特征：
高度，深度

节点高度：是自下到上的数，节点到叶子结点的最长路径，（从1开始）
节点深度：是自上到下的数，根节点到叶节点的长度。（从1开始）
二叉树的高度：节点高度；
二叉树的深度：左右树中的深度最大值+1

二叉树

：
二叉树只有两个叉，也就是两个子节点：左子节点和右子节点。

如图二这种称为满二叉树，满二叉树即除了最下增的叶节点无子节点外，其余节点都存在，即他的总节点数为

			n=2^m-1，m为节点深度，n为当前深度满节点。

如图三这种为完全二叉树，

所有叶子节点都出现在 k 或者 k-1 层，而且从 1 到 k-1 层必须达到最大节点数；

第 k 层可以不是满的，但是第 k 层的所有节点必须集中在最左边。。

满二叉树一定是完全二叉树，但是完全二叉树不一定是满二叉树

二叉树的三种遍历方法

如图

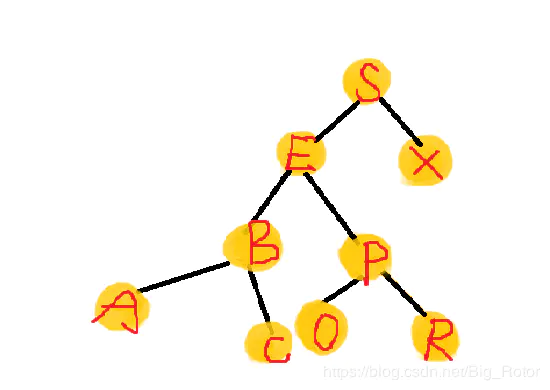
前序遍历：若二叉树为空，则空操作，否则，对于二叉树中的任意节点，先访问这个节点，然后再访问它的左子树，最后打印它的右子树。
即

		S-E-B-A-C-P-O-R-X

中序遍历：若二叉树为空，则空操作，否则，对于二叉树中的任意节点，先访问这个左子树，再访问这个节点，最后打印他的右子树。
即

	A-B-C-E-O-P-R-S-X

后序遍历：若二叉树为空，则空操作，否则，对于二叉树中的任意节点，先访问它的左子树，然后访问它的右子树，最后访问这个节点本身。
即

A-C-B-O-R-P-E-X-S

二叉查找树

是一种特殊的二叉树，每个节点的值要大于左子树的任意节点，而小于右子树的任意节点。

查找

如图
假设我们要查找节点R

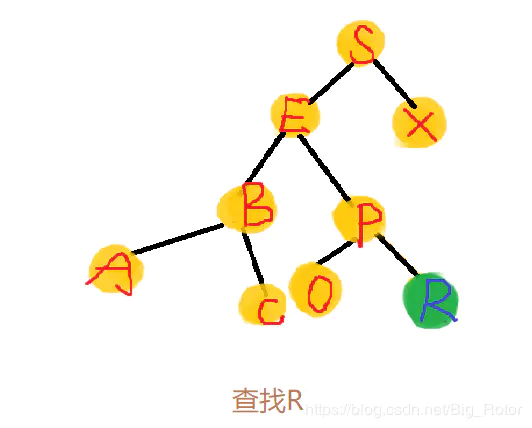
方法

	如果二叉查找树为空，则返回空操作，否则，执行下个操作；
   先取根节点，如果节点 X 等于根节点，则返回；
   如果节点小于根节点，则递归查找左子树；
   如果节点大于根节点，则递归查找右子树。

总结

	先判断是否为空，然后和根节点比较，比根节点大就去右子树查找，比根节点小就去左子树查找。

插入

如图

加入要插入M，

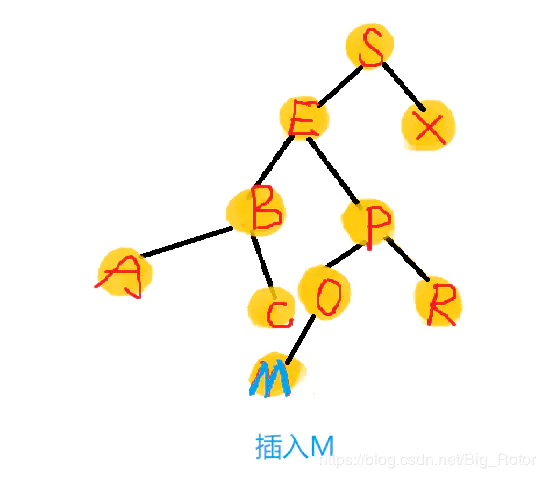
方法

如果树是空的，则直接将新节点插入，否则，执行下面步骤。
要插入的数据比根节点数据大，则到右子树中插入新数据，如果右子树为空，则将新数据直接插入到右子节点的位置；不为空，则继续遍历右子树，查找插入位置。
要插入的数据比根节点数据小，则到左子树中插入数据，如果左子树为空，则直接将新数据插入到左子节点的位置；不为空，则继续遍历左子树，查找插入的位置。

总结

	和查找一样，先判断是否为空，如果为空就直接插入，如果非空就进行比较，如果比根节点大，
	就去右子树插入数据，如果右子树空的就直接插入，如果非空就继续遍历，直到插入。如果比
	根节点小，就在左子树进行如是操作

删除

如图
加入要删除 13,18 55

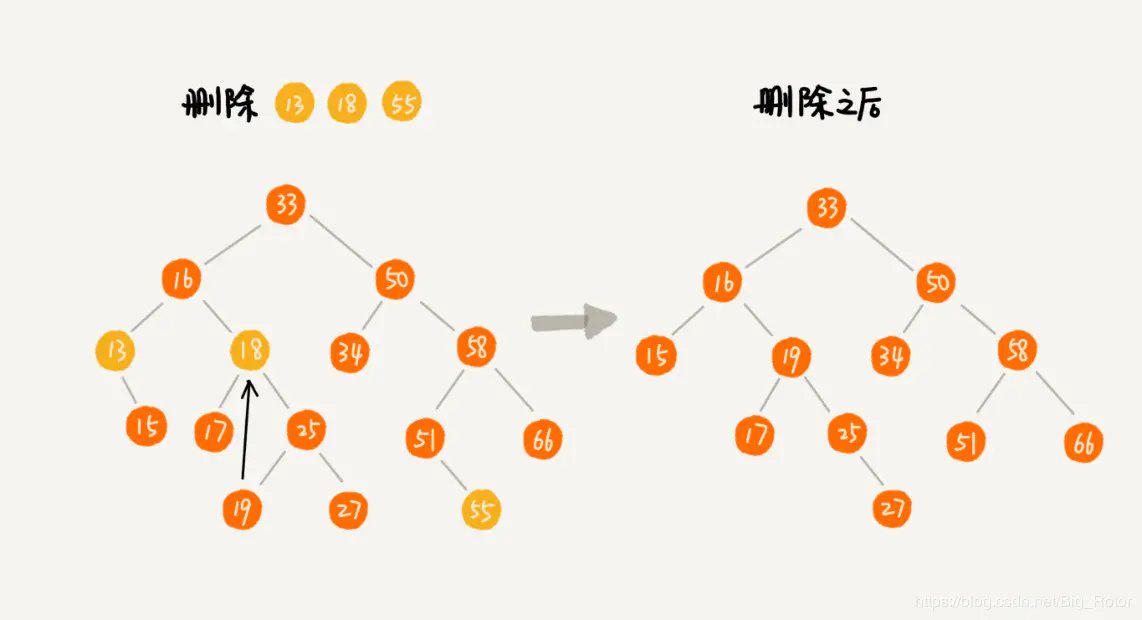
方法

	第一种情况，如果要删除的节点没有子节点，直接将父节点指向要删除节点的指针指向 null。
	比如途中要删除的节点 55。
	第二种情况，如果要删除的节点只有一个节点，即只有左子节点或右子节点，
	则将父节点指向要删除节点的指针指向要删除节点的子节点即可。比如途中要删除的节点13。
	第三种情况，如果要删除的节点有两个子节点，
	则需要先找到这个节点右子树中的最小节点或者左子树中的最大节点，将其替换到要删除的节点	上。	
	然后删除这个右子树中的最小节点或左子树中的最大节点，这样就可以利用
	1、2 两条规则来删除了。比如图中要删除的节点 18。

总结：

	遇到有俩子节点的，就找左边最大的或者右边最小的替换掉那个节点，然后把原来的删掉就可以