1.自动微分
自动微分模块torch.autograd负责自动计算张量操作的梯度,具有自动求导功能。自动微分模块是构成神经网络训练的必要模块,可以实现网络权重参数的更新,使得反向传播算法的实现变得简单而高效。
1. 基础概念
-
张量
Torch中一切皆为张量,属性requires_grad决定是否对其进行梯度计算。默认是 False,如需计算梯度则设置为True。
-
计算图:
torch.autograd通过创建一个动态计算图来跟踪张量的操作,每个张量是计算图中的一个节点,节点之间的操作构成图的边。
在 PyTorch 中,当张量的 requires_grad=True 时,PyTorch 会自动跟踪与该张量相关的所有操作,并构建计算图。每个操作都会生成一个新的张量,并记录其依赖关系。当设置为
True时,表示该张量在计算图中需要参与梯度计算,即在反向传播(Backpropagation)过程中会自动计算其梯度;当设置为False时,不会计算梯度。
叶子节点:
在 PyTorch 的自动微分机制中,叶子节点(leaf node) 是计算图中:
-
由用户直接创建的张量,并且它的 requires_grad=True。
-
这些张量是计算图的起始点,通常作为模型参数或输入变量。
特征:
-
没有由其他张量通过操作生成。
-
如果参与了计算,其梯度会存储在 leaf_tensor.grad 中。
-
默认情况下,叶子节点的梯度不会自动清零,需要显式调用 optimizer.zero_grad() 或 x.grad.zero_() 清除。
-
如何判断一个张量是否是叶子节点?
通过 tensor.is_leaf 属性,可以判断一个张量是否是叶子节点。
-
import torch x = torch.tensor([1, 2, 3], dtype=torch.float, requires_grad=True) y = x ** 2 z = y ** 2 print(x.is_leaf) print(y.is_leaf) print(z.is_leaf) -
反向传播
使用tensor.backward()方法执行反向传播,从而计算张量的梯度。这个过程会自动计算每个张量对损失函数的梯度。例如:调用 loss.backward() 从输出节点 loss 开始,沿着计算图反向传播,计算每个节点的梯度。
-
梯度
计算得到的梯度通过tensor.grad访问,这些梯度用于优化模型参数,以最小化损失函数。
2. 计算梯度
使用tensor.backward()方法执行反向传播,从而计算张量的梯度
2.1 标量梯度计算
import torch
# 定义一个标量,注意需要浮点型,也可以设置dtype为torch.float
x = torch.tensor(1.0, requires_grad=True)
y = x**2
# 反向传播
y.backward()
# 查看梯度
print(x.grad)
2.2 向量梯度计算
# 向量梯度计算
x = torch.tensor([1, 2, 3], dtype=torch.float, requires_grad=True)
# y = x**2
# y.backward()
# print(x.grad)
'''
错误预警:RuntimeError: grad can be implicitly created only for scalar outputs
由于 *y* 是一个向量,我们需要提供一个与 *y* 形状相同的向量作为 backward() 的参数,这个参数通常被称为
**梯度张量**(gradient tensor),它表示 *y* 中每个元素的梯度。
'''
y = x ** 2
y.backward(torch.ones_like(x))
print(x.grad)我们也可以将向量 y 通过一个标量损失函数(如 y.mean())转换为一个标量,反向传播时就不需要提供额外的梯度向量参数了。这是因为标量的梯度是明确的,直接调用 .backward() 即可。
x = torch.tensor([1, 2, 3], dtype=torch.float, requires_grad=True)
y = x ** 2
loss = y.sum()
loss.backward()
print(x.grad)调用 loss.backward() 从输出节点 loss 开始,沿着计算图反向传播,计算每个节点的梯度。
2.3 多标量梯度计算
# 多标量梯度计算
x = torch.tensor(1.0, requires_grad=True)
y = torch.tensor(2.0, requires_grad=True)
z = x**2 + y**2
z.backward()
print(x.grad, y.grad)
2.4 多向量梯度计算
# 多向量梯度计算
x = torch.tensor([1, 2, 3], dtype=torch.float, requires_grad=True)
y = torch.tensor([4, 5, 6], dtype=torch.float, requires_grad=True)
z = x ** 2 + y ** 2 + 10
loss = z.sum()
loss.backward()
print(x.grad, y.grad)3. 梯度上下文控制
梯度计算的上下文控制和设置对于管理计算图、内存消耗、以及计算效率至关重要。下面我们学习下Torch中与梯度计算相关的一些主要设置方式。
3.1 控制梯度计算
梯度计算是有性能开销的,有些时候我们只是简单的运算,并不需要梯度
# 控制梯度计算
x = torch.tensor(2.1, requires_grad=True)
y = x**2 + 1
# 默认为true
print(y.requires_grad)
# 1.通过with torch.no_grad方法
with torch.no_grad():
y = x**2 + 1
print(y.requires_grad)
# 2.通过装饰器
@torch.no_grad()
def func(x):
return x**2 + 1
y = func(x)
print(y.requires_grad)
# 3.设置全局控制,需谨慎
torch.set_grad_enabled(False)
y = x**2 + 1
print(y.requires_grad)
3.2 累计梯度
默认情况下,当我们重复对一个自变量进行梯度计算时,梯度是累加的
x = torch.tensor([1, 2, 3], dtype=torch.float, requires_grad=True)
# 梯度如果不清零,会累加在上一次的数据上
for i in range(3):
y = x ** 2 + 2 * x + 7
z = y.sum()
z.backward()
print(x.grad)
# tensor([4., 6., 8.])
# tensor([ 8., 12., 16.])
# tensor([12., 18., 24.])3.3 梯度清零
for i in range(3):
y = x ** 2 + 2 * x + 7
z = y.sum()
z.backward()
print(x.grad)
# 每次清零梯度
x.grad.zero_()
# tensor([4., 6., 8.])
# tensor([4., 6., 8.])
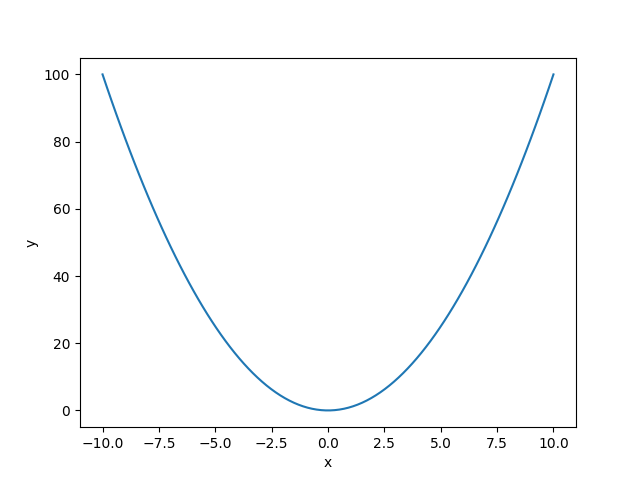
# tensor([4., 6., 8.])3.4 案例1-求函数最小值
通过梯度下降找到函数最小值,通过梯度帮我们寻找最小值。
# 寻找函数的最小值
import numpy as np
from matplotlib import pyplot as plt
import torch
# 画出图像
x = np.linspace(-10, 10, 100)
y = x**2
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
# 通过反向传播寻找最小值
list = []
# 初始化一个值
x = torch.tensor(3.0, requires_grad=True)
# 设置学习次数,和学习率
epochs = 50
lr = 0.1
for epoch in range(epochs):
y = x ** 2
# 反向传播,寻找梯度
y.backward()
# 梯度下降时,x不需要参加梯度计算
with torch.no_grad():
x -= lr * x.grad
x.grad.zero_()
print(f'epoch: {epoch}, x:{x.item():.4f}, y:{y.item():.4f}')
list.append((x.item(),y.item()))
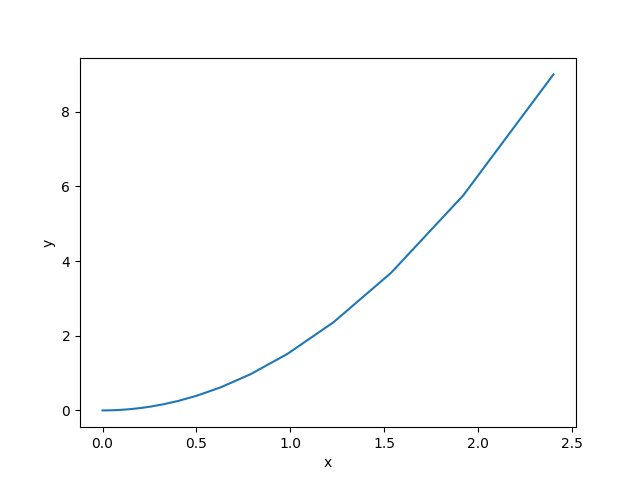
# 可视化寻找最小值
lis_x = [l[0] for l in list]
lis_y = [l[1] for l in list]
plt.plot(lis_x, lis_y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
epoch: 0, x:2.4000, y:9.0000
epoch: 1, x:1.9200, y:5.7600
epoch: 2, x:1.5360, y:3.6864
epoch: 3, x:1.2288, y:2.3593
epoch: 4, x:0.9830, y:1.5099
epoch: 5, x:0.7864, y:0.9664
epoch: 6, x:0.6291, y:0.6185
epoch: 7, x:0.5033, y:0.3958
epoch: 8, x:0.4027, y:0.2533
epoch: 9, x:0.3221, y:0.1621
epoch: 10, x:0.2577, y:0.1038
epoch: 11, x:0.2062, y:0.0664
epoch: 12, x:0.1649, y:0.0425
epoch: 13, x:0.1319, y:0.0272
epoch: 14, x:0.1056, y:0.0174
epoch: 15, x:0.0844, y:0.0111
epoch: 16, x:0.0676, y:0.0071
epoch: 17, x:0.0540, y:0.0046
epoch: 18, x:0.0432, y:0.0029
epoch: 19, x:0.0346, y:0.0019
epoch: 20, x:0.0277, y:0.0012
epoch: 21, x:0.0221, y:0.0008
epoch: 22, x:0.0177, y:0.0005
epoch: 23, x:0.0142, y:0.0003
epoch: 24, x:0.0113, y:0.0002
epoch: 25, x:0.0091, y:0.0001
epoch: 26, x:0.0073, y:0.0001
epoch: 27, x:0.0058, y:0.0001
epoch: 28, x:0.0046, y:0.0000
epoch: 29, x:0.0037, y:0.0000
epoch: 30, x:0.0030, y:0.0000
epoch: 31, x:0.0024, y:0.0000
epoch: 32, x:0.0019, y:0.0000
epoch: 33, x:0.0015, y:0.0000
epoch: 34, x:0.0012, y:0.0000
epoch: 35, x:0.0010, y:0.0000
epoch: 36, x:0.0008, y:0.0000
epoch: 37, x:0.0006, y:0.0000
epoch: 38, x:0.0005, y:0.0000
epoch: 39, x:0.0004, y:0.0000
epoch: 40, x:0.0003, y:0.0000
epoch: 41, x:0.0003, y:0.0000
epoch: 42, x:0.0002, y:0.0000
epoch: 43, x:0.0002, y:0.0000
epoch: 44, x:0.0001, y:0.0000
epoch: 45, x:0.0001, y:0.0000
epoch: 46, x:0.0001, y:0.0000
epoch: 47, x:0.0001, y:0.0000
epoch: 48, x:0.0001, y:0.0000
epoch: 49, x:0.0000, y:0.0000
3.5 案例2-函数参数求解
让计算机自己解函数。通过梯度下降,回归寻求解。
import numpy as np
import torch
def linear_regression():
x = torch.tensor([1, 3, 5, 7, 9], dtype=torch.float)
y = torch.tensor([7, 13, 19, 25, 31], dtype=torch.float)
# 真实线性y=3x+4
# 初始化权重,截距a,b,requires_grad参与梯度计算
a = torch.tensor([0], dtype=torch.float, requires_grad=True)
b = torch.tensor([1], dtype=torch.float, requires_grad=True)
print(a.is_leaf)
# 训练次数
epochs = 500
# 学习率
lr = 0.01
# 开始训练
for epoch in range(epochs):
# 预测值
y_pred = a * x + b
# 计算损失,使用均方误差
loss = ((y_pred - y) ** 2).mean()
# 反向传播
loss.backward()
# 梯度下降
with torch.no_grad():
a -= lr * a.grad
b -= lr * b.grad
a.grad.zero_()
b.grad.zero_()
if epoch % 10 == 0:
print(f'epoch:{epoch},损失: {loss.item()}')
print(f'真实值:{y},预测值:{y_pred}')
print(f'权重:{a},截距:{b}')
True
epoch:0,损失: 396.0
epoch:10,损失: 1.3608119487762451
epoch:20,损失: 1.2374820709228516
epoch:30,损失: 1.1253283023834229
epoch:40,损失: 1.0233395099639893
epoch:50,损失: 0.930594265460968
epoch:60,损失: 0.8462547063827515
epoch:70,损失: 0.7695580720901489
epoch:80,损失: 0.6998127102851868
epoch:90,损失: 0.6363885402679443
epoch:100,损失: 0.5787128210067749
epoch:110,损失: 0.5262640118598938
epoch:120,损失: 0.47856825590133667
epoch:130,损失: 0.43519601225852966
epoch:140,损失: 0.39575430750846863
epoch:150,损失: 0.3598865270614624
epoch:160,损失: 0.3272702693939209
epoch:170,损失: 0.2976093888282776
epoch:180,损失: 0.27063724398612976
epoch:190,损失: 0.24610932171344757
epoch:200,损失: 0.22380438446998596
epoch:210,损失: 0.2035212516784668
epoch:220,损失: 0.18507592380046844
epoch:230,损失: 0.16830237209796906
epoch:240,损失: 0.1530487835407257
epoch:250,损失: 0.13917794823646545
epoch:260,损失: 0.12656426429748535
epoch:270,损失: 0.11509381234645844
epoch:280,损失: 0.10466273128986359
epoch:290,损失: 0.09517727792263031
epoch:300,损失: 0.08655142784118652
epoch:310,损失: 0.07870719581842422
epoch:320,损失: 0.07157392799854279
epoch:330,损失: 0.06508719176054001
epoch:340,损失: 0.05918840691447258
epoch:350,损失: 0.05382417514920235
epoch:360,损失: 0.048946063965559006
epoch:370,损失: 0.04451027885079384
epoch:380,损失: 0.04047613590955734
epoch:390,损失: 0.036807890981435776
epoch:400,损失: 0.033471863716840744
epoch:410,损失: 0.030438238754868507
epoch:420,损失: 0.027679655700922012
epoch:430,损失: 0.025170985609292984
epoch:440,损失: 0.02288980409502983
epoch:450,损失: 0.020815392956137657
epoch:460,损失: 0.01892876997590065
epoch:470,损失: 0.017213305458426476
epoch:480,损失: 0.015653256326913834
epoch:490,损失: 0.014234600588679314
真实值:tensor([ 7., 13., 19., 25., 31.]),预测值:tensor([ 6.8033, 12.8741, 18.9450, 25.0159, 31.0867], grad_fn=<AddBackward0>)
权重:tensor([3.0353], requires_grad=True),截距:tensor([3.7689], requires_grad=True)






















 1640
1640

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








