其实我线性代数考试每次都99,100的,可惜好久不学都快忘了。
没想到acm居然要用到,早知道不扔笔记本了QAQ
#define A(n,m) n行m列的行列式A
#define A[n][m] 行列式A的第n行第m列的元素
#define |A| 行列式A的值
行列式A=[322514322]\begin{bmatrix} 3&2&2\\5&1&4\\3&2&2 \end{bmatrix}⎣⎡353212242⎦⎤ , 312为主对角线 , 213为副对角线 , |A|为主对角线方向相乘 - 副对角线反向相乘 : 6+24+20-6-20-24=0
  \\\;
两个行列式A(a,b),B(c,d)A(a,b),B(c,d)A(a,b),B(c,d)可乘当且仅当b=cb=cb=c,乘完后的行列式为C(a,d)C(a,d)C(a,d),且C[i][j]=A的第i行×B的第j列C[i][j]=A的第i行\times B的第j列C[i][j]=A的第i行×B的第j列
  \\\;
矩阵或行列式的一行或一列称为向量
  \\\;
A(a,b)TA(a,b)^TA(a,b)T表示A(a,b)A(a,b)A(a,b)的转置, ->AT(b,a)    A[i][j]=AT[j][i]A^T(b,a) \;\;A[i][j]=A^T[j][i]AT(b,a)A[i][j]=AT[j][i]
  \\\;
一个矩阵的秩 r 的定义为 : 至少r个行向量才能表示矩阵中任意一个行向量
\quad\quad比如 : (1,0,0)和(0,1,0)就可以表示(2,3,0)
\quad\quad所以r最大为min(n,m)
  \\\;
E表示单位矩阵,主对角线为1其他为0
  \\\;
A−1表示A的逆,A−1×A=EA^{-1}表示A的逆,A^{-1}\times A=EA−1表示A的逆,A−1×A=E
求A−1A^{-1}A−1方法 : 把A和单位矩阵并排写在一起,化解A至单位矩阵,右边的单位矩阵变幻后即为A的逆
  \\\;
  \\\;
有如下方程组 :

矩阵形式为 :
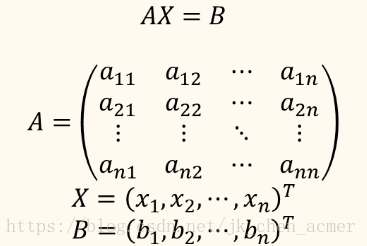
A称为系数矩阵, B放到A的右边连在一起称为增广矩阵
  \\\;
B̸=0时:B\not=0时 :B̸=0时: 称此方程组为非齐次线性方程组
方程组有唯一解⇔∣A∤=0\Leftrightarrow |A|\not=0⇔∣A∤=0 ⇔\Leftrightarrow⇔ A可逆
方程组有解⇔\Leftrightarrow⇔ r(系数矩阵)=r(增广矩阵)
B̸=0时:B\not=0时 :B̸=0时: 称此方程组为齐次线性方程组
方程组有唯一解且为全0解⇔∣A∤=0\Leftrightarrow |A|\not=0⇔∣A∤=0 ⇔\Leftrightarrow⇔ A可逆
方程组有非0解⇔∣A∣=0⇔\Leftrightarrow |A|=0\Leftrightarrow⇔∣A∣=0⇔ A不可逆
  \\\;
  \\\;
初等变换 :
交换两行 , 一行乘上一个非0数 , 一行加上另一行的k倍
高斯消元 :
通过初等变换将系数矩阵变成上三角矩阵 , 再变成单位矩阵 , 此时的B就是对应x的解

上图的解为 : x1=9,x2=−1,x3=−6x_1=9,x_2=-1,x_3=-6x1=9,x2=−1,x3=−6
const double EPS=1e-8;
//高斯消元,系数矩阵为a[i][j],i=1…n,j=1…n,常数为a[i][n+1],i=1…n,答案存在x[i]
double x[maxn], a[maxn][maxn];
void guass(int n) {
for(int i=1;i<=n;i++) {
int j = -1;
for(int k=i;k<=n;k++) {
if (abs(a[k][i])>EPS) {
j=k; break;
}
}
if (j==-1) continue;
if (i!=j) for(int k=i;k<=n+1;k++) swap(a[i][k], a[j][k]);
for(int k=i+1;k<=n;k++) {
double x = a[i][i], y = a[k][i];
if (abs(y) < EPS) continue;
for(int p=i;p<=n+1;p++) {
a[k][p] = a[i][p] - x / y * a[k][p];
}
}
}
for(int i=n;i>=1;i--) {
double tmp = 0;
for(int j=i+1;j<=n;j++) {
tmp += a[i][j] * x[j];
}
tmp = a[i][n+1] - tmp;
if (abs(a[i][i])>EPS)
x[i] = tmp / a[i][i];
else {
}
}
}
范德蒙德行列式

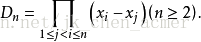







 本文回顾了线性代数的基本概念,如行列式、矩阵运算、向量、秩、逆矩阵及高斯消元法。强调了这些知识在ACM竞赛中的重要性,并提供了行列式的计算方法、矩阵乘法原则、向量表示、矩阵秩的理解、逆矩阵的求解过程以及方程组的解决技巧。
本文回顾了线性代数的基本概念,如行列式、矩阵运算、向量、秩、逆矩阵及高斯消元法。强调了这些知识在ACM竞赛中的重要性,并提供了行列式的计算方法、矩阵乘法原则、向量表示、矩阵秩的理解、逆矩阵的求解过程以及方程组的解决技巧。
















 1794
1794

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








