杨辉三角

最新推荐文章于 2024-11-26 13:57:15 发布

原创最新推荐文章于 2024-11-26 13:57:15 发布 · 1.5k 阅读

0 ·

CC 4.0 BY-SA版权

本文介绍了一种使用C++编程语言实现杨辉三角的方法，包括递推公式和通项公式的应用，并提供了一个完整的代码示例。通过定义组合数的计算方式，实现了杨辉三角中任一位置元素值的有效计算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

设 F(i,j)为第i行第j个元素

看图找规律：
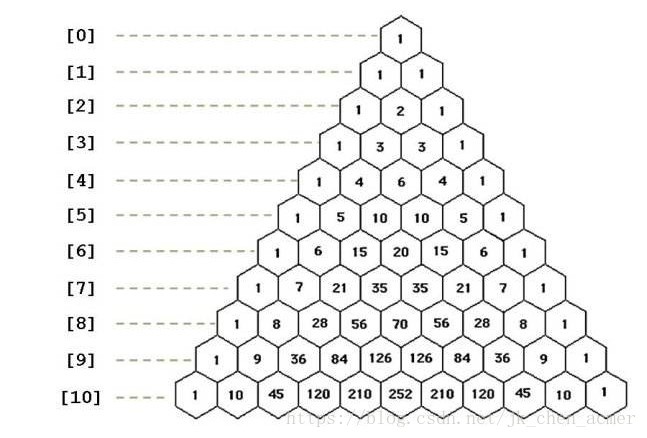
这里写图片描述

首先当然是性质了，首尾两个元素规定是1，其他的数是顶上两个数的和
然后每个数都可以从15，20，35看出，每个数都是一个排列数

递推公式：F(i,j)=F(i-1,j-1)+F(i-1,j)
通项公式：F(i,j)=C(i-1,j-1) (i-1下，j-1上)

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<algorithm>
#include<set>
#include<map>
#include<list>
#include<vector>
#include<stack>
#include<queue>
#include<ctime>
#include<cstdlib>
#include<sstream>
#include<functional>
#define D long long
#define MAX 0x7fffffff
#define MIN -0x7fffffff
#define mmm(a,b) memset(a,b,sizeof(a))
#define for1(i,a,b) for(int i=a;i<=b;i++)
#define for2(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
#define N 1001000
#define MOD (D)((int)1e9+7)
#define mod (D)((int)1e9+7)
const double pi=acos(-1);
D read(){ D ans=0; char last=' ',ch=getchar();
while(ch<'0' || ch>'9')last=ch,ch=getchar();
while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
if(last=='-')ans=-ans; return ans;
}

D swift(D a,D b){
    D ans=1ll;
    while(b){
        if(b%2)ans=ans*a%mod;
        b>>=1;
        a=a*a%mod;
    }return ans;
}
D inv(D a){return swift(a,mod-2);}
D fac[N*3];
void init_fac(){
    fac[0]=fac[1]=1ll;
    for(int i=2;i<=2*N;i++)fac[i]=fac[i-1]*i%mod;
}
D C(D a,D b){//组合数 a下
    if(b>a||b<0)return 0;
    return fac[a]*inv(fac[b])%mod*inv(fac[a-b])%mod;
}
D F(D n,D m){
    return C(n-1,m-1);
}
int main(){
    init_fac();
    D n,m;
    while(cin>>n>>m){
        cout<<F(n,m)<<endl;
    }
}