矩阵快速幂

最新推荐文章于 2025-06-01 00:01:08 发布

原创最新推荐文章于 2025-06-01 00:01:08 发布 · 1.1k 阅读

0 ·

CC 4.0 BY-SA版权

ACM中的数学问题合集专栏收录该内容

44 篇文章

订阅专栏

矩阵应用

线性代数的内容，应该是学计算机的必修课，就不多讲内容了，主要是在编程时的用法。

单项递推

有数列 $A [n] = 4 * A [n - 1] + 2$ ，我们可以写出两个矩阵

项矩阵： ${A[1],1}$
乘积矩阵： ${4,0\} \{2,1\}$

把项矩阵乘一次乘积矩阵，得到了 ${4*A[1]+2,1\}$ 也就是 ${A[2],1\}$ ，所以 $A [n]$ 只要项矩阵乘 $n - 1$ 次就可以得到。

多项递推

举个例子，斐波那契数列 $F [n] = F [n - 1] + F [n - 2]$
因为一个递推式有3项了，所以我们也要扩展一下项矩阵

项矩阵： ${F[1]\}\{F[0]\}$
乘积矩阵： ${1,1\}\{1,0\}$

乘一次(项矩阵左乘乘积矩阵)得 ${F[1]+F[0]\}\{F[1]\}$ 即 ${F[2]\}\{F[1]\}$

矩阵的代码实现

快速幂同 $i n t$ 的快速幂

#include<stdio.h>
#include<string.h>
#define LL long long
#define maxn 109

const LL mod = 1e9+7;
const int SIZE=5;
struct matrix{
	LL mat[SIZE][SIZE];
	matrix(){memset(mat,0,sizeof mat);}
	matrix operator * (const matrix & x)const{
		matrix ans;
		for(int i=0;i<SIZE;i++){
			for(int j=0;j<SIZE;j++){
				for(int k=0;k<SIZE;k++){
					ans.mat[i][j]=(ans.mat[i][j]+mat[i][k]*x.mat[k][j])%mod;
				}
			}
		}
		return ans;
	}
} ;
matrix Pow(matrix a,int b){
	matrix ans;
	for(int i=0;i<SIZE;i++)ans.mat[i][i]=1;
	while(b){
		if(b&1)ans=ans*a;
		a=a*a;
		b>>=1;
	}
	return ans;
}

int main(){
    matrix a,b;
    a.mat[0][0]=1;a.mat[0][1]=2;
    a=a*b;
    a=Pow(a,20);
    printf("%lld\n",a.mat[0][0]);
}

例题one

zjnu 1697

求斐波那契数列第n项

#include<stdio.h>
#include<string.h>
#define D long long
#define N 5
#define MOD ((int)1e4+7)
struct matrix{
	int size;
	D mat[N][N];
	matrix(int s){
		size=s;memset(mat,0,sizeof(mat));
	}void init(){
		for(int i=1;i<=size;i++){
			for(int j=1;j<=size;j++){
				scanf("%lld",&mat[i][j]);
			}
		}
	}void out(){
		for(int i=1;i<=size;i++){
			for(int j=1;j<=size;j++){
				printf("%lld ",mat[i][j]);
			}printf("\n");
		}
	}matrix operator * (const matrix & x)const{
		matrix ans(x.size);
		for(int i=1;i<=x.size;i++){
			for(int j=1;j<=x.size;j++){
				for(int k=1;k<=x.size;k++){
					ans.mat[i][j]=(ans.mat[i][j]+mat[i][k]*x.mat[k][j])%MOD;
				}
			}
		}return ans;
	}
} ;
matrix swift(matrix a,int t){
	matrix ans(a.size);
	for(int i=1;i<=a.size;i++)ans.mat[i][i]=1;
	while(t){
		if(t&1)ans=ans*a;
		a=a*a;t>>=1;
	}return ans;
}

int main(){
	int t;scanf("%d",&t);
	while(t--){
		int n;scanf("%d",&n);
		matrix mul(2),ans(2);
		mul.mat[1][1]=1;mul.mat[1][2]=1;mul.mat[2][1]=1;mul.mat[2][2]=0;
		ans.mat[1][1]=1;ans.mat[2][1]=1;
		ans=swift(mul,n-1)*ans;
		printf("%lld\n",ans.mat[2][1]);
	} 
}

例题two

原题：zjnu 1265

题意：

给n个硬币排成一排，求有3个及以上朝向相同的排列数
a3=2,a4=6…

解析：

找规律，若n个硬币时不符合要求的有bn，有b2=4,b3=6,b4=10 --> bn=b(n-1)+b(n-2)
得：an=2^n-bn
则有

an=2^n-bn
a(n-1)=2^(n-1)-b(n-1)
a(n-2)=2^(n-2)-b(n-2)

(2)+(3)得: a(n-1)+a(n-2)=2^n-2(n-2)-b(n-1)-b(n-2)
–> a(n-1)+a(n-2)=2^n-2(n-2)-bn
–> a(n-1)+a(n-2)=an-2^(n-2)

得出an通项： $an=a(n-1)+a(n-2)+2^(n-2)$

构造矩阵
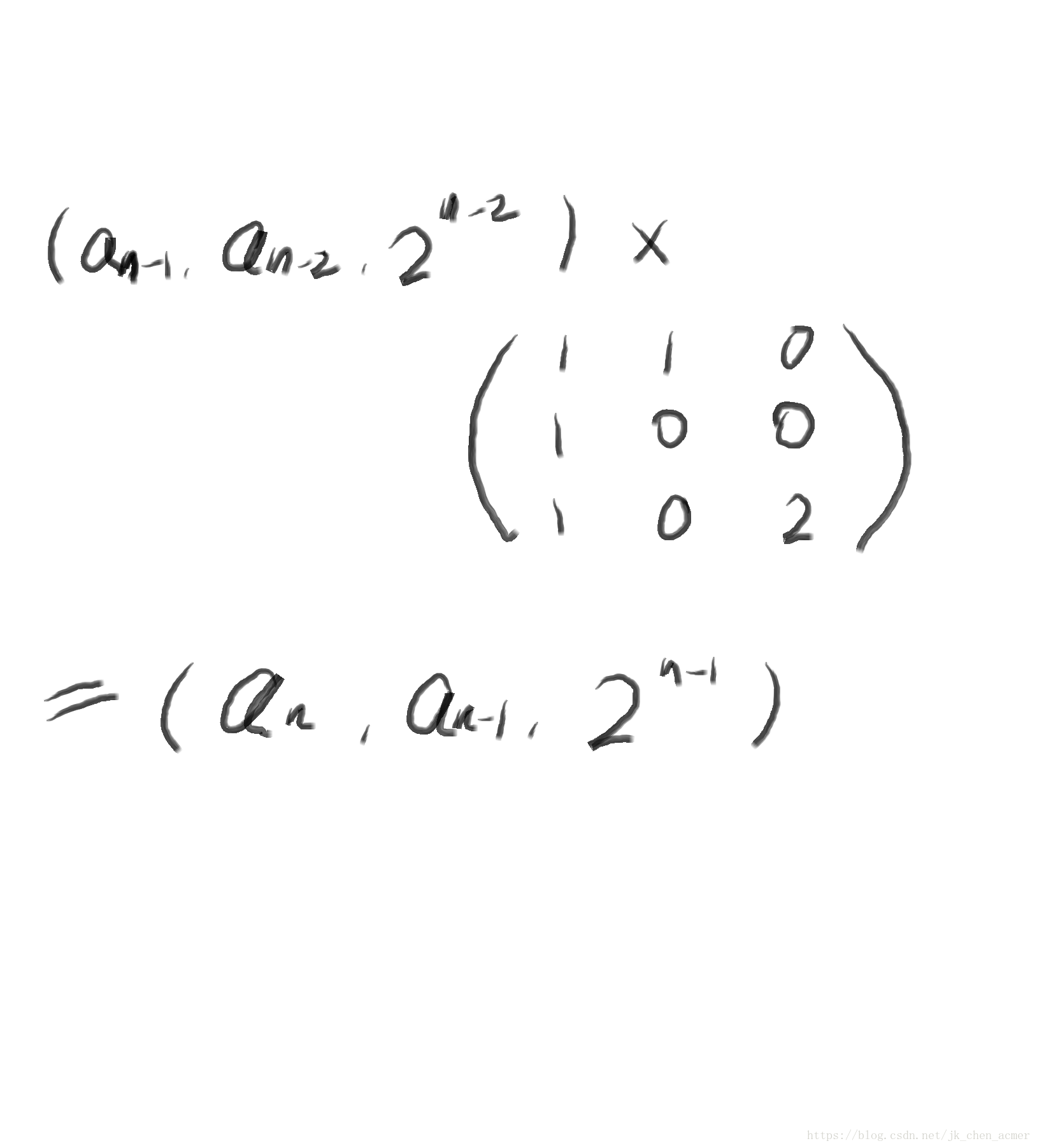
这里写图片描述

代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#define D long long
#define N 109
#define MOD ((int)1e4+7)
using namespace std;
struct matrix{
	int size;
	D mat[N][N];
	matrix(int s){
		size=s;memset(mat,0,sizeof(mat));
	}void init(){
		for(int i=1;i<=size;i++){
			for(int j=1;j<=size;j++){
				scanf("%lld",&mat[i][j]);
			}
		}
	}void out(){
		for(int i=1;i<=size;i++){
			for(int j=1;j<=size;j++){
				printf("%lld ",mat[i][j]);
			}printf("\n");
		}
	}matrix operator * (const matrix & x)const{
		matrix ans(x.size);
		for(int i=1;i<=x.size;i++){
			for(int j=1;j<=x.size;j++){
				for(int k=1;k<=x.size;k++){
					ans.mat[i][j]=(ans.mat[i][j]+mat[i][k]*x.mat[k][j])%MOD;
				}
			}
		}return ans;
	}
} ;

matrix swift(matrix a,int t){
	matrix ans(a.size);
	for(int i=1;i<=a.size;i++)ans.mat[i][i]=1;
	while(t){
		if(t&1)ans=ans*a;
		a=a*a;t>>=1;
	}return ans;
}

D swift(D a,D mul){
    D re=1,base=a;
    while(mul){
        if(mul&1)
        re=re*base%MOD;
        base=base*base%MOD;
        mul>>=1;
    }
    return re;
}

int main(){
	matrix a(3),b(3),c(3);
	a.mat[1][1]=2,a.mat[1][2]=0,a.mat[1][3]=4;
	b.mat[1][1]=1,b.mat[1][2]=1,b.mat[2][1]=1,b.mat[3][1]=1,b.mat[3][3]=2;
	D n;cin>>n;
	a=a*swift(b,n-3);
	printf("%lld\n",a.mat[1][1]);
}