题目
给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,
假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。
输入格式:
输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间
用1空格分隔。
输出格式:
按照"{ v1 v2 … vk }"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
代码
#include <iostream>
#include <queue>
#define MaxVertexNum 10 //最大顶点数设为100
using namespace std;
using Vertex=int; // 用顶点下标表示顶点,为整型
using WeightType = int; //定义权重类型为int
//图
class Graph {
public:
int Nv; // 顶点数
int Ne; // 边数
WeightType G[MaxVertexNum][MaxVertexNum]; // 邻接矩阵
bool* Visited; //标志是否访问过
public:
Graph(int VertexNum); //带参构造函数
void InsertEdge(Vertex V1, Vertex V2); //插入边
void DFS(Vertex V); //DFS
void BFS(Vertex V); //BFS
void Init_Visited(); //将Visited全部变为false
};
int main() {
int Num_of_Node, Num_of_Edge; //顶点数、边数
Vertex V1, V2; //点
cin >> Num_of_Node >> Num_of_Edge; //输入顶点数、边数
Graph G{ Num_of_Node }; //定义图
//输入图
for (int i = 0; i < Num_of_Edge; i++) {
cin >> V1 >> V2; //输入边
G.InsertEdge(V1, V2); //插入边
}
//DFS
G.Init_Visited(); //将标识初始为false
for (int i = 0; i < Num_of_Node; i++) {
if (G.Visited[i] != true) {
cout << "{ ";
G.DFS(i);
cout << "}\n";
}
}
G.Init_Visited(); //将标识初始为false
for (int i = 0; i < Num_of_Node; i++) {
if (G.Visited[i] != true) {
cout << "{ ";
G.BFS(i);
cout << "}\n";
}
}
return 0;
}
Graph::Graph(int VertexNum) {
Nv = VertexNum;
Ne = 0;
Visited = new bool[VertexNum];
for (int i = 0; i < VertexNum; i++) {
for (int j = 0; j < VertexNum; j++) {
G[i][j] = 0;
}
}
}
void Graph::InsertEdge(Vertex V1, Vertex V2) {
//这里可以加判断有没有加过这条边
//插入边 <V1, V2>
G[V1][V2] = 1;
//插入边 <V2, V1>
G[V2][V1] = 1;
Ne++;//边数加1
}
void Graph::DFS(Vertex V) {
cout << V << " "; //输出V
Visited[V] = true; // 标记V已访问,防止出现死循环
for (int i=0; i<Nv; i++) {
if (!Visited[i] && G[V][i]) {
DFS(i);
}
}
}
void Graph::BFS(Vertex V) {
queue<Vertex> Q;
Vertex W;
cout << V << " "; //输出V
Visited[V] = true; // 标记V已访问,防止出现死循环
Q.push(V);
while (!Q.empty()) {
W = Q.front();
Q.pop();
for (int i = 0; i < Nv; i++) {
if (!Visited[i] && G[W][i]) {
cout << i << " "; //输出V
Visited[i] = true; // 标记V已访问,防止出现死循环
Q.push(i);
}
}
}
}
void Graph::Init_Visited() {
for (int i = 0; i < Nv; i++) {
Visited[i] = false;
}
}
运行结果
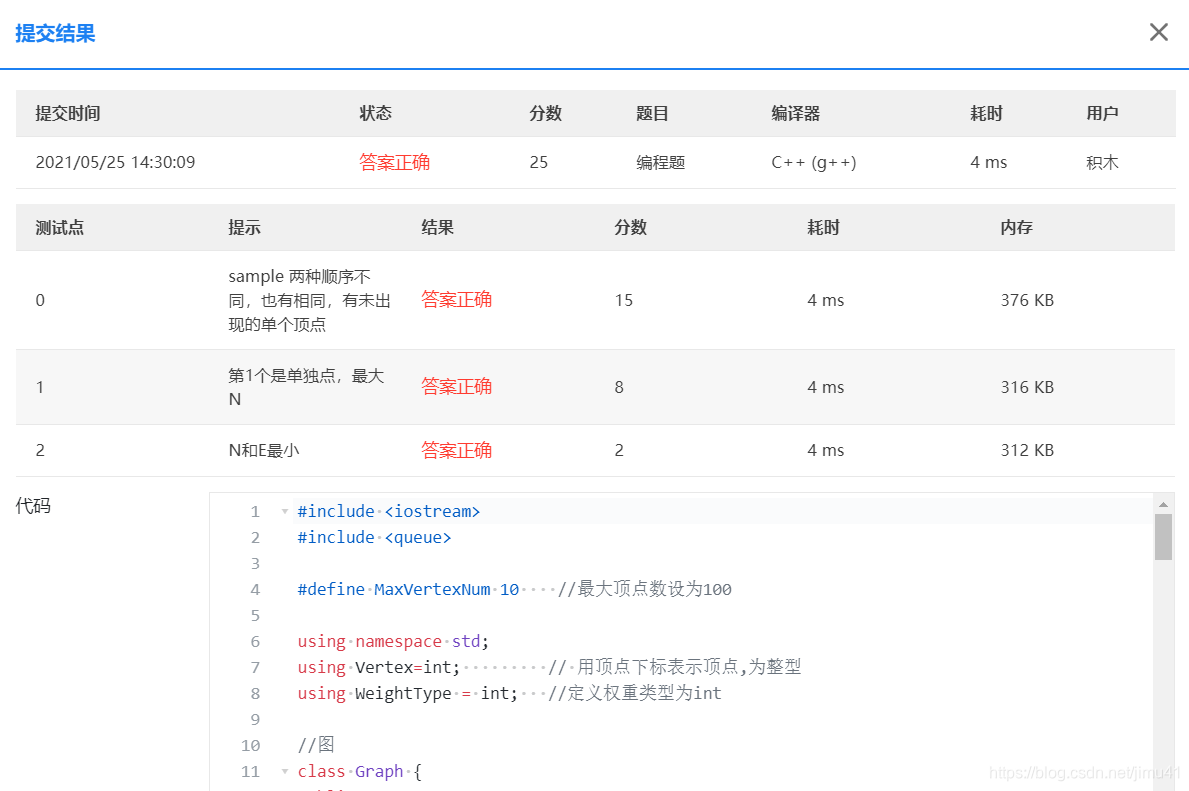





 本文详细讲解了如何利用深度优先搜索(DFS)和广度优先搜索(BFS)算法在给定的无向图中找出所有的连通集。通过实例代码展示了如何在C++中实现,并提供了输入输出样例。
本文详细讲解了如何利用深度优先搜索(DFS)和广度优先搜索(BFS)算法在给定的无向图中找出所有的连通集。通过实例代码展示了如何在C++中实现,并提供了输入输出样例。

















 830
830

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










