【Kakutani conjecture】角谷猜想 · 冰雹猜想

原创

已于 2024-11-14 19:33:58 修改 · 1.7k 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #开发语言 #算法

于 2024-11-14 19:31:46 首次发布

什么是角谷猜想or冰雹猜想？

冰雹猜想 [1]是指：一个正整数x，如果是奇数就乘以3再加1，如果是偶数就析出偶数因数2ⁿ，这样经过若干个次数，最终回到1。 [2]

无论这个过程中的数值如何庞大，就像瀑布一样迅速坠落。而其他的数字即使不是如此，在经过若干次的变换之后也必然会到纯偶数：4-2-1的循环。据日本和美国的数学家攻关研究，在小于7*10^11的所有的正整数，都符合这个规律。 [3]

相关故事

1976年的一天，《华盛顿邮报》于头版头条报道了一条数学新闻。文中记叙了这样一个故事：

70年代中期，美国各所名牌大学校园内，人们都像发疯一般，夜以继日，废寝忘食地玩弄一种数学游戏。这个游戏十分简单：任意写出一个正整数N，并且按照以下的规律进行变换：

如果是个奇数，则下一步变成3N+1。

如果是个偶数，则下一步变成N/2。

不单单是学生，甚至连教师、研究员、教授与学究都纷纷加入 [8]。为什么这种游戏的魅力经久不衰？因为人们发现，无论N是怎样一个数字，最终都无法逃脱回到谷底1。准确地说，是无法逃出落入底部的4-2-1循环，永远也逃不出这样的宿命。

黑洞4-2-1，视界8，主旋臂3*5+1=32/2=16，奇点(4-1)/3=(2+1)/3=1

这就是著名的“冰雹猜想” [9]。

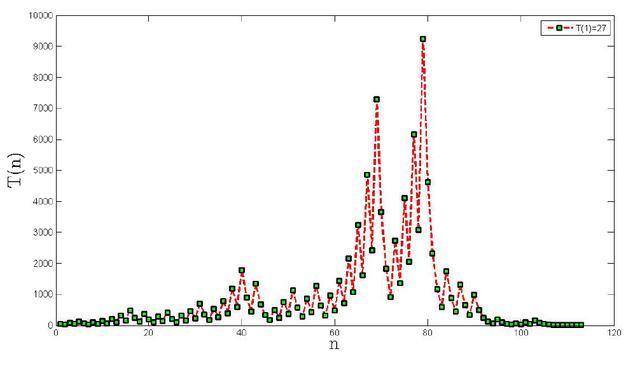
强悍的27

27的归一步数要经过多次剧烈波动的奇偶变换，其路径呈不光滑锯齿

冰雹的最大魅力在于不可预知性。英国剑桥大学教授John Conway找到了一个自然数27。虽然27是一个貌不惊人的自然数，但是如果按照上述方法进行运算，则它的上浮下沉异常剧烈：首先，27要经过77步骤的变换到达顶峰值9232，然后又经过34步骤到达谷底值1。全部的变换过程（称作“雹程”）需要111步，其顶峰值9232，达到了原有数字27的342倍多，如果以瀑布般的直线下落（2的N次方）来比较，则具有同样雹程的数字N要达到2的111次方。其对比何其惊人！

但是在1到100的范围内，像27这样的剧烈波动是没有的（54等27的2的次方倍数的数除外）。

验证规律

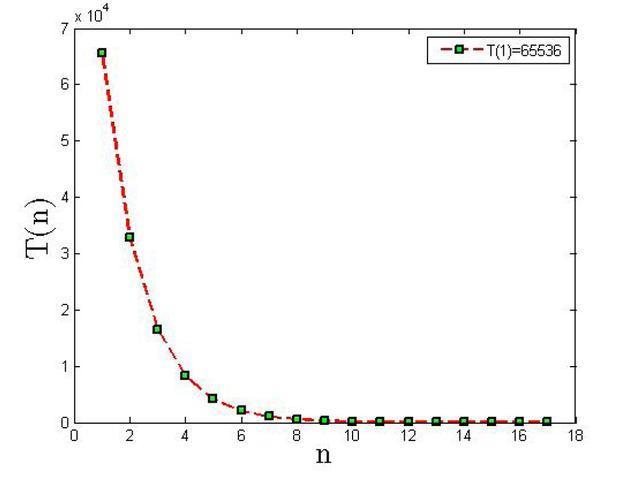
与27形成鲜明对比，2^16是零波动的光滑反比例曲线，呈单调递减

经过游戏的验证规律，人们发现仅仅在兼具4k和3m+1（k,m为自然数）处的数字才能产生冰雹猜想中“树”的分叉。所以在冰雹树中，16处是第一处分叉，然后是64……以后每隔一节，产生出一支新的支流。

自从Conway发现了神奇的27之后，有专家指出，27这个数字必定只能由54变来，54又必然从108变来，所以，27之上，肯定可以出现不亚于2^n的强大支流——3^3*2^n(n=1，2，3……)，然而，27到4-2-1数列和本流2到4-2-1数列要遥远的多。按照机械唯物论的观点，从27开始逆流而上的数列群才能叫做本源，尽管如此，按照“直线下泻”的观点，一般依然把1-2-4-8……2n的这一支看作是“干流”。

又称角谷猜想，因为是一个名叫角谷的日本人把它传到中国。

数列验证法，此方法是根据冰雹猜想的验证规则而建立的一种验证方法，是以无限的数列来对付无限的自然数。首项偶数，公差是偶数，那么数列上的所有自然数都是偶数，全体数列除于2，如果首项是奇数公差是偶数，那么数列上全体自然数都是奇数，全体乘上3再加1。如果公差是奇数，首项也是奇数，那么第奇数项必定都是奇数则乘上3再加1，第偶数项必定都是偶数,则除于2。如果公差是奇数，首项是偶数，那么第奇数项必定都是偶数，则除于2，第偶数项必定都是奇数，则乘上3再加1。按照这样的计算规则计算下去，会遇到许多新的问题，考验验证者的智商。比如偶数的通项公式是2n，因为都是偶数所以除于2，得到n，这就是自然数。

按照忽略偶数不记录的验证方法进行验证，第一个被验证的奇数有可能是能被3整除的奇数，也有可能是不能被3整除的奇数。但是，3x+1以后，所到达所归结的第二个奇数，以及第三个奇数（假设存在）...整个过程所到达所遇到所归结所访问到的每一个奇数，必定都不能再被3整除了。如果都从从能被3整除的奇数开始验证，路径上所遇到所归结的所到达所访问到的每一个奇数都必定不能再被3整除了，最终都能归结于1，那么必定遍历所有的奇数（遍历是离散数学的概念）。如果都从不能被3整除的奇数开始验证，那么路径上所遇到所到达所归结的所访问到的每一个奇数必定都不可能再被3整除了，最终都归结于1（等于说是漏下能被3整除的奇数没有被验证）。所以在顺向的冰雹猜想验证过程中，可以把能被3整除的奇数都命名为最起始点的奇数，1是终止点的奇数，而在逆向的冰雹猜想验证过程中则是相反的，1是最起始点的奇数，而能被3整除的奇数则是终止点的奇数。事实上在验证的过程中，不能被3整除的奇数，都在存在数量无穷多的上一步的奇数，占1/3的比例是能被3整除的奇数，占2/3的比例是不能被3整除的奇数，这一现象都跟自然数的情况出奇地巧合了 [10].这一规律，无论是单个奇数的验证方法，还是等差数列验证法必须遵守。在能被3整除的奇数之前的，只有能被3整除的偶数，没有任何奇数。

这种新的验证方法存在缺陷，就是运算不连续，虽然也可以用于验证爬升或者下降...爬升的时候需要对2进行因式分解......下降的时候需要先把3^n给计算出来....所以比较麻烦.....优点只有一个，那就是当验证到近乎无限爬升的时候....比如说(2n-1)*2^(10^8)-1的验证过程就是把一亿个2换成一亿个3，(2n-1)*3^(10^8)-1，一次性替换，我们需要把3^(10^8) 给计算出来，如果按照传统的验证方法，你需要把(2n-1)*2^(10^8)-1给算出来，然后再爬升(10^-1)步以后才能得到这个结果

把奇数分成2类：

能被3整除的奇数：通项公式是6(n-1)+3 这一类的奇数是不可以通过3x+1得到的又叫最起始点的奇数这一类的奇数不可能发生病态归结的，因为从这一类奇数开始计算可以得到其他奇数，而从其他奇数开始计算绝对不能得到这一类的奇数。

再看看7x+1 ,15x+1 ,7x-3 ,15x-7,他们的最起始点的奇数就不只是能被7整除那么简单了..........

不能被3整除的奇数：通项公式分别是：6（n-1）+1 和6(n-1)+5...他们都是可以通过3x+1得到的，又叫路径上的奇数或者是过程奇数，有可能是主病态归结点的奇数就属于这两类。

存在X1，使得X1*3+1之后只能被1个2整除，之后就是奇数，这一类奇数占奇数总量的1/2；

存在X2，使得X2*3+1之后只能被2个2整除，之后就是奇数，这一类奇数占奇数总量的1/4；

存在X3，使得X3*3+1之后只能被3个2整除，之后就是奇数，这一类奇数占奇数总量的1/8。

函数f(n)通过奇偶迭代织成蜘蛛网，射线为3n+1,螺旋线为(3n+1)/2

公式列于此

Xs+₁=(3Xs+1)/2ⁿ

基于克拉茨问题推广

角谷猜想又叫叙古拉猜想。它的一个推广是克拉茨问题，下面简要说说这个问题：

50年代开始,在国际数学界广泛流行着这样一个奇怪有趣的数学问题:任意给定一个正整数x,如果是偶数,则变换成x/2,如果是奇数,则变换成3x+1.此后,再对得数继续进行上述变换.例如x=52,可以陆续得出26,13,40,20,10,5,16,8,4,2,1.如果再做下去就得到循环:

(4,2,1).再试其他的正整数也会得出相同的结果.这个叫做叙古拉猜想.

上述变换,实际上是进行下列函数的迭代

{ x/2 (x是偶数)

C(x)=

3x+1 (x是奇数)

问题是,从任意一个正整数开始,经过有限次函数C迭代,能否最终得到循环(4,2,1),或者等价地说,最终得到1?据说克拉茨(L.Collatz)在1950年召开的一次国际数学家大会上谈起过,因而许多人称之为克拉茨问题.但是后来也有许多人独立地发现过同一个问题,所以,从此以后也许为了避免引起问题的归属争议,许多文献称之为3x+1问题.

悬赏征解

克拉茨问题吸引人之处在于C迭代过程中一旦出现2的幂,问题就解决了,而2的幂有无穷多个,人们认为只要迭代过程持续足够长,必定会碰到一个2的幂使问题以肯定形式得到解决 [12

最低0.47元/天解锁文章