文章首先介绍了2-3-4 树的原理,这是理解红黑树的关键,再介绍了红黑树的原理。理解之后,不必再死记硬背任何知识点,可以随时写出一棵红黑树。
前言
学习的真谛是记忆、但绝对不是死记硬背。理解之后的记忆会更加深刻、更难遗忘,就算忘记,也能很快的捡起来。本文将带你搞明白红黑树的原理。看到这篇文章的小伙伴,耐下心来,跟博主一起认真学习吧。
记得第一次看到 “红黑树” 这个概念。首先让我想到的是,现实中树木是有颜色的。但在我们的数据结构中,树为什么会有颜色呢?颜色又为什么是红色呢?可以是绿色或者其他颜色么?
1978年罗伯特·塞奇威克(Robert Sedgewick)在论文《A dichromatic framework for balanced trees》第一次提出了红黑树的概念,表示红色代表的该节点的 "balance information"。至于为什么用红色,据说因为当时作者在一家生产打印机的公司做访问学者,发现打印机工作时所发出的红色光芒非常漂亮,作者很喜欢。因此用红色代表了该数据结构里的“balance information”,因此数据结构的树也就了颜色。
首先我们首先看一下2-3-4树的概念和原理,这个是我们理解红黑树原理的关键
一、2-3-4 树
1.1 、概念
任一节点只能是2节点、3节点或4节点,并保持"Perfect balance"的排序树。示例如下(注意图片中的红色字体,体现了排序的概念) :
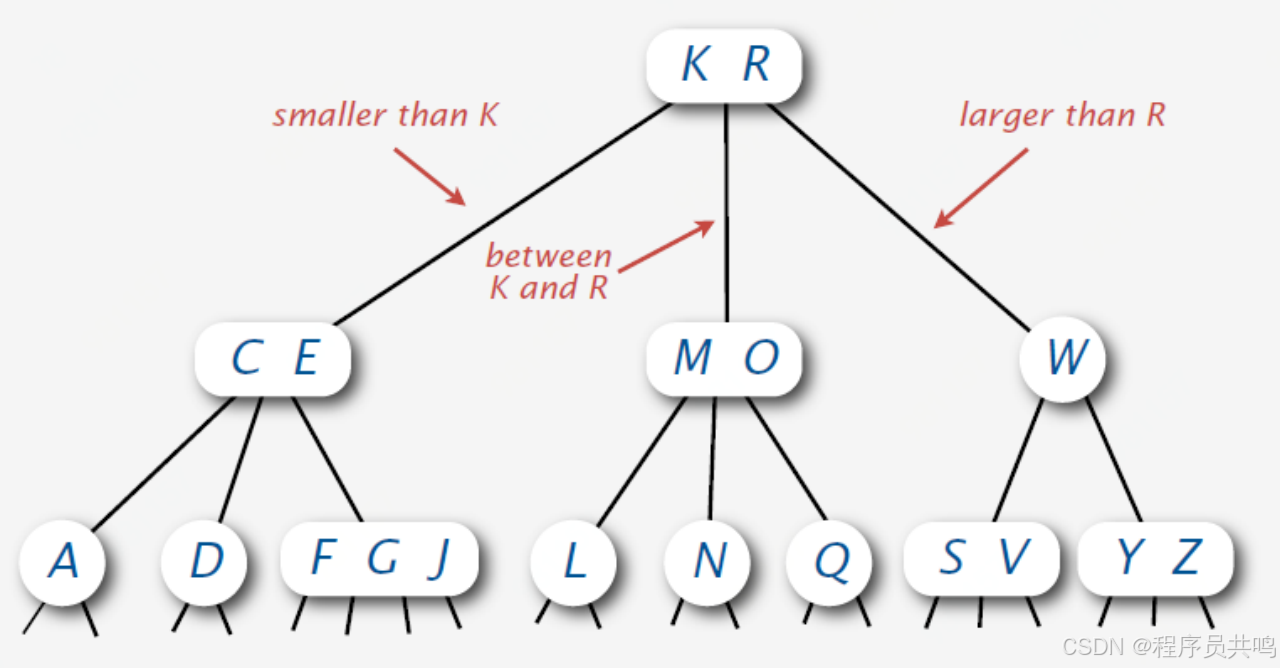
概念包括三部分。“2节点、3节点、4节点”、"Perfect balance"和 排序树。分别介绍下三个点。
(1)2节点、3节点、4节点
2节点:1个关键字,2个子节点或者无子节点 ,如上图中的 A 节点 和 W节点;
3节点:2个关键字,3个子节点或者无子节点,如上图中的“ C 、E” 节点 和 "S、V" 节点;
4节点:3个关键字,4个子节点或者无子节点,如上图中的 "F、G、J" 节点;
(2) Perfect balance
论文中的定义是:Perfect balance:Every path from root to leaf has same length。
每一条从根节点到叶子节点路径的长度都有相同。
(3) 排序树
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
结合概念,查找某个节点 查找“L”。
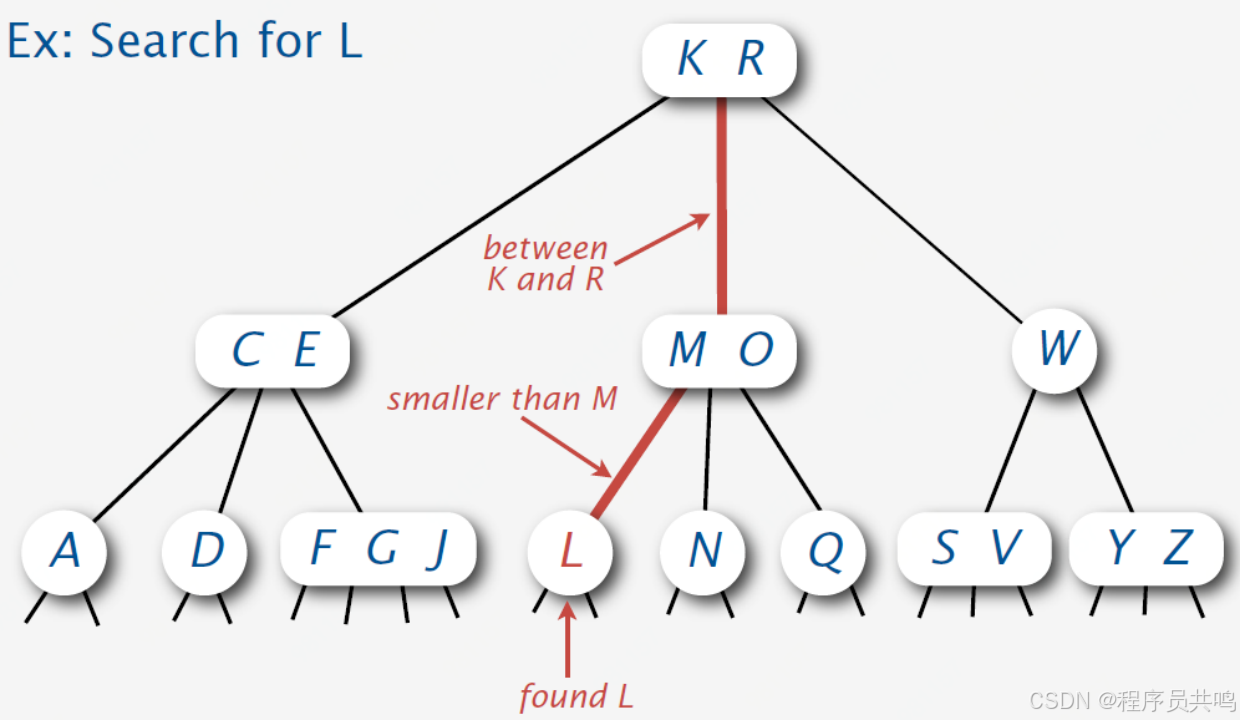
1.2 、构建一棵2-3-4树
1.2.1 插入不同的叶子结点
(1)当前节点是2节点
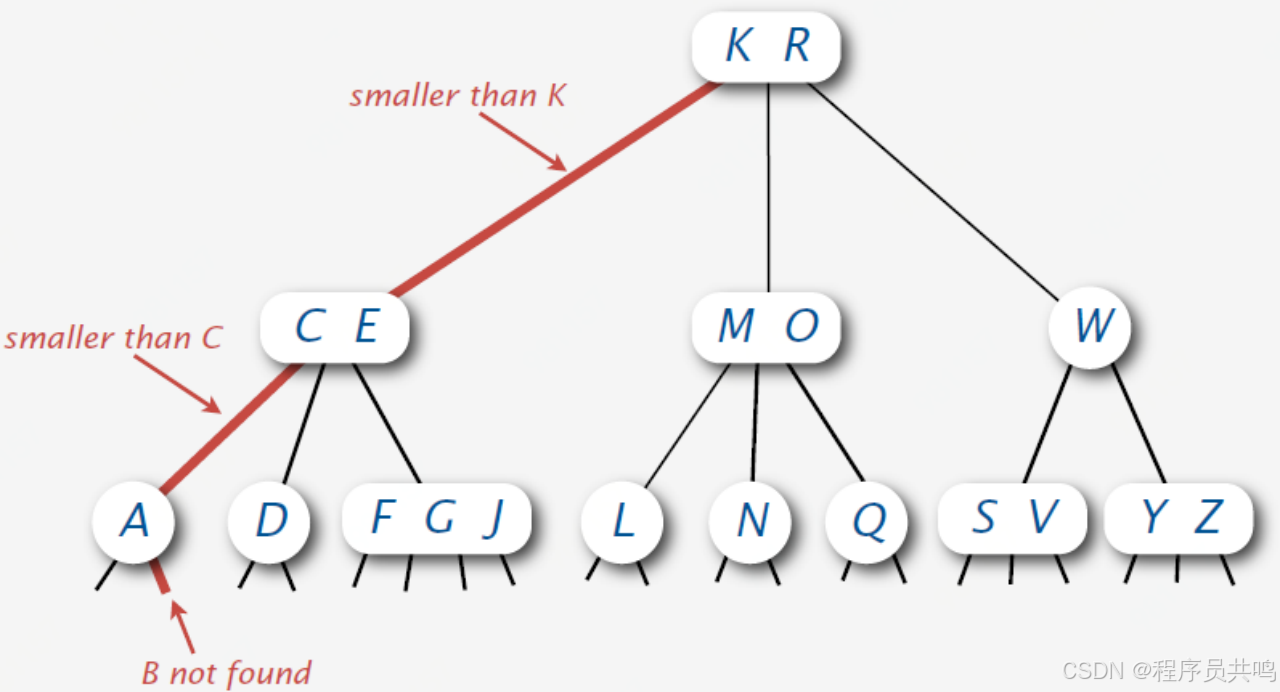
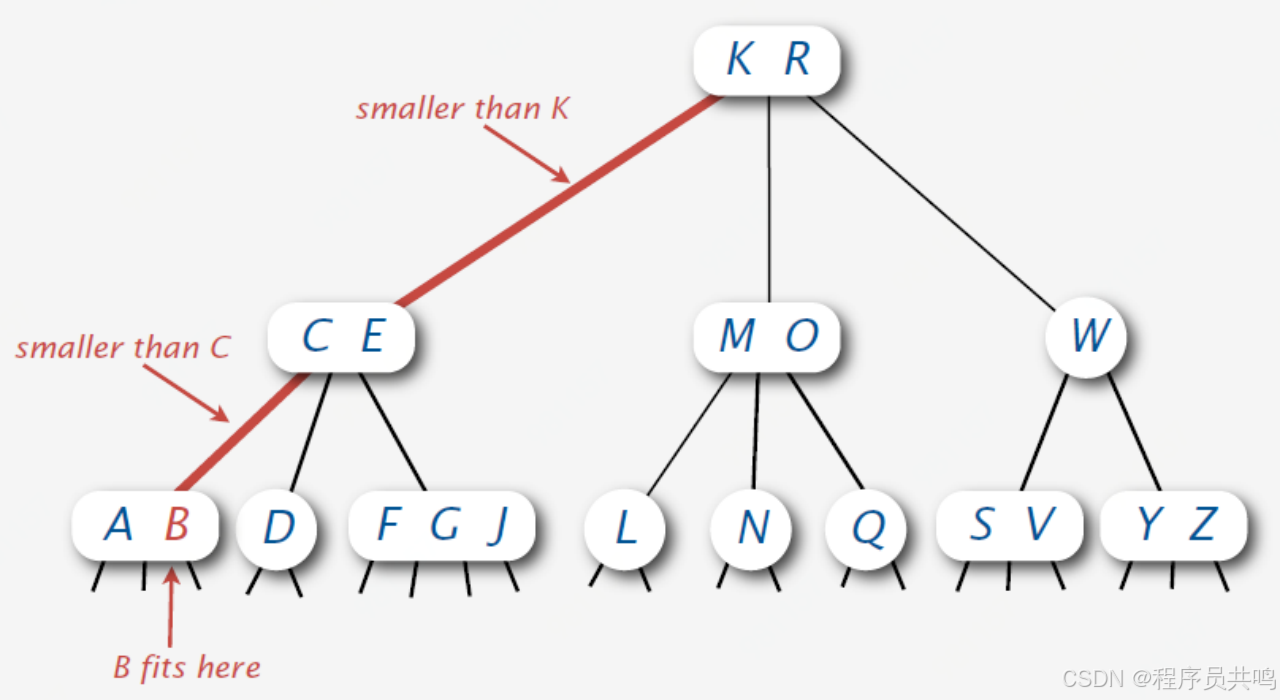
(2)当前节点是3节点
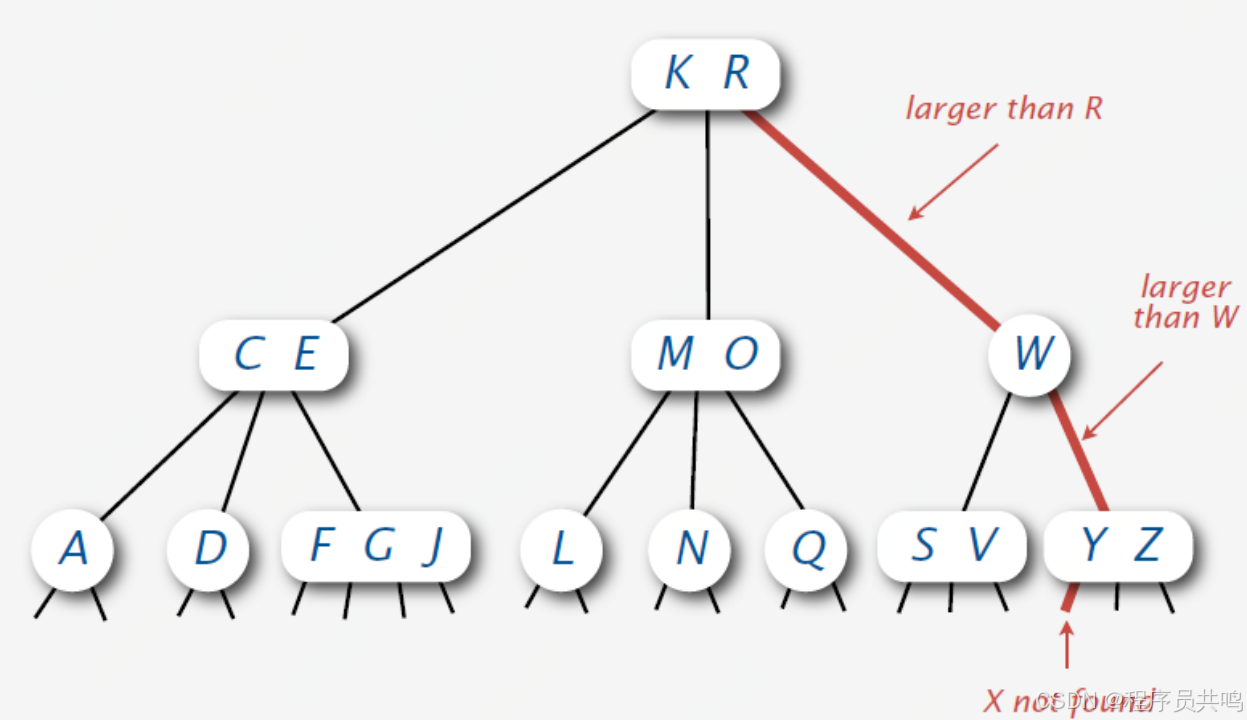
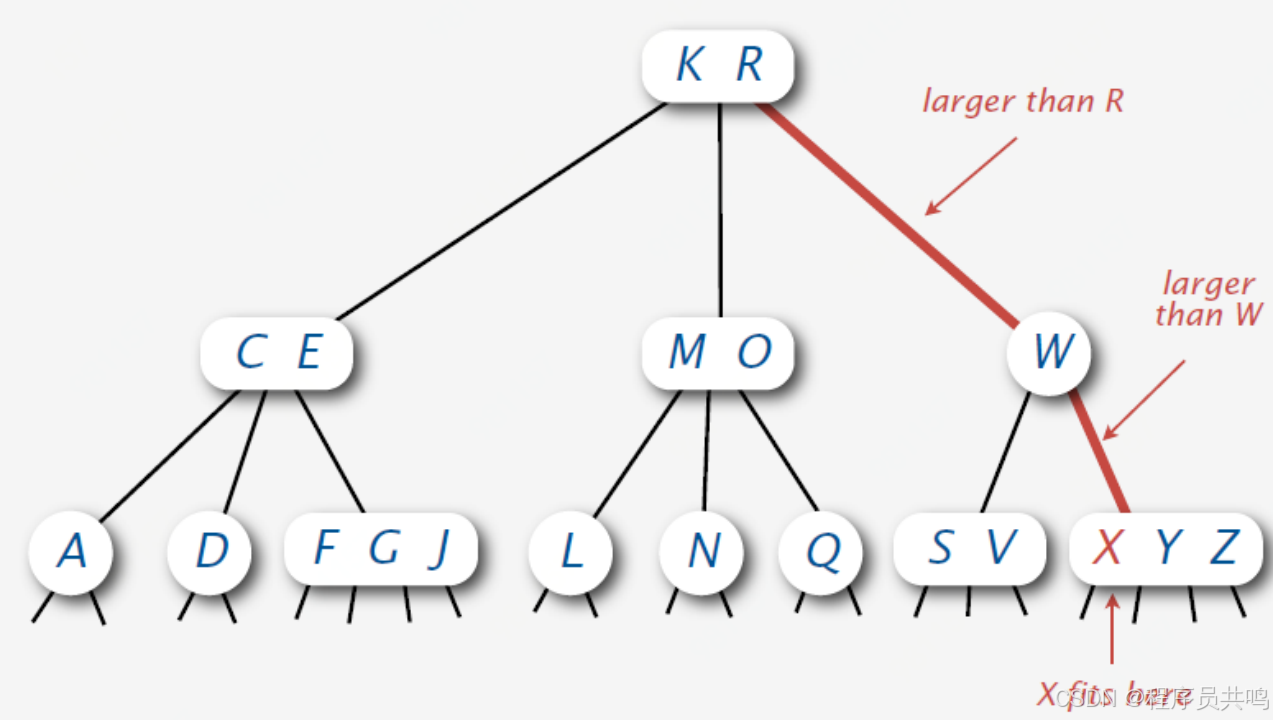
(3)当前节点是4节点
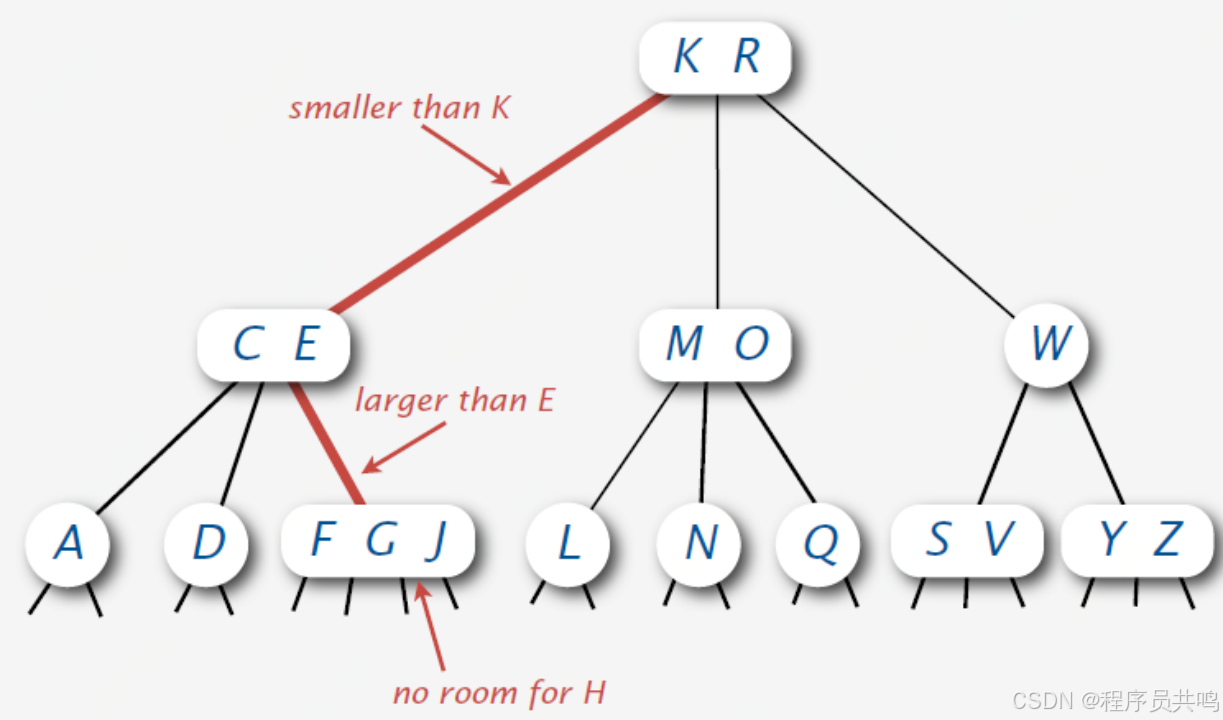
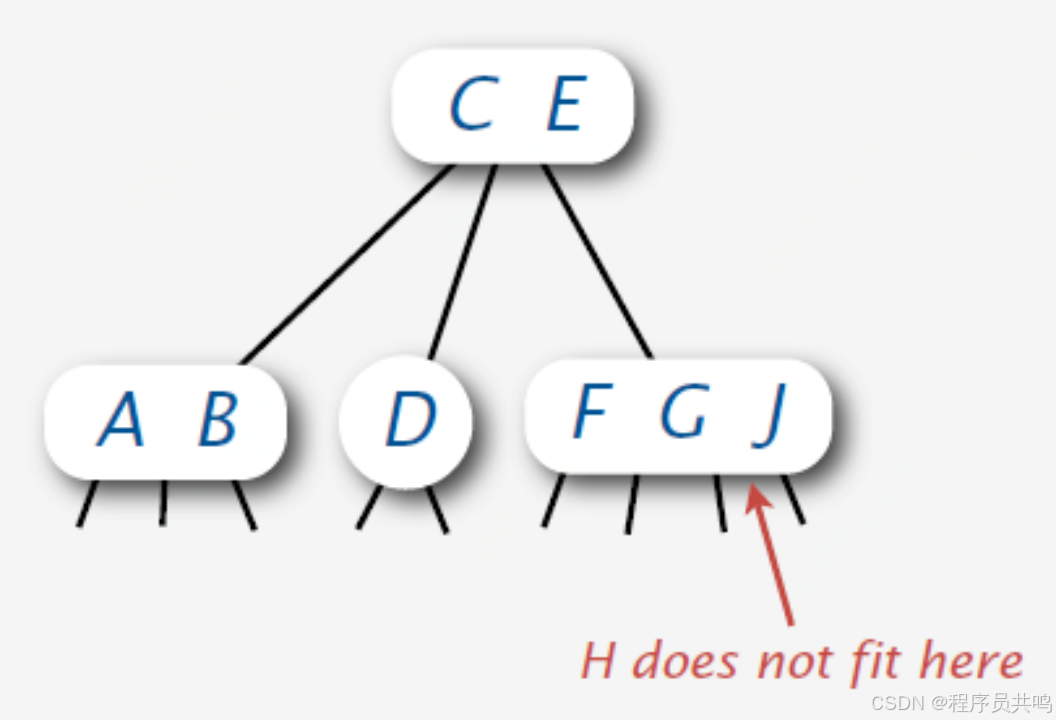
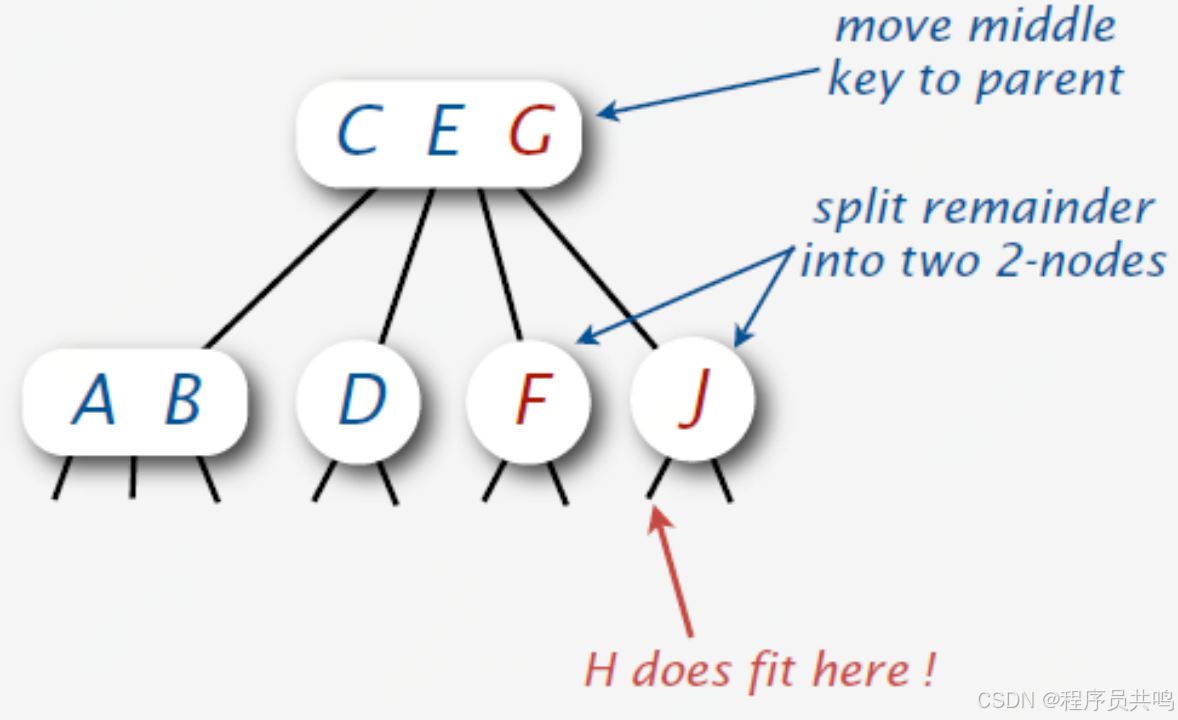
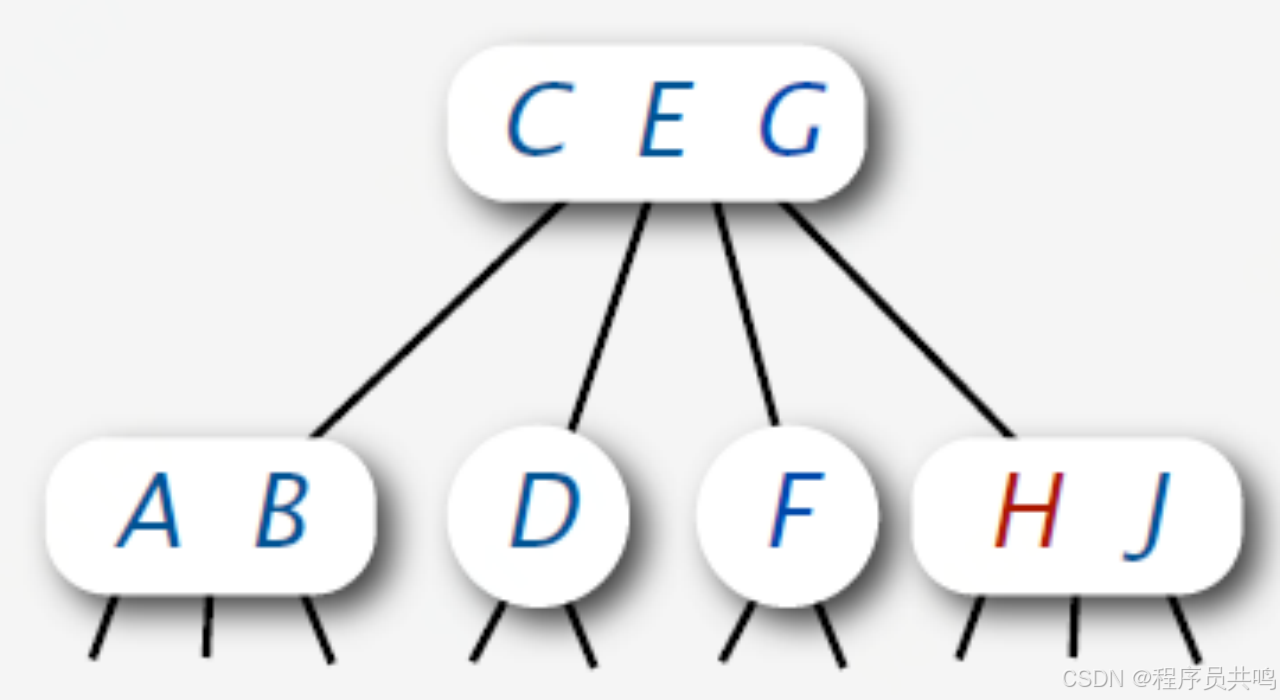
问题:如果父节点是4节点怎么办? 如下,插入M
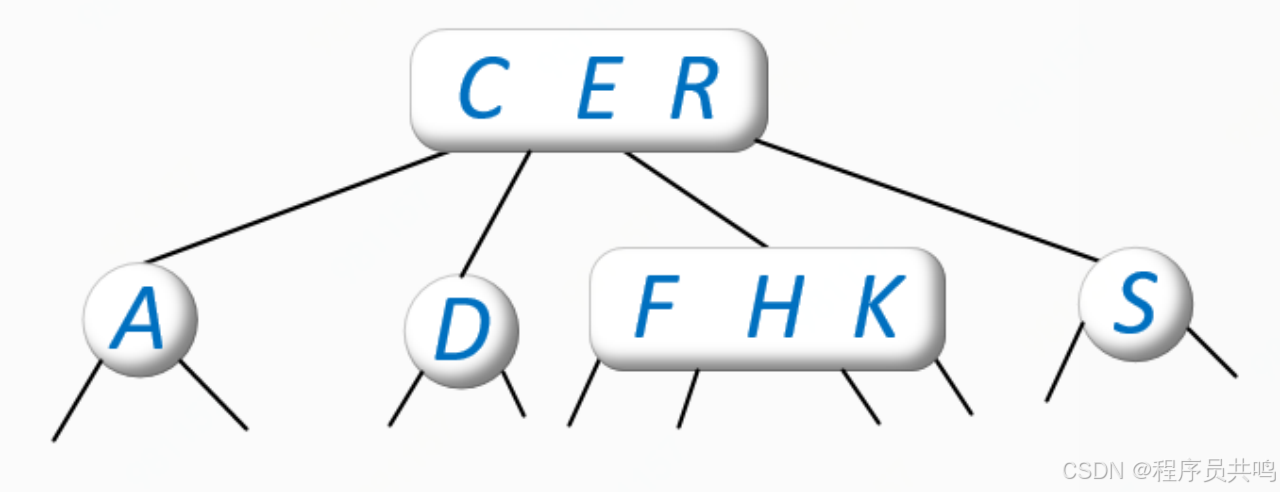
1.2.2 构建2-3-4树的两种方法
(1) 自下而上的构建方法
插入4节点,中间关键字移动到父节点中,如果是4节点,那么祖父节点中间关键字,继续往上移动,依次类推。插入顺序:A、S、E、R、C、D、I、N、B、X 、F、M
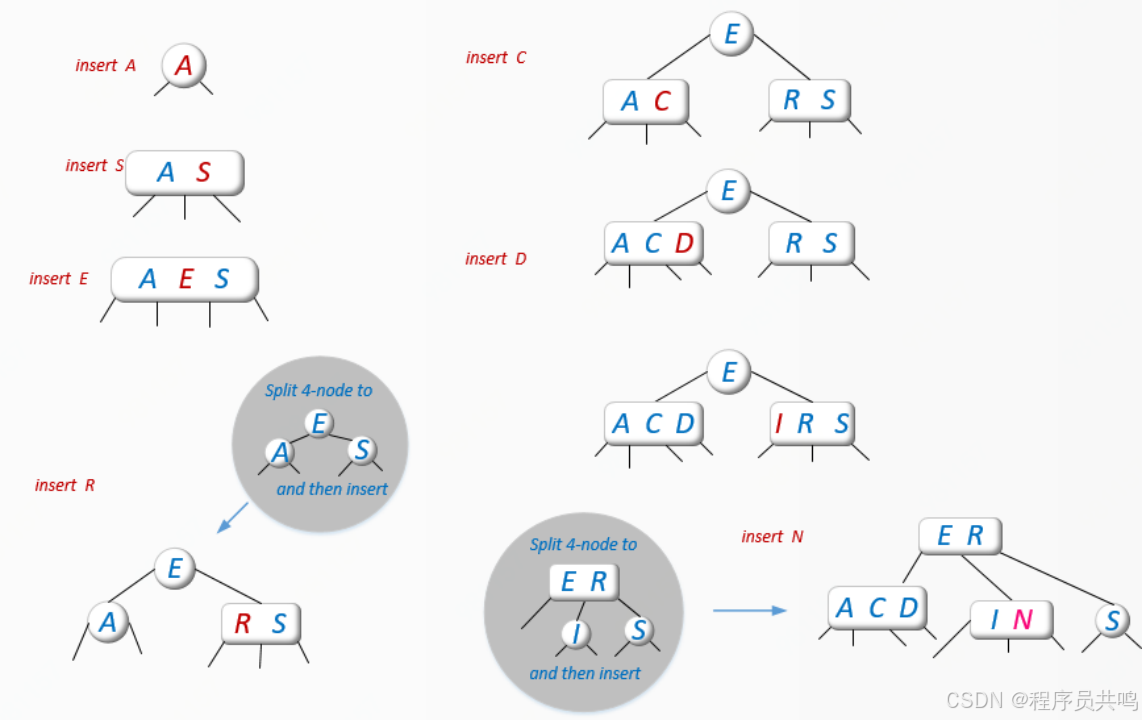
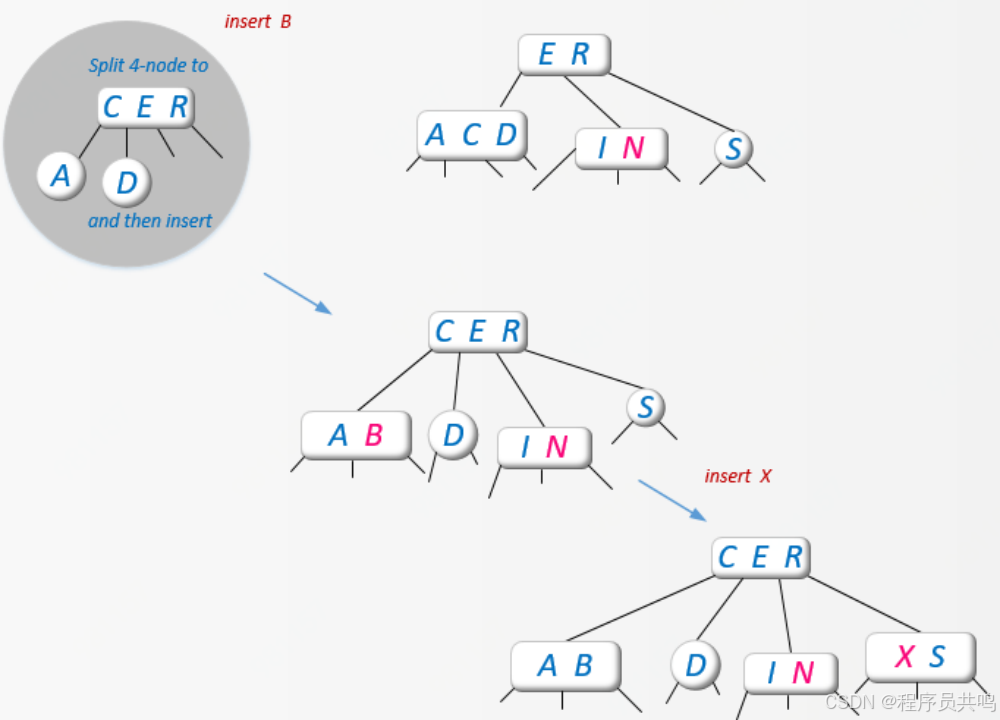
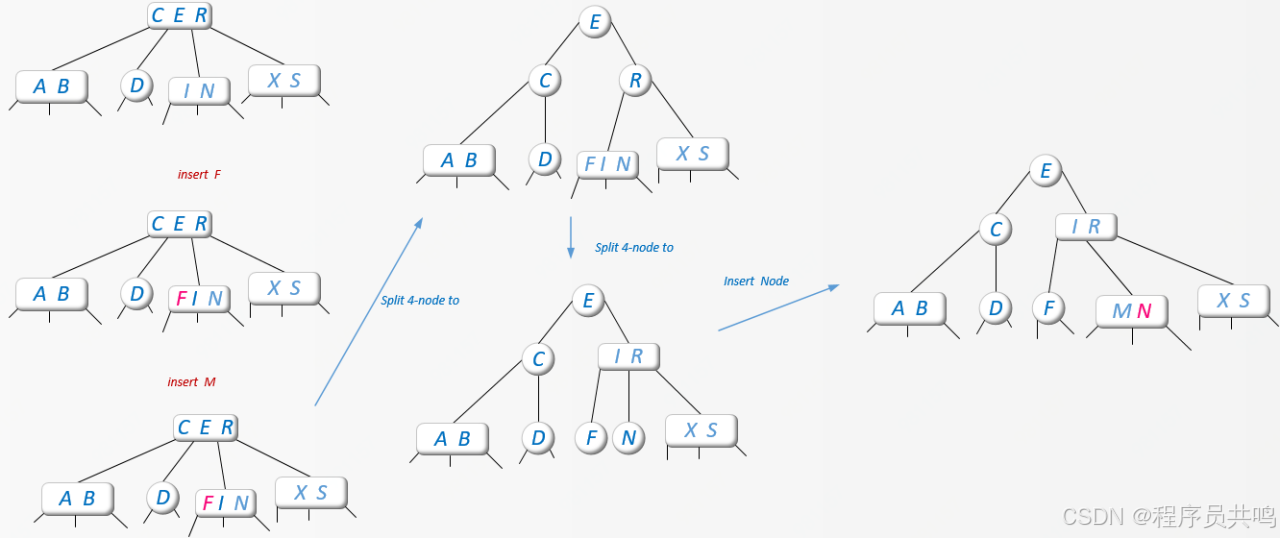
(2)自上而下的构建方法
原则:“当前节”点不是4节点。 寻找的过程,如果当前节点是4节点,则把中间节点往上升,则要加入的节点永远是2节点或者3节点。
插入顺序:A、S、E、R、C、D、I、N、B、X
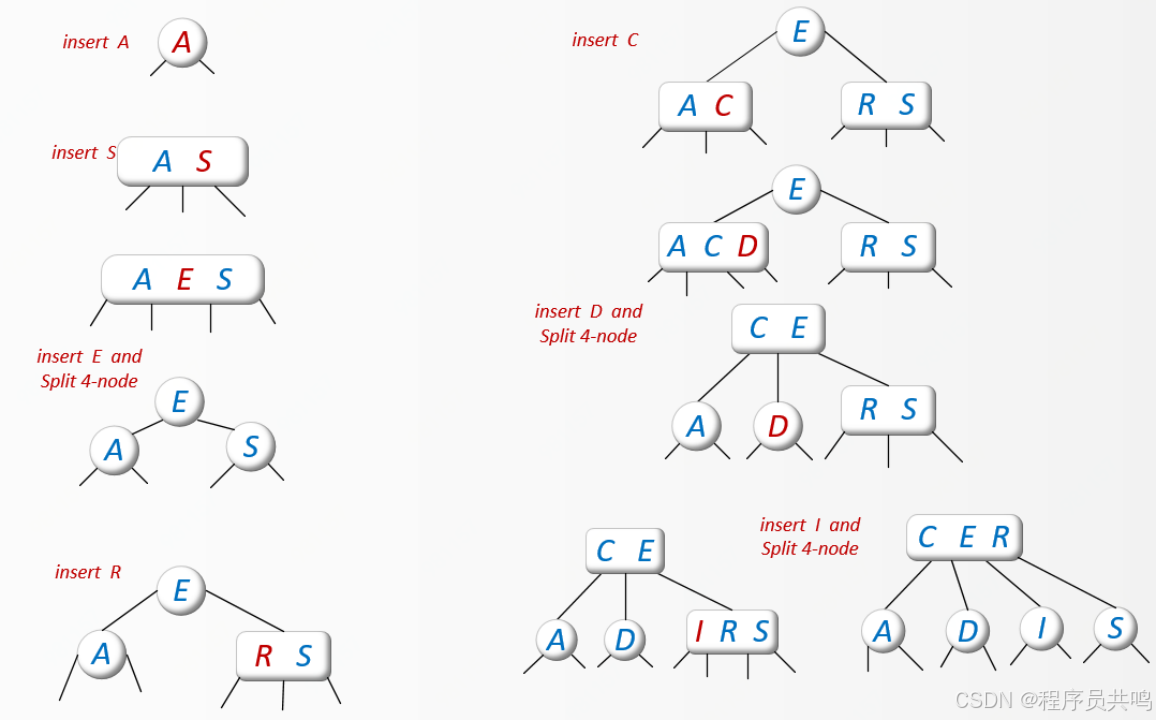
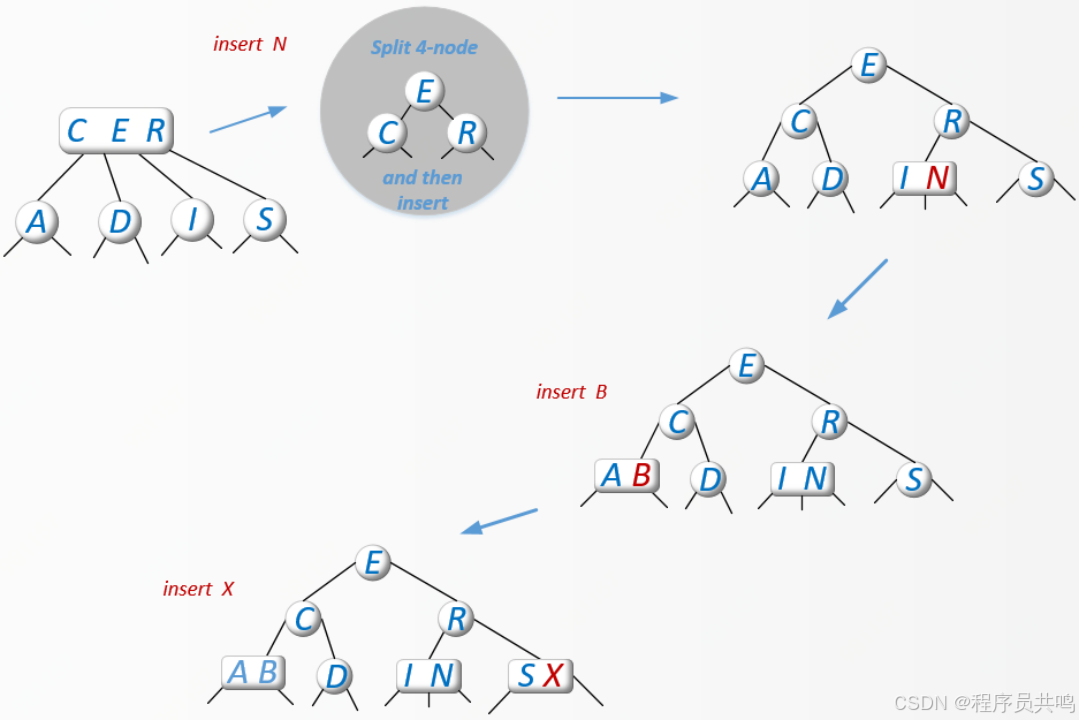
(3)练习
根据下列给定关键字,采用“自下而上”方法构建红黑树。
![]()
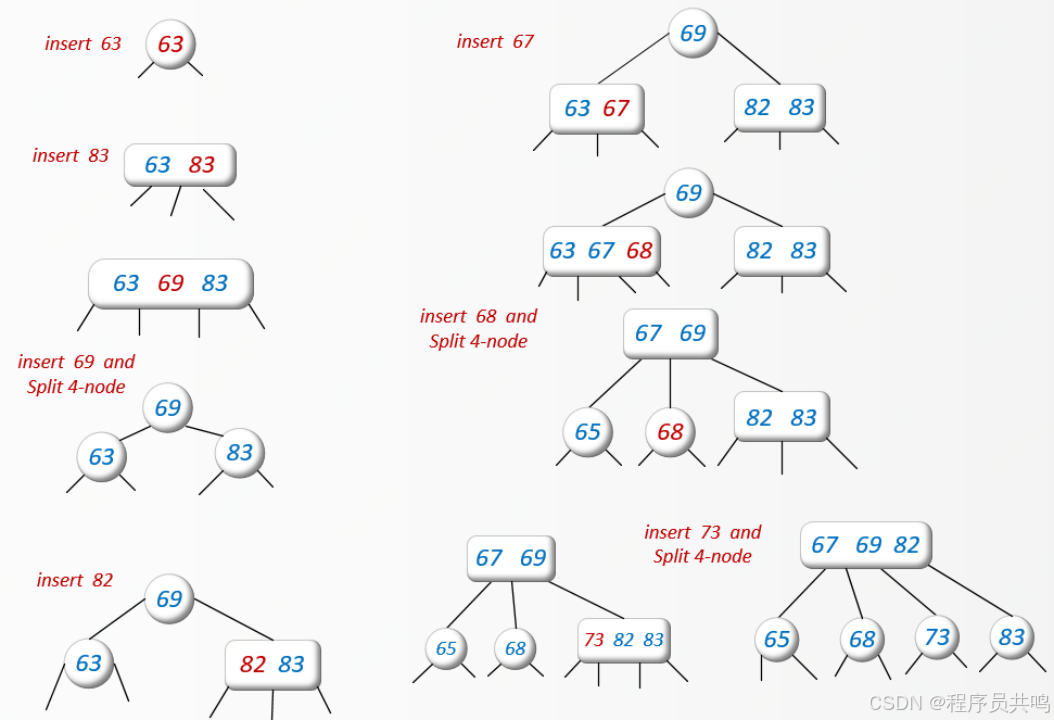
二、红黑树
2.1 概念
红黑树是一种特殊的二叉搜索树,必须满足以下几个特性:
1. 每个节点或是黑色或是红色;
2. 根节点是黑色;
3. 每个叶节点是黑色(叶节点为空节点);
4. 如果一个节点是红色,则它的子节点必须是黑色;
5. 从一个节点到该节点的所有叶节点的路径包含相同数目的黑色节点。
2.2 红黑树和2-3-4树的概念
(1)红黑树和2-3-4 树的关系 红黑树( Red-black trees ,Guibas-Sedgewick, 1978)
a. 把2-3-4树 看做 二叉搜索树
b. 用红链接表示3节点和4节点
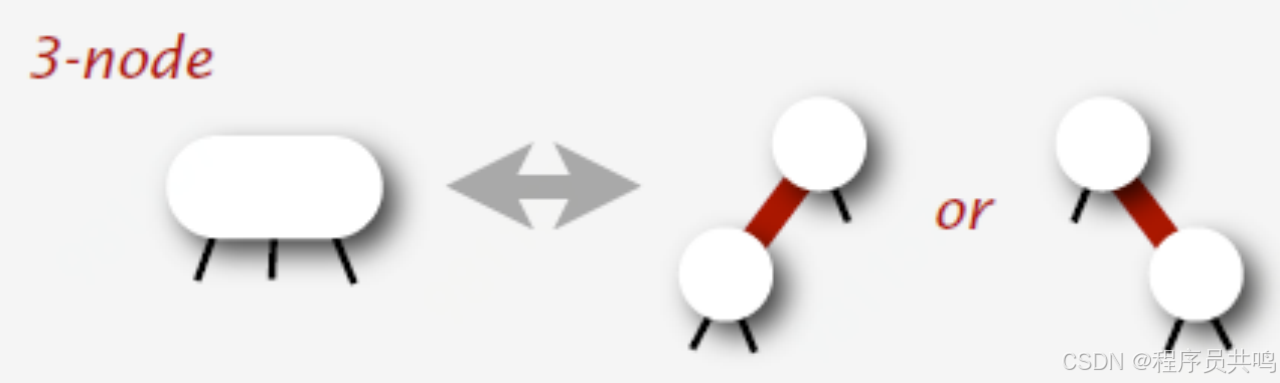

(2) 左倾红黑树 ( Left-leaning red-black trees ,Sedgewick, 2008 )
a.把2-3-4树 看做 二叉搜索树
b.用红链接表示3节点和4节点
c.3节点必须向左倾斜


2.2 红黑的三种操作
(1)左旋。红色连接向左旋转
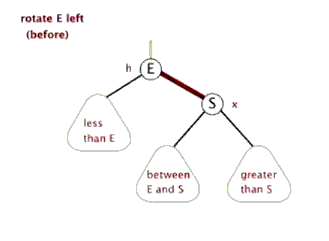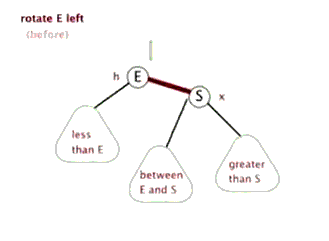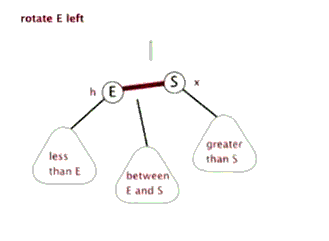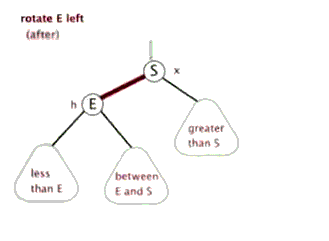
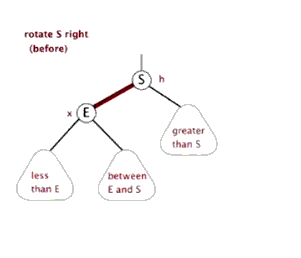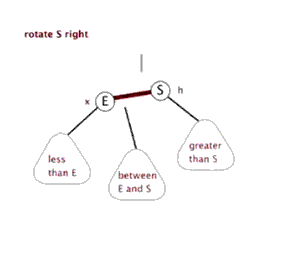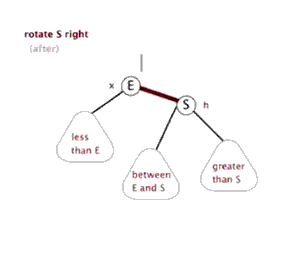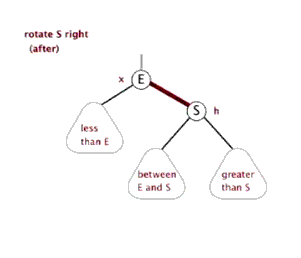
(2)右旋。红色连接向右旋转。
(3) 变色
2.4 原理
构建红黑树原理——将红黑树看做2-3-4树。
(1)父节点是一个 2节点
当前4节点为父节点的左子节点

当前4节点为父节点的右子节点

(2)父节点是一个 3节点
左分支

中间分支

右分支

(3)到达叶子节点为2节点
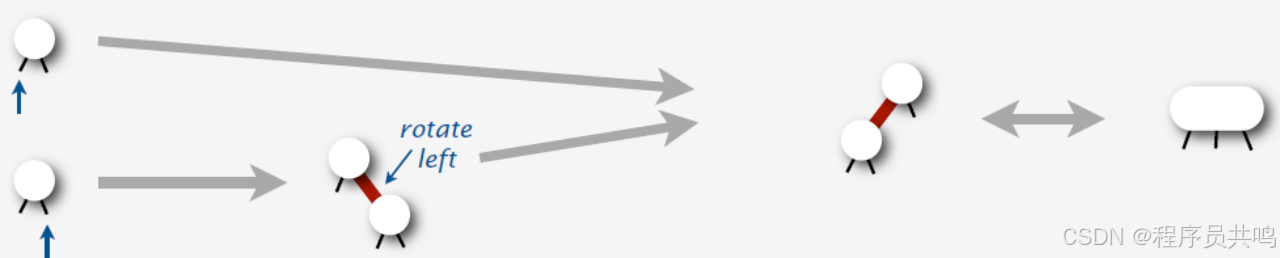
(4)到达叶子节点为3节点
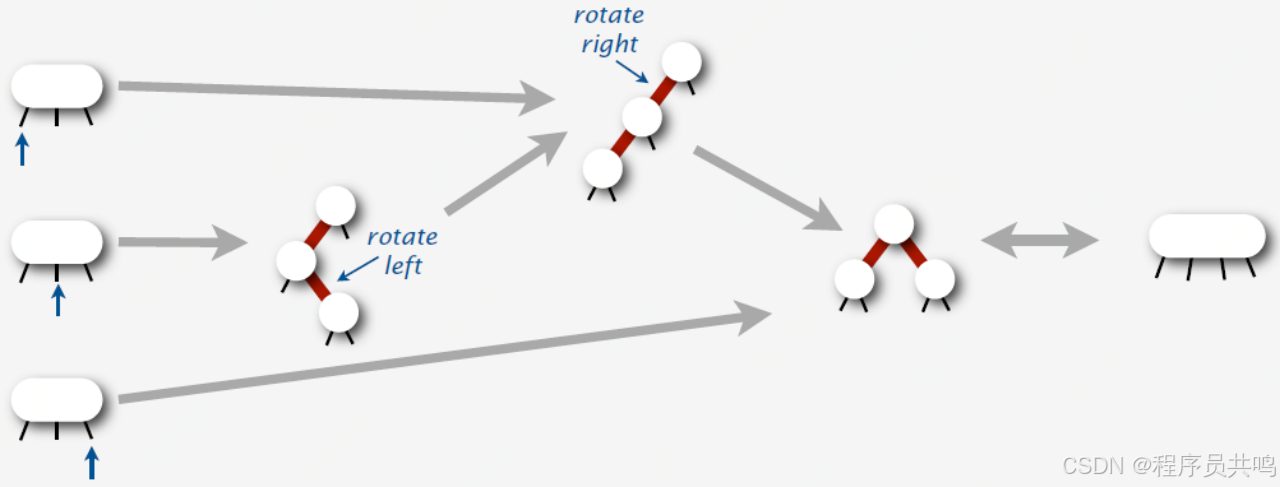
(5)红黑树构建代码

三、红黑树性能分析
3.1 二叉搜索树-平均搜索性能
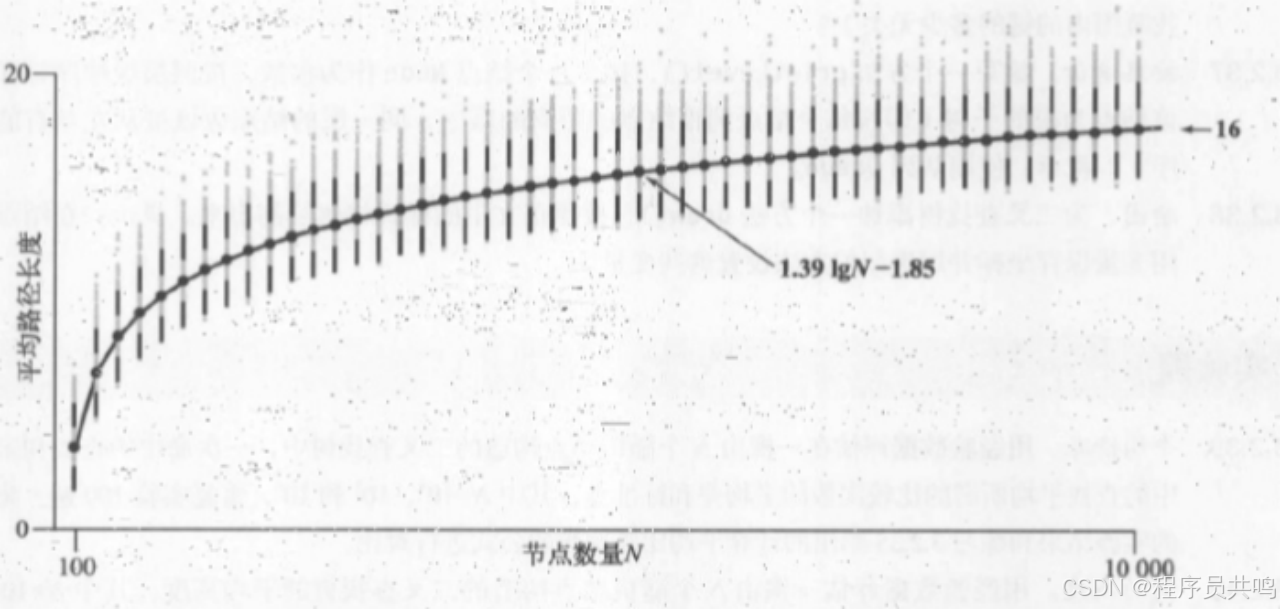
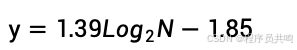
3.2 红黑树
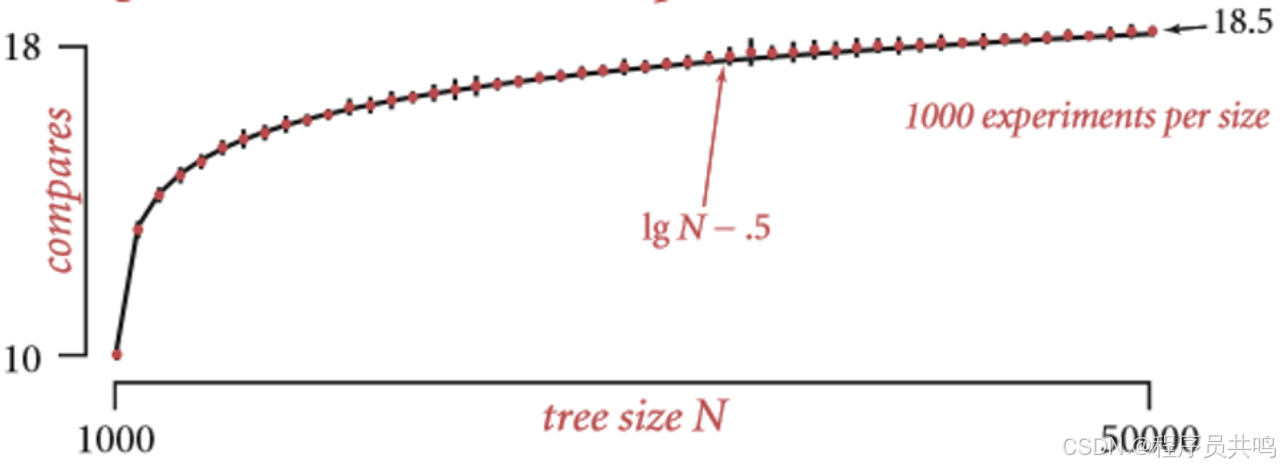
![]()




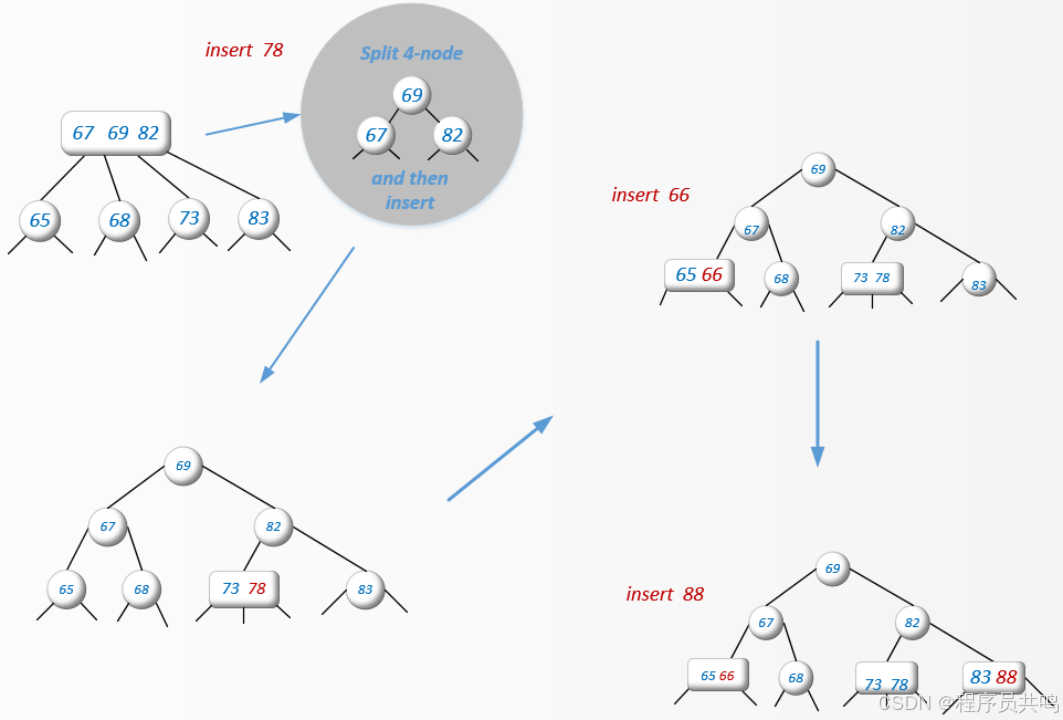




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








