时间限制:10000ms
单点时限:1000ms
内存限制:256MB
-
0 7 2 0 5 0 0 3 0
样例输出 -
6 7 2 1 5 9
8 3 4
-
DFS
-
package hiho; import java.util.Scanner; public class Main { private static final int MAX = 10; private static int[] graph = new int[MAX]; private static int[] vis = new int[MAX]; private static int[] ans = new int[MAX]; private static int flag = 0; public static void main(String[] args) { // TODO Auto-generated method stub Scanner scan = new Scanner(System.in); for (int i = 1; i <= 9; i++) { int n = scan.nextInt(); graph[i] = n; vis[graph[i]] = 1; } dfs(1); String str = ""; if (flag==1) { for (int i = 1; i <= 9; i++) { str += ans[i] + " "; if (i % 3 == 0) { System.out.println(str.trim()); str = ""; } } }else{ System.out.println("Too Many"); } } public static void dfs(int pos){ if(pos==10&&isOk()){ flag++; if(flag==1){ for(int i=1;i<=9;i++){ ans[i] = graph[i]; } } return; }else if(pos<10){ if(graph[pos]!=0){ dfs(pos+1); }else{ for(int i=1;i<=9;i++){ if(vis[i]!=0){ continue; } vis[i] = 1; graph[pos] = i; dfs(pos+1); vis[i] = 0; graph[pos] = 0; } } } } public static boolean isOk() { int sum1 = graph[1] + graph[2] + graph[3]; int sum2 = graph[4] + graph[5] + graph[6]; int sum3 = graph[7] + graph[8] + graph[9]; int sum4 = graph[1] + graph[4] + graph[7]; int sum5 = graph[2] + graph[5] + graph[8]; int sum6 = graph[3] + graph[6] + graph[9]; int sum7 = graph[1] + graph[5] + graph[9]; int sum8 = graph[3] + graph[5] + graph[7]; return (sum1 == sum2 && sum2 == sum3 && sum3 == sum4 && sum4 == sum5 && sum5 == sum6 && sum6 == sum7 && sum7 == sum8); } }
描述
小Hi最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。
三阶幻方又被称作九宫格,在小学奥数里有一句非常有名的口诀:“二四为肩,六八为足,左三右七,戴九履一,五居其中”,通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
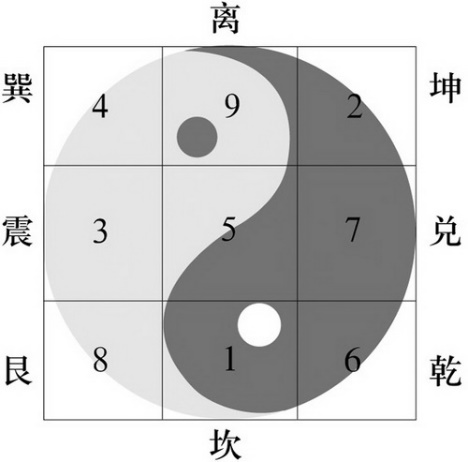
有意思的是,所有的三阶幻方,都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小Hi准备将一个三阶幻方(不一定是上图中的那个)中的一些数组抹掉,交给邻居家的小朋友来进行还原,并且希望她能够判断出究竟是不是只有一组解。
而你呢,也被小Hi交付了同样的任务,但是不同的是,你需要写一个程序~
输入
输入仅包含单组测试数据。
每组测试数据为一个3*3的矩阵,其中为0的部分表示被小Hi抹去的部分。
对于100%的数据,满足给出的矩阵至少能还原出一组可行的三阶幻方。
输出
如果仅能还原出一组可行的三阶幻方,则将其输出,否则输出“Too Many”(不包含引号)。





 本文介绍了三阶幻方的概念,以及如何通过口诀构造九宫格。小Hi抹去了三阶幻方的部分数字,要求判断是否只有一种还原方式。程序需要接收一个3x3矩阵,其中0表示未知数字,输出唯一解或提示存在多种解。
本文介绍了三阶幻方的概念,以及如何通过口诀构造九宫格。小Hi抹去了三阶幻方的部分数字,要求判断是否只有一种还原方式。程序需要接收一个3x3矩阵,其中0表示未知数字,输出唯一解或提示存在多种解。
















 1541
1541

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








