PCA理解

数据降维：减少维度的基础上尽可能保留更多的信息量。也就是说去掉的一些特征对整体影响很小或是特征之间有交叉。

矩阵相乘：物理解释，右边矩阵的每一个列向量变换到左边矩阵每一个行向量的为基的空间中去。

基的数量少于向量本身的维数，可以达到降维效果。->关键在于如何选择基。
二维->一维：保留更多信息->映射到基的点分散->投影后的方差尽可能越大。
三维->二维：保留更多信息->方向1：找到一个方向使得投影后方差最大。方向2：两个字段完全独立->选择第二个基与第一个基正交的方向上选择->协方差为0。

最终优化目标：
将N维向量将为K维，目标：选择K个单位正交基，使得原始数据变换到这组基后，各字段两两协方差为0；而字段方差尽可能大。取K个方差。

算法：
设有m条n维数据。

1）将原始数据按列组成n行m列矩阵X。（m：样本数，n：特征维度，列向量）

2）将X的每一行（不同样本的同一种特征）进行零均值化，减去每行均值。

3）求出协方差矩阵：

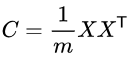
4）求出协方差矩阵的特征值及对应的特征向量。

5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P。

6）Y=PX即为降维到k维后的数据。

本文转于整理于