258. Add Digits

Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.

For example:

Given num = 38, the process is like: 3 + 8 = 11, 1 + 1 = 2. Since 2 has only one digit, return it.

Follow up:
Could you do it without any loop/recursion in O(1) runtime?

这道题很简单，就是求数根而已，但是重点却不在数根，而是你的思维，求10进制的数根求解，他们是不是有什么规律？

那么接下来就是罗列找规律：

输入：0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18.......

输出：0 1 2 3 4 5 6 7 8 9 1   2   3   4    5   6   7   8   9......

是不是很有规律？那么其中的规律就是每九个数就开始循环，循环结果是从1到9

而十进制也是+1后输出结果也+1，同时满足9后就清零

那么，也就可以看做是一个循环，可以求除9的余数，因为上面的规律就是如此！

那num%9呢？可以满足，但是得分类讨论就是当num==9或者是9的倍数的时候，那结果就得是9

代码如下：

        if(!num)

        {

            return 0;

        }

        else if(num > 0 && num % 9)

        {

            return num % 9;

        }

        else

        {

            return 9;

        }

一般看到题后自然而然就会想到使用题目中说的方法去求解

int b = num / 10;

            int a = num % 10;

            int c = 0;

            if(a + b > 9)

            {

                 c = addDigits(a + b);

            }

            else

            {

                return a + b;

            }

         return c;

这两个方式都太过繁琐,尤其是第二个还居然要使用迭代，太失败啦，根据谈论后查看的答案，没有想到居然这个还有公式

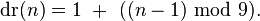
太简明啦，基础很重要啊!直接一个return 1 + (num - 1)% 9;全部搞定