本文详细介绍了哈希表的基础知识，包括哈希函数设计、Java中的hashCode方法和哈希冲突处理，特别是链地址法。文章还探讨了自定义哈希表的实现、动态空间处理以及更复杂的冲突解决策略，旨在帮助读者深入理解哈希表的工作原理和优化技巧。
哈希表
一、哈希表基础
从习题入手【题目链接】
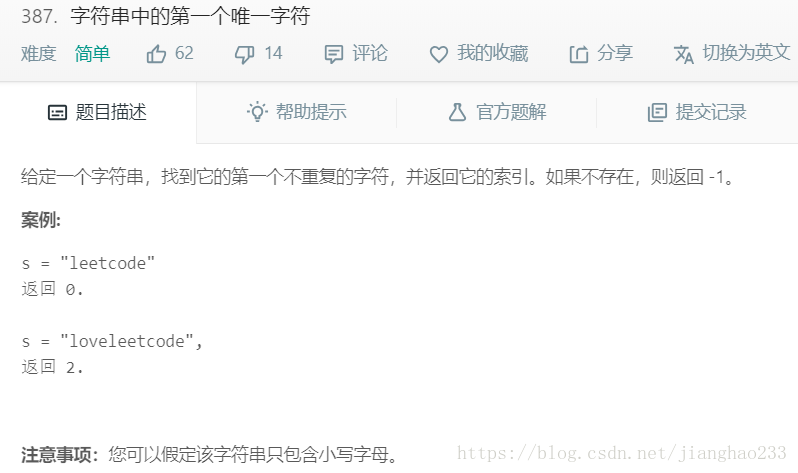
思路：可以不使用树结构来实现映射，可以直接设置包含 26个 元素的数组，对数组中每一位表示某一个字符对应的频率即可；索引为 0 的位置表示 a ，索引为 1 的位置表示 b ，以此类推。
哈希表定义：把所关心的键通过哈希函数转换为索引，然后直接把内容存在数组中即可
代码：
class Solution {
public int firstUniqChar(String s) {
int[] freq = new int[26];
for(int i = 0 ; i < s.length() ; i ++)
freq[s.charAt(i) - 'a'] ++;
for(int i = 0 ; i < s.length() ; i ++)
if(freq[s.charAt(i) - 'a'] == 1)
return i;
return -1;
}
}
输出：
int[26] freq 就是一个哈希表，每一个字符都和一个索引相对应
哈希表要解决的关键问题：1.哈希函数的设计 2. 如何解决哈希冲突 【核心思想：空间换时间；哈希表是时间和空间之间的平衡】
哈希表就是一种以 键-值(key-indexed) 存储数据的结构，我们只要输入待查找的值即key，即可查找到其对应的值。【详解】
哈希的思路很简单，如果所有的键都是整数，那么就可以使用一个简单的无序数组来实现：将键作为索引，值即为其对应的值，这样就可以快速访问任意键的值。这是对于简单的键的情况，我们将其扩展到可以处理更加复杂的类型的键。
使用哈希查找有两个步骤:
- 使用哈希函数将被查找的键转换为数组的索引。在理想的情况下，不同的键会被转换为不同的索引值，但是在有些情况下我们需要处理多个键被哈希到同一个索引值的情况。所以哈希查找的第二个步骤就是处理冲突
- 处理哈希碰撞冲突。有很多处理哈希碰撞冲突的方法，如拉链法和线性探测法。
哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制，那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1)；如果没有时间限制，那么我们可以使用无序数组并进行顺序查找，这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。
二、哈希函数的设计
“键” 通过哈希函数得到的 “索引” 分布越均匀越好
1.整型
小范围正整数直接使用
小范围负整数进行偏移
大整数：
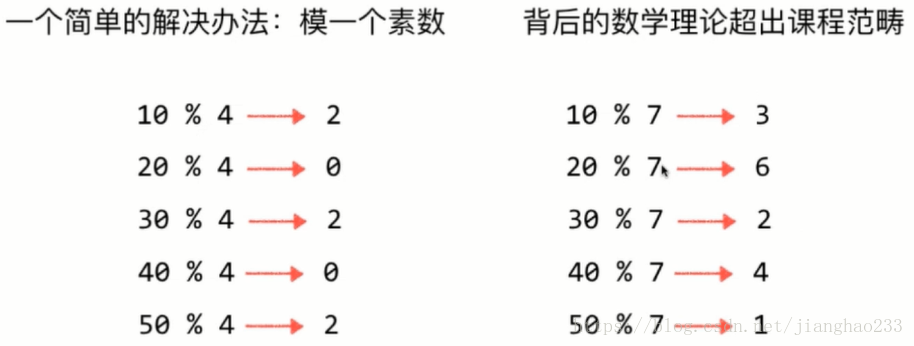
2.浮点型
在计算机中都是 32位 或 64位 的二进制表示，只不过计算机解析成了浮点数
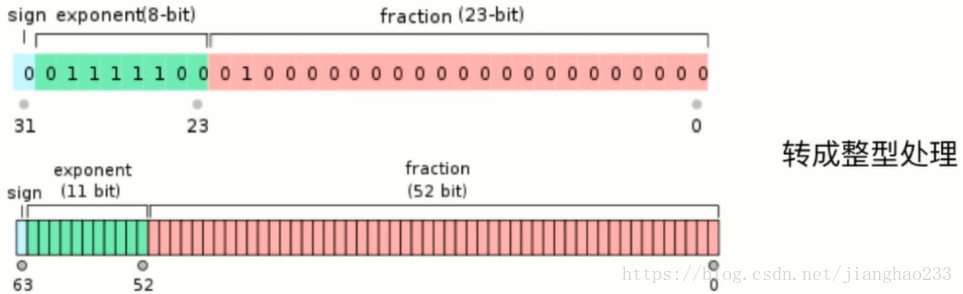
转成整型处理，再用前面的 取模 方法来处理
3.字符串
方法：转成 整型 处理
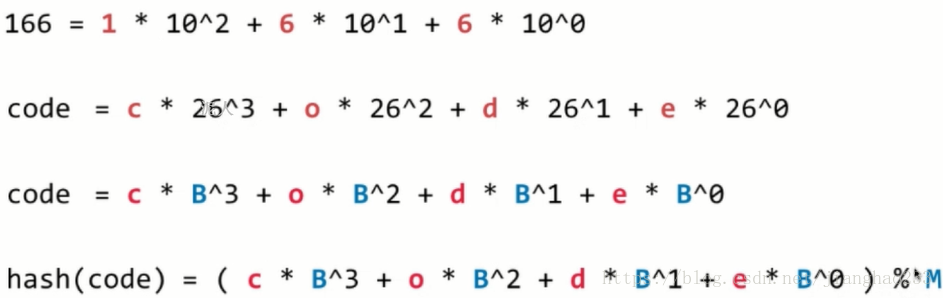
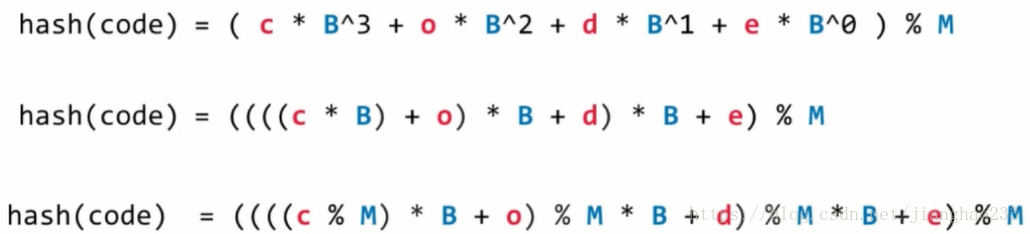
4.复合类型
方法：转成 整型 处理
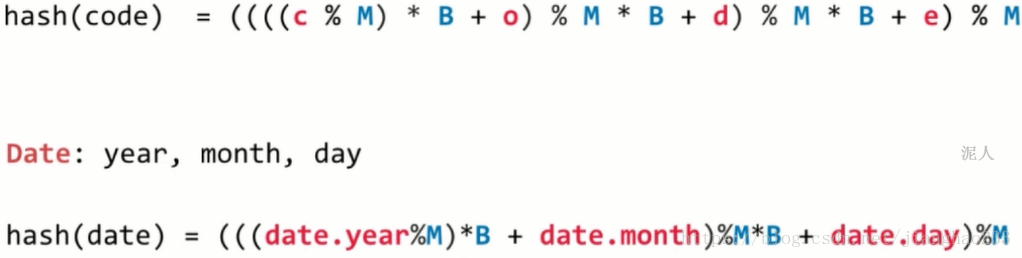
哈希函数设计原则：、
1.一致性：如果 a == b , 则 hash(a) == hash(b)
2.高效性：计算高效简便
3.均匀性：哈希值均匀分布
三、Java中的 hashCode 方法
查看 Java 中不同类型的哈希值计算方法
Main.java
import java.util.HashSet;
import java.util.HashMap;
public class Main {
public static void main(String[] args) {
int a = 42;
System.out.println(((Integer)a).hashCode());
int b = -42;
System.out.println(((Integer)b).hashCode());
double c = 3.1415926;
System.out.println(((Double)c).hashCode());
String d = "imooc";
System.out.println(d.hashCode());
System.out.println(Integer.MAX_VALUE + 1);
System.out.println();
Student student = new Student(3, 2, "Bobo", "Liu");
System.out.println(student.hashCode());
HashSet<Student> set = new HashSet<>();
set.add(student);
HashMap<Student, Integer> scores = new HashMap<>();
scores.put(student, 100);
Student student2 = new Student(3, 2, "Bobo", "Liu");
System.out.println(student2.hashCode());
}
}
自定义类：Student.java
public class Student { //复合的数据类型
int grade;
int cls;
String firstName;
String lastName;
Student(int grade, int cls, String firstName, String lastName){
this.grade = grade;
this.cls = cls;
this.firstName = firstName;
this.lastName = lastName;
}
@Override
public int hashCode(){
int B = 31;
int hash = 0;
hash = hash * B + ((Integer)grade).hashCode();
hash = hash * B + ((Integer)cls).hashCode();
hash = hash * B + firstName.toLowerCase().hashCode();
hash = hash * B + lastName.toLowerCase().hashCode();
return hash;
}
@Override
public boolean equals(Object o){
if(this == o)
return true;
if(o == null)
return false;
if(getClass() != o.getClass())
return false;
Student another = (Student)o;
return this.grade == another.grade &&
this.cls == another.cls &&
this.firstName.toLowerCase().equals(another.firstName.toLowerCase()) &&
this.lastName.toLowerCase().equals(another.lastName.toLowerCase());
}
}
输出：
四、哈希冲突的处理--链地址法 (Seperate Chaining)
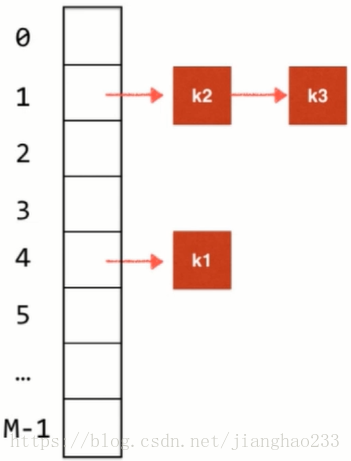
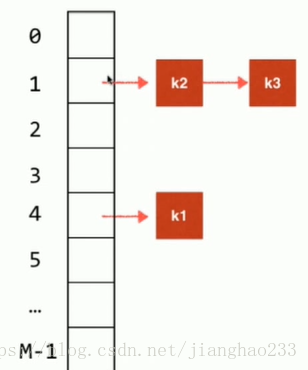
1.将 元素k1 转换为 哈希表中对应的索引值
2.假如计算后 k1 的索引对应是 4 的话，在哈希表索引为 4 的位置存储 k1
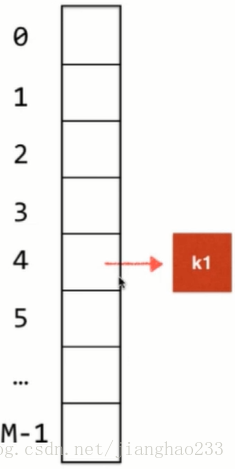
3.再加入元素 k2 ，则用相同的方法计算出索引值 为 1，插入到哈希表中
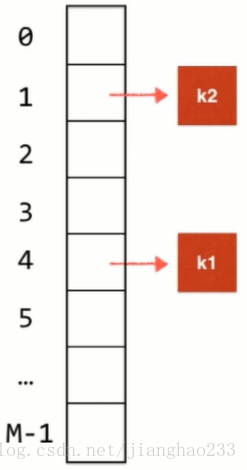
4.再加入元素 k3 ，则用相同的方法计算出索引值 为 1，产生哈希冲突，但仍然将其插入到哈希表中，将其作为 链表 即可
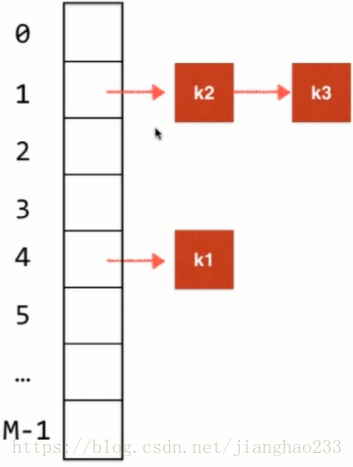
链地址法：对整个哈希表，开辟 m 个空间，对于每一个空间，由于有哈希冲突的存在，其本质上都是存储 一个链表（查找表），查找表的底层实现不一定是链表，也可以使用树结构，如图
（HashMap 本质就是一个 TreeMap 数组 / HashSet 本质就是一个 TreeSet 数组）
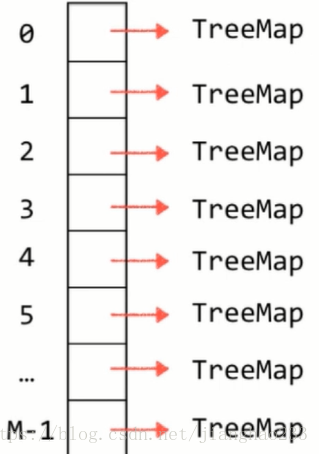
【Java8 之前，每一个位置对应一个链表，Java8 开始，当哈希冲突达到一定程度，每一个位置从链表转成红黑树】
五、实现属于我们自己的哈希表
代码实现：
HashTable.java
import java.util.TreeMap;
public class HashTable<K, V> {
private TreeMap<K, V>[] hashtable;
private int size;
private int M;
public HashTable(int M){
this.M = M;
size = 0;
hashtable = new TreeMap[M];
for(int i = 0 ; i < M ; i ++)
hashtable[i] = new TreeMap<>();
}
public HashTable(){
this(97);
}
private int hash(K key){
return (key.hashCode() & 0x7fffffff) % M;
}
public int getSize(){
return size;
}
public void add(K key, V value){ //增
TreeMap<K, V> map = hashtable[hash(key)];
if(map.containsKey(key))
map.put(key, value);
else{
map.put(key, value);
size ++;
}
}
public V remove(K key){ //删
V ret = null;
TreeMap<K, V> map = hashtable[hash(key)];
if(map.containsKey(key)){
ret = map.remove(key);
size --;
}
return ret;
}
public void set(K key, V value){ //改
TreeMap<K, V> map = hashtable[hash(key)];
if(!map.containsKey(key))
throw new IllegalArgumentException(key + " doesn't exist!");
map.put(key, value);
}
public boolean contains(K key){ //查
return hashtable[hash(key)].containsKey(key);
}
public V get(K key){
return hashtable[hash(key)].get(key);
}
}
测试时间复杂度：Main.java
import java.util.ArrayList;
public class Main {
public static void main(String[] args) {
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
// Collections.sort(words);
// Test BST
long startTime = System.nanoTime();
BST<String, Integer> bst = new BST<>();
for (String word : words) {
if (bst.contains(word))
bst.set(word, bst.get(word) + 1);
else
bst.add(word, 1);
}
for(String word: words)
bst.contains(word);
long endTime = System.nanoTime();
double time = (endTime - startTime) / 1000000000.0;
System.out.println("BST: " + time + " s");
// Test AVL
startTime = System.nanoTime();
AVLTree<String, Integer> avl = new AVLTree<>();
for (String word : words) {
if (avl.contains(word))
avl.set(word, avl.get(word) + 1);
else
avl.add(word, 1);
}
for(String word: words)
avl.contains(word);
endTime = System.nanoTime();
time = (endTime - startTime) / 1000000000.0;
System.out.println("AVL: " + time + " s");
// Test RBTree
startTime = System.nanoTime();
RBTree<String, Integer> rbt = new RBTree<>();
for (String word : words) {
if (rbt.contains(word))
rbt.set(word, rbt.get(word) + 1);
else
rbt.add(word, 1);
}
for(String word: words)
rbt.contains(word);
endTime = System.nanoTime();
time = (endTime - startTime) / 1000000000.0;
System.out.println("RBTree: " + time + " s");
// Test HashTable
startTime = System.nanoTime();
// HashTable<String, Integer> ht = new HashTable<>();
HashTable<String, Integer> ht = new HashTable<>(131071);
for (String word : words) {
if (ht.contains(word))
ht.set(word, ht.get(word) + 1);
else
ht.add(word, 1);
}
for(String word: words)
ht.contains(word);
endTime = System.nanoTime();
time = (endTime - startTime) / 1000000000.0;
System.out.println("HashTable: " + time + " s");
}
System.out.println();
}
}
输出：
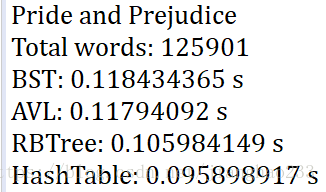
六、哈希表的动态空间处理与复杂度分析
总共有 M 个地址，如果放入哈希表的元素为 N，时间复杂度：
1.如果每个地址是链表 ：O(N/M);最坏情况：O(n)【全部发生哈希冲突】
2.如果每个地址是平衡树：O(log(N/M));最坏情况：O(log n)【全部发生哈希冲突】
如何让时间复杂度变为 O(1) :1.数组应该是动态内存分配，空间随着 n 的改变可以进行自适应（使用 resize 方法）
resize 方法：
平均每个地址承载的元素多过一定的程度，即扩容【N/M >= upperTol】
平均每个地址承载的元素少过一定的程度，即扩容【N/M < lowerTol】
HashTable.java
import java.util.Map;
import java.util.TreeMap;
public class HashTable<K, V> {
private static final int upperTol = 10; //上限
private static final int lowerTol = 2; //下限
private static final int initCapacity = 7; //初始哈希表容量
private TreeMap<K, V>[] hashtable;
private int size;
private int M;
public HashTable(int M){
this.M = M;
size = 0;
hashtable = new TreeMap[M];
for(int i = 0 ; i < M ; i ++)
hashtable[i] = new TreeMap<>();
}
public HashTable(){
this(initCapacity);
}
private int hash(K key){
return (key.hashCode() & 0x7fffffff) % M;
}
public int getSize(){
return size;
}
public void add(K key, V value){
TreeMap<K, V> map = hashtable[hash(key)];
if(map.containsKey(key))
map.put(key, value);
else{
map.put(key, value);
size ++;
if(size >= upperTol * M) //超过上限，进行扩容
resize(2 * M);
}
}
public V remove(K key){
V ret = null;
TreeMap<K, V> map = hashtable[hash(key)];
if(map.containsKey(key)){
ret = map.remove(key);
size --;
if(size < lowerTol * M && M / 2 >= initCapacity) //小于下限，进行缩容
resize(M / 2);
}
return ret;
}
public void set(K key, V value){
TreeMap<K, V> map = hashtable[hash(key)];
if(!map.containsKey(key))
throw new IllegalArgumentException(key + " doesn't exist!");
map.put(key, value);
}
public boolean contains(K key){
return hashtable[hash(key)].containsKey(key);
}
public V get(K key){
return hashtable[hash(key)].get(key);
}
private void resize(int newM){
TreeMap<K, V>[] newHashTable = new TreeMap[newM];
for(int i = 0 ; i < newM ; i ++)
newHashTable[i] = new TreeMap<>();
int oldM = M;
this.M = newM; //注意更新M
for(int i = 0 ; i < oldM ; i ++){
TreeMap<K, V> map = hashtable[i];
for(K key: map.keySet())
newHashTable[hash(key)].put(key, map.get(key));
}
this.hashtable = newHashTable;
}
}
哈希表的复杂度分析：
知哈希表均摊时间复杂度为：O(1)
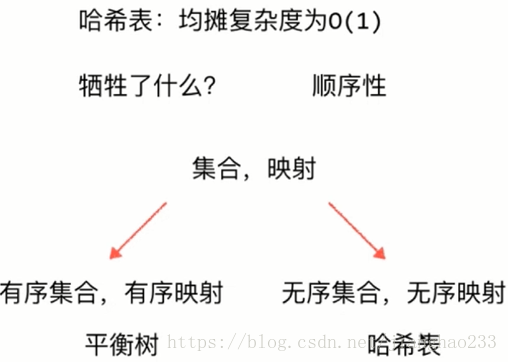
代码中的Bug: Comparable(可比较性矛盾)
七、哈希表更复杂的动态空间处理方法
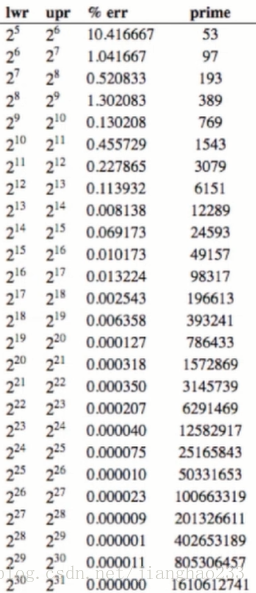
扩容 M--2*M ,但 2*M 可能不是 素数 了，但希望 哈希表 的空间最好是 素数；
解决方法：不要简单的 *2，而是根据下表，超过 53 就扩容为 97 ，超过 97 就扩容为 193，以此类推。
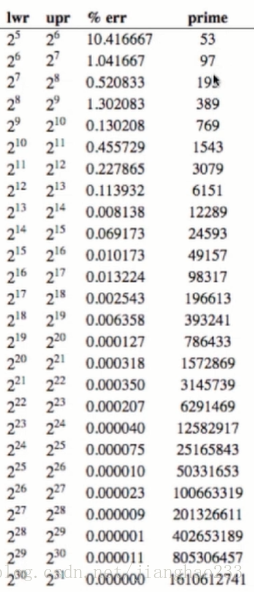
八、更多哈希冲突的处理方法
1.开放地址法
在链地址法中，每一个键计算出哈希值之后，哈希值索引所在的地址只属于所属的哈希值等于这个索引相应的元素【封闭地址】
开放地址法和上述方法相反，对于哈希表中的每一个地址，所有哈希值的元素都有机会进入
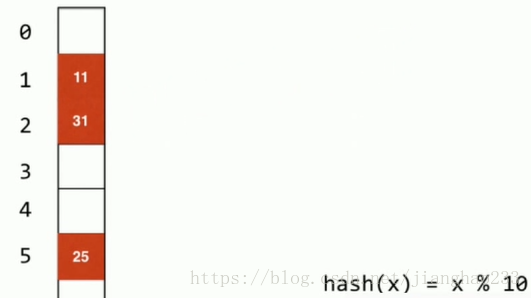
每一个地址就是直接存元素，11 和 31 产生哈希冲突，就从索引为 1 的地方向下找，空的地方是索引为 2 的地方，故将 31 放在 2 中；
再插入元素 81，发生哈希冲突，原理同上，插入到索引 3 的位置【此方法：线性探测，遇到哈希冲突 +1】
平方探测：遇到哈希冲突 +1 +4 + 9 ...【提高性能】
二次哈希：遇到哈希冲突 +hash2(key)
更多方法：
总结：
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
