代码随想录算法训练营Day26 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树

目录

669. 修剪二叉搜索树

108.将有序数组转换为二叉搜索树

538.把二叉搜索树转换为累加树

669. 修剪二叉搜索树

题目

669. 修剪二叉搜索树 - 力扣（LeetCode）

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例1：

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例2：

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

• 树中节点数在范围 [1, 104] 内
• 0 <= Node.val <= 104
• 树中每个节点的值都是 唯一 的
• 题目数据保证输入是一棵有效的二叉搜索树
• 0 <= low <= high <= 104

思路

视频讲解：LeetCode：669. 修剪二叉搜索树

代码随想录：669.修剪二叉搜索树

注意点：并不是只要遇到一个不满足条件的节点就返回null，而是继续判断其孩子是否满足条件，如图：

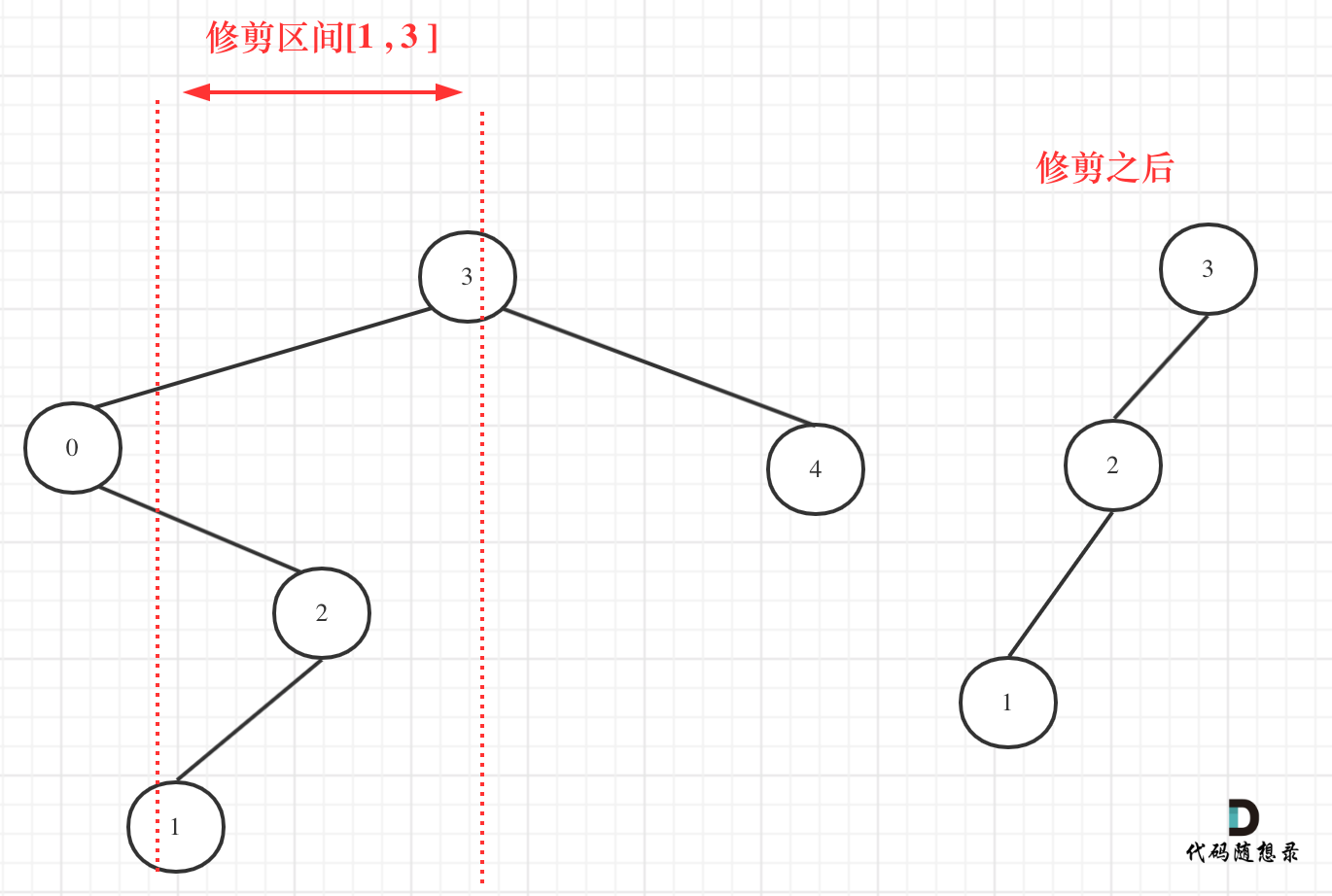
题解

独立题解（很多判断条件和步骤可以省去）：

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null)
            return null;
        if (root.val < low) {
            if (root.right == null)
                return null;
            if (root.right != null) {
                root = trimBST(root.right,low,high);
                return root;
            }
        }else if (root.val > high) {
            if (root.left == null)
                return null;
            if (root.left != null) {
                root = trimBST(root.left,low,high);
                return root;
            }
        }
        if (root!=null&&root.val >= low && root.val <= high) {
            root.left = trimBST(root.left, low, high);
            root.right = trimBST(root.right, low, high);
        }
        return root;
    }
}

优化后：

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null)
            return null;
        if (root.val < low) {
            root = trimBST(root.right, low, high);
            return root;
        } else if (root.val > high) {
            root = trimBST(root.left, low, high);
            return root;
        }
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

108.将有序数组转换为二叉搜索树

题目

108. 将有序数组转换为二叉搜索树 - 力扣（LeetCode）

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

示例1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]

解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 按 严格递增 顺序排列

思路

视频讲解：LeetCode：108.将有序数组转换为二叉搜索树

代码随想录：108.将有序数组转换为二叉搜索树

注意题目要求为平衡二叉树，递归过程中先创建根节点，再创建左子树和右子树，最后返回根节点。

题解

独立题解：

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return sortedArrayToBST(nums, 0, nums.length - 1);
    }

    TreeNode sortedArrayToBST(int[] nums, int start, int end) {
        if (start > end)
            return null;
        int index = (end + start) / 2;
        TreeNode root = new TreeNode(nums[index]);
        root.left = sortedArrayToBST(nums, start, index - 1);
        root.right = sortedArrayToBST(nums, index + 1, end);
        return root;
    }
}

538.把二叉搜索树转换为累加树

题目

538. 把二叉搜索树转换为累加树 - 力扣（LeetCode）

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

示例1：

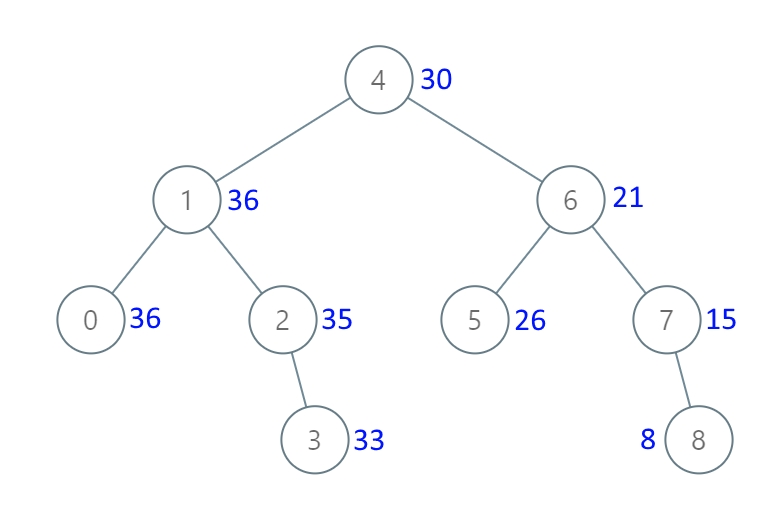
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例2：

输入：root = [0,null,1]
输出：[1,null,1]

示例3：

输入：root = [1,0,2]
输出：[3,3,2]

示例4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

• 树中的节点数介于 0 和 104 之间。
• 每个节点的值介于 -104 和 104 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

思路

代码随想录：538.把二叉搜索树转换为累加树

视频讲解：LeetCode：538.把二叉搜索树转换为累加树

按照右中左顺序遍历。

题解

独立题解：

class Solution {
    int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        if(root==null)
            return null;
        convertBST(root.right);
        sum+=root.val;
        root.val = sum;
        convertBST(root.left);
        return root;
    }
}