《算法笔记》读书记录DAY_7

最新推荐文章于 2025-12-02 22:37:42 发布

原创最新推荐文章于 2025-12-02 22:37:42 发布 · 107 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #排序算法

算法学习专栏收录该内容

63 篇文章

订阅专栏

本文介绍了归并排序和快速排序两种经典排序算法。归并排序采用分治策略，以O(nlogn)时间复杂度实现排序。快速排序则通过一趟排序将序列分隔成两部分，并对每一部分递归地进行排序，最终达到全序列有序。文章提供了算法的基本思想和示例代码。

CHAPTER_4 算法初步入门

4.6.2 归并排序

归并排序是一种基于归并思想的排序方法，它以O(nlogn)的时间复杂度将无序序列排成有序。本节主要介绍最基本的2路归并。

2路归并的思想：采用分治的策略，将序列两两分组，这样序列初始被分为 $[\frac{n}{2}]$ 个组，每个组内单独排序，保证组内有序；再将这些组两两归并为 $[\frac{n}{4}]$ 个组，每个组内再排序；...；以此类推，直到最后归并为一个组，再给这个组排序。

如下面例子：

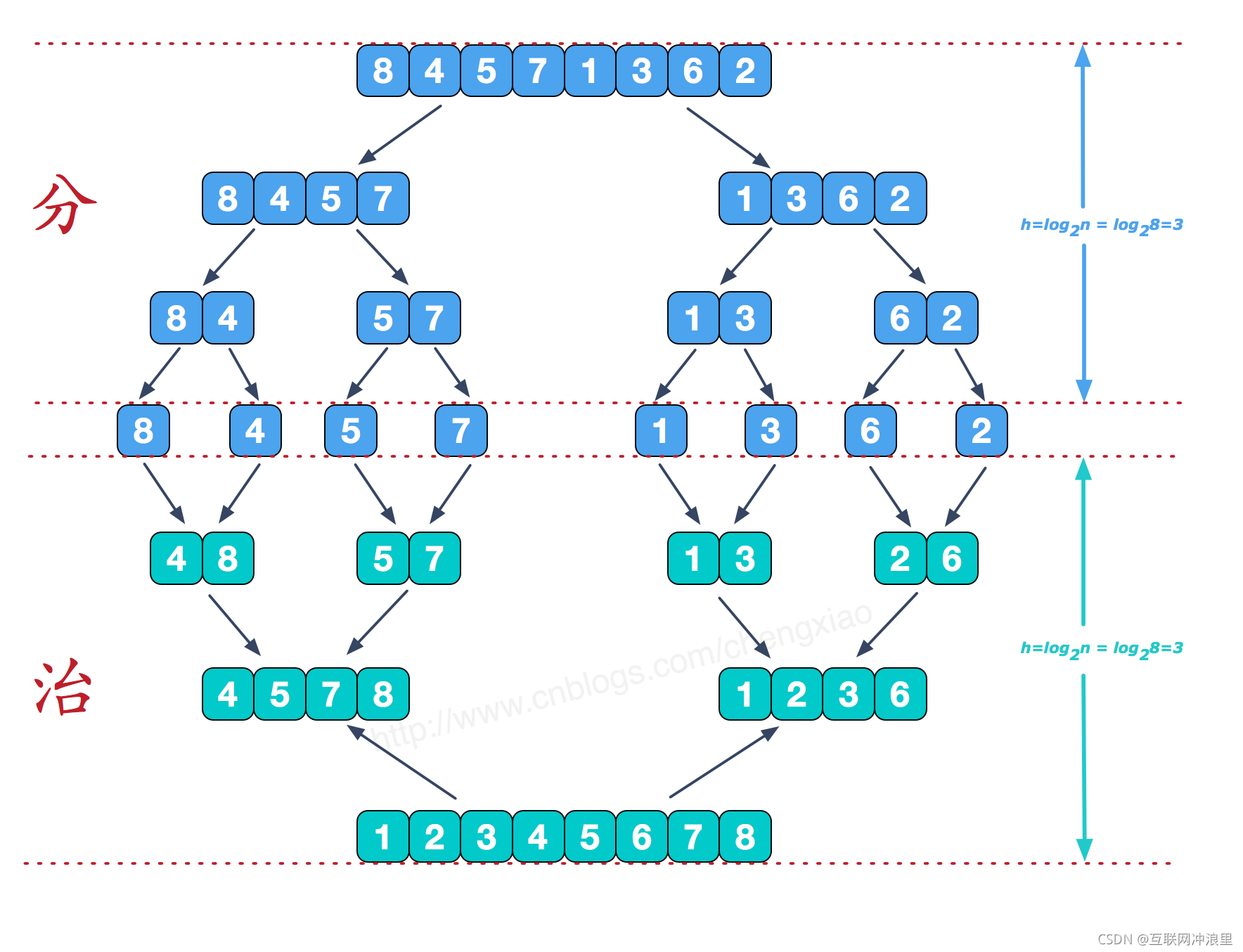
参考代码（递归实现）：

递归的写法很容易，只需反复将当前区间[left,right]分为两半，对两个子区间[left,mid]与[mid+1,right]分别归并排序。待两个子区间有序后将其合并成一个有序区间，而合并的方法实际在4.6.1节中已经实现。

const int maxn=100;

void merge(int a[],int L1,int R1, int L2,int R2) {    //将a序列的区间[l1,r1]与[l2,r2]合并成一个有序序列 
	int i=L1,j=L2;                                    //i和j指向两个区间的起始位置 
	int tmp[maxn],count=0;                            //tmp为临时数组，暂时存放合并后的有序序列
	while(i<=R1&&j<=R2) {
		if(a[i]<=a[j])
			tmp[count++]=a[i++];
		else
			tmp[count++]=a[j++];
	}
	while(i<=R1) {
		tmp[count++]=a[i++];		
	}
	while(j<=R2) {
		tmp[count++]=a[j++];			
	}
	for(i=L1;i<=R2;i++) {
		a[i]=tmp[i-L1];
	}                                                  //将tmp数组赋值回a[] 
}

void mergeSort(int a[],int left,int right) {     //归并排序函数 
	if(left<right) {
		int mid=(left+right)/2;
		mergeSort(a[],left,mid);
		mergeSort(a[],mid+1,right);
		merge(a[],left,mid,mid+1,right);	
	}
	return;
}

4.6.3 快速排序

快排基本思想：通过一趟排序将待排序列分隔成独立的两组，其中一组内的元素均比另一组的元素小。同样的，分别对每个组内部继续进行排序，通过一趟排序将一组序列再次分成两个更小组，分隔后的一组元素也比另一组小。依次类推，直至分割至最小值，整个序列有序。

算法思路：

（1）在数组中随机选一个基准数；

（2）将数组中小于基准数的数据移到基准数左边，大于基准数的移到右边；

（3）对于基准数左、右两边的数组，不断重复以上两个过程，直到每个子集只有一个元素，即为全部有序。

如下例：给序列arr={23,45,17,11,13,89,72,26,3,17,11,13}进行一趟快排，基准数用temp记录（初始选择第一个元素）

（1）先将arr[1]存放至temp，令i,j指向序列的首尾；

（2）只要arr[j]>temp，就将j不断左移，当某个时候arr[j]<=temp时，令arr[i]=arr[j]。然后保持j不动，处理下标i。

（3）只要arr[i]<temp，就将i不断右移，当某个时候arr[i]>temp时，令arr[j]=arr[i]。然后保持i不动，处理下标j。

（4）循环重复(2)(3)两步，直至i=j（即两下标相遇），令a[i]=temp。一趟快排结束，temp左边的组元素小于右边的组元素。

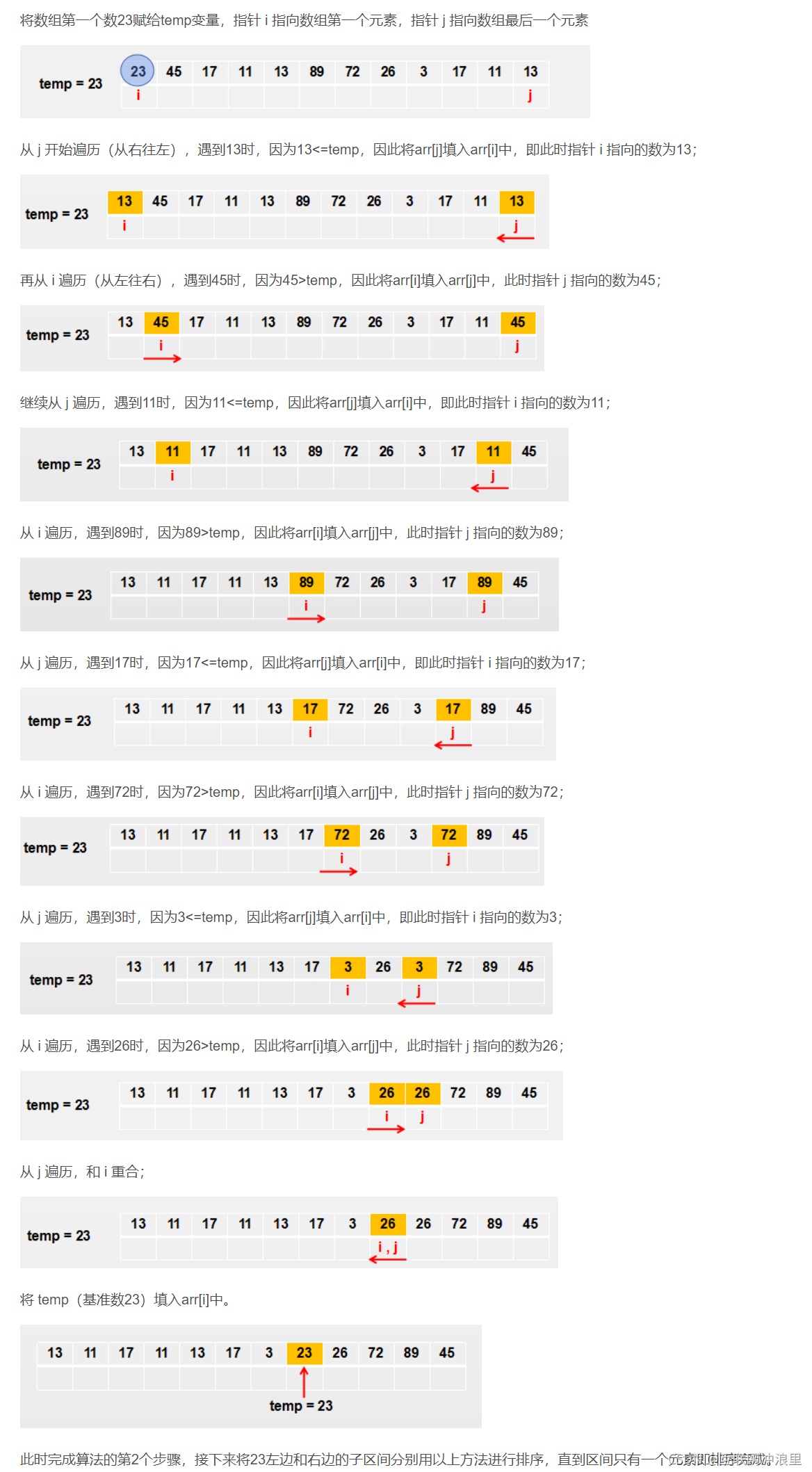
参考代码：

在实现代码之前，我们先要明确一点。上述例子的temp初始值选择的是序列的第一个元素，实际上初始基准数选择随机数更优。C实现随机数需要包含头文件<stdlib.h>和<time.h>。要生成一个[a,b]范围内的随机数，我们使用语句(int)(round(1.0*rand()/RAND_MAX*(b-a)+a))。

void swap(int &x,int &y) {                                      //交换函数 
	int tmp=x;
	x=y;
	y=tmp;
}

int partition(int A[],int left,int right) {                     //一趟快排 
	int p=(int)(round(1.0*rand()/RAND_MAX*(right-left)+left));  //生成范围在[left,right]内的随机数,作为基准值
	swap(A[p],A[left]);                                         //把基准值换到第一个去，便于算法统一 
	int tmp=A[left];                                            //把基准值存入临时变量
	while(left<right) {
		while(A[right]>tmp&&left<right)
			right--;
		A[left]=A[right];
		while(A[left]<=tmp&&left<right)
			left++;
		A[right]=A[left];
	}
	A[left]=tmp;
	return left;                                                //范围基准值的位置
}

void quickSort(int A[],int left,int right) {
	if(left<right) {
		int pos=partition(A,left,right);
		quickSort(A,left,pos-1);
		quickSort(A,pos+1,right);
	}
}