剑指 Offer 40. 最小的k个数(随机选择算法)

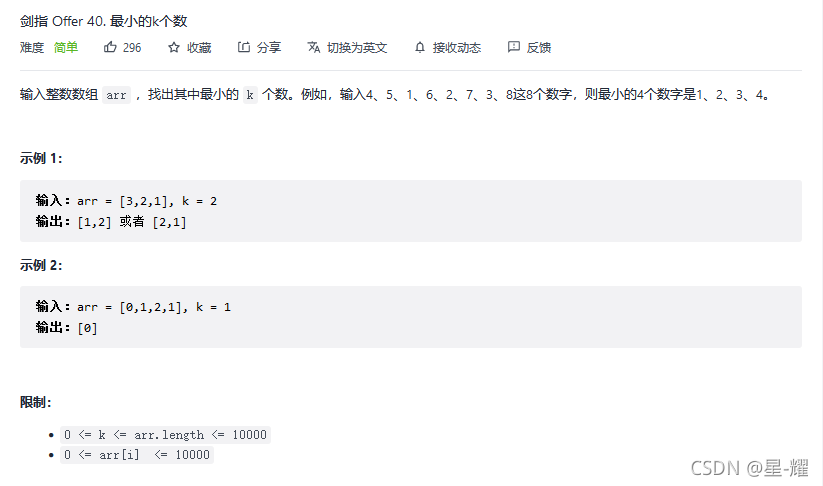
解法：随机选择算法
随机选择算法建立在快排的基础上。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 // 选择主元，进行分区
 int partion(int *arr, int left, int right)
 {
     int temp = arr[left];
     while(left < right)
     {
         while(left < right && arr[right] > temp) right--;
         arr[left] = arr[right];
         while(left < right && arr[left] <= temp) left++;
         arr[right] = arr[left];
     }
     arr[left] = temp;
     return left; // 返回相遇的下标，左边的都比它小，右边的都比它大
 }
 // 交换两整数
 void swap(int *a, int *b)
 {
     int temp = *a;
     *a = *b;
     *b = temp;
 }
 // 随机选择主元
 int randPartion(int *arr, int left, int right)
 {
     int num = 1.0*rand()/RAND_MAX*(right-left)+left;
    swap(&arr[left],&arr[num]);
    return partion(arr, left, right);
 }
 // 返回第k大的坐标
int randSelect(int *arr, int left, int right, int k)
 {
     if(left == right) return left;
     int p = randPartion(arr, left, right);
     int m = p - left + 1; // 区间[left, right]的第m大
     if(k == m) return p; // 找到第k大的坐标p，直接返回
     else if(k < m) 
     {
         return randSelect(arr, left, p-1, k);
     }
     else
     {
        return randSelect(arr, p+1, right, k-m);
     }
 }
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){
    // 处理非法输入
    if(k == 0)
    {
        *returnSize = 0;
        return arr;
    }
    int index = randSelect(arr, 0, arrSize-1, k);
    *returnSize = index + 1;
    return arr;
}

虽然随机选择算法的最坏时间复杂度是$O(n^2)$，但其对任意输入的期望时间复杂度却是$O(n)$。（算法笔记：胡凡）