剑指 Offer 10- I. 斐波那契数列

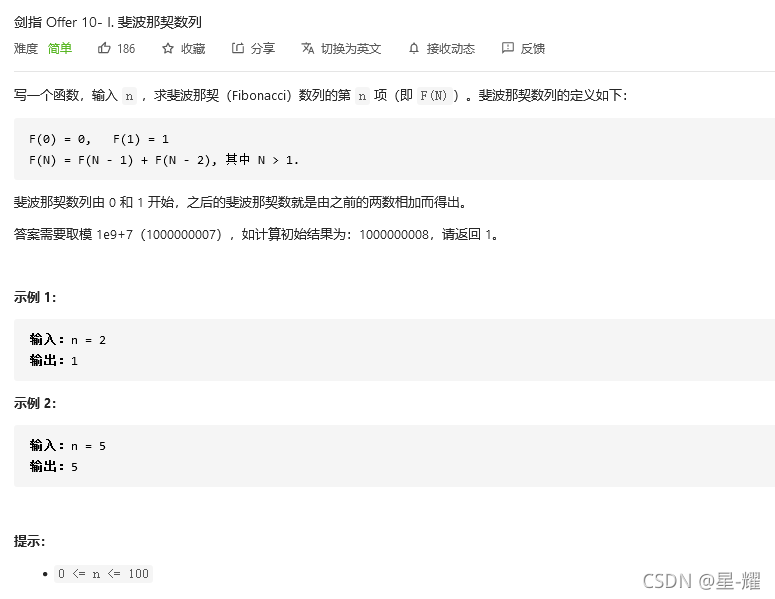
传统办法是递归计算，但是当n比较大时，会收到递归深度的限制。同时，可以发现，在递归中存在重复计算问题。

改进：
（1）通过记忆前两个状态，避免重复计算，
（2）改递归为迭代

int fib(int n){
    if(n==0 || n==1) return n;
    // 从f(2)开始迭代算到f(n)
    int f0 = 0;
    int f1 = 1;
    for(int i=2; i<=n; i++)
    {
        f1 = f0 + f1;
        f0 = f1 - f0;
        f1 = f1 % 1000000007;
    }
    return f1;
}

时间复杂度$O(n)$，空间复杂度$O(1)$。