洛谷刷题——P1146 硬币翻转

题目：来源于洛谷

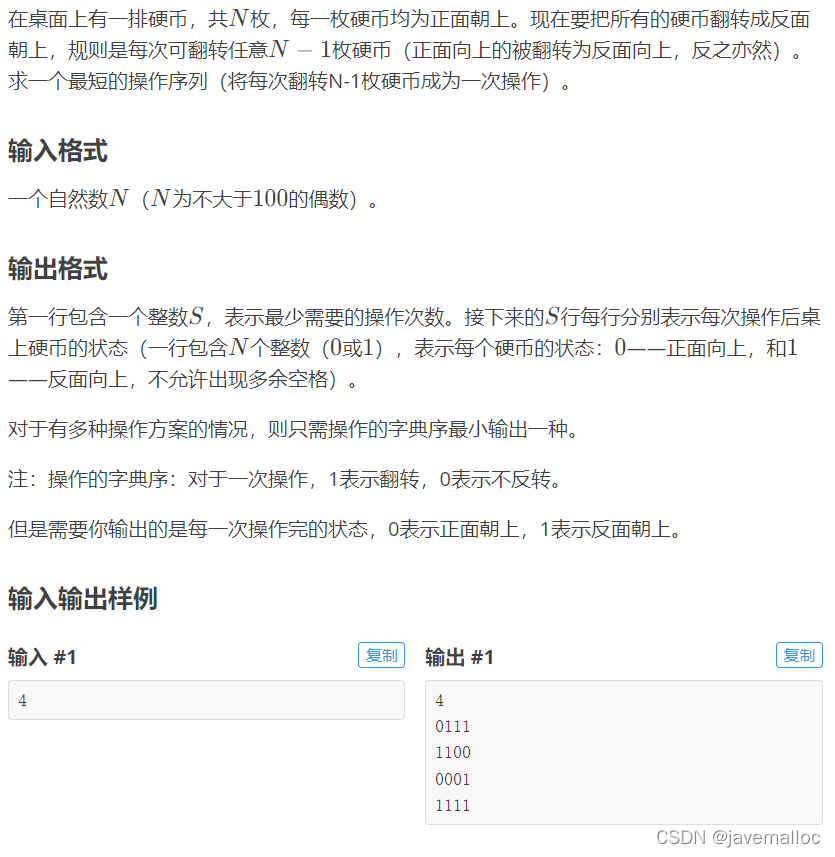
分析：
n是偶数

首先，我们需要明白，一枚硬币反转了奇数次，那么它一定被反转了

其次，每次反转n-1枚硬币，那么意味着每次有1枚硬币没反转，所以 每次反转n-1枚硬币 等效于 每次有1枚硬币没反转

如果把每枚硬币都反转了n-1次（也就是奇数次），那么就完成所有硬币的反转

最后，我们总共反转n次，就可以实现每次有1枚硬币没有反转。等反转完n次之后，每枚硬币就都反转了n-1次

上代码：

#include <iostream>
#include <cstdio>
#include <bitset>

using namespace std;

bitset<101> bt;

int main()
{
	
	int n;
	cin >> n;
	cout << n << endl;

	//外层控制输出多少组数据
	for (int i = 1; i <= n; ++i) {

		//内层控制 每次反转：除了第i枚硬币，其他硬币都要被反转
		for (int j = 1; j <= n; ++j) {

			//第i次反转的 第i枚硬币不反转
			if (j == i) {
				cout << bt[i];
				continue;
			}

			//如果 第j枚硬币为 1 反面朝上， 反转过来 0 反面朝上
			if (bt[j]) {
				bt[j] = 0;
			}
			else {
				bt[j] = 1;
			}
			cout << bt[j];
		}
		cout << endl;
	}

	return 0;
}

刚开始我没用bitset，而是用bool数组，结果发现出错了，等会我再看看原因

先去吃饭先，溜了溜了 U•ェ•*U