洛谷刷题——P1047 [NOIP2005 普及组] 校门外的树

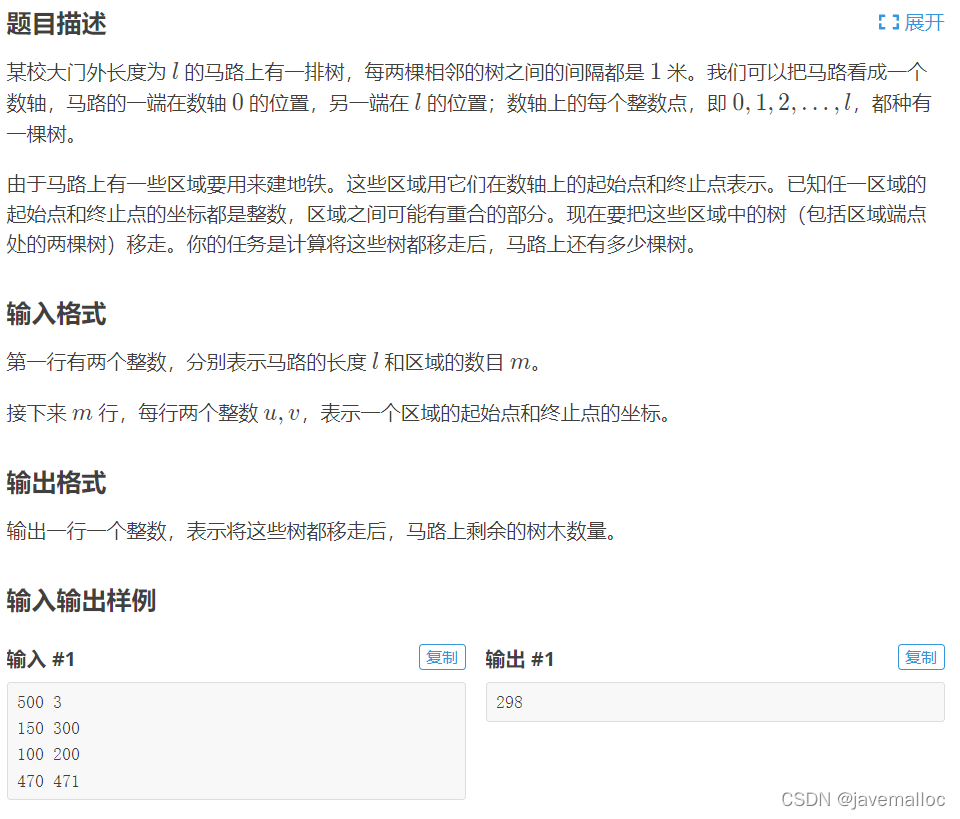
题目：来源于洛谷

分析：
看了题目之后，要求输出剩下的数。而树分为砍和不砍，可以使用bitset，那什么是bitset呢？

bitset是一串二进制码（只含0和1，长度自己设），当然使用bitset需要包含头文件 bitset 。

定义方式：bitset < n > name，n是长度，name是名字；定义好之后，默认里面存的都是0

话不多说，上代码：

#include <iostream>
#include <cstdio>
#include <bitset>

using namespace std;

bitset<1005> bt;

int main()
{

	//输入

	int len, m;
	cin >> len >> m;

	//外层循环，控制输入几组数据
	
	for (int i = 0; i < m; ++i) {
		
		int start, end;			//开始区间 和 结束区间
		cin >> start >> end;

		//内层循环，把bt里面的值改为1，也就是把树砍了
		for (; start <= end; ++start) {
			bt[start] = 1;
		}

	}

	//统计没有砍的树

	int count = 0;

	for (int i = 0; i <= len; ++i) {
		if (!bt[i]) {
			count++;
		}
	}

	cout << count << endl;

	return 0;
}

继续刷题ing （＞人＜；）