机器学习入门02-朴素贝叶斯原理和java实现

        朴素贝叶斯是一种基于概率统计的机器学习方法，其原理采用计算样本数据中先验数据与标签数据出现的概率，以先验数据对应最大出现概率的标签作为预测结果。

        朴素贝叶斯公式一般记为：P(A|B)=P(A)*P(B|A)/P(B)，即当我们要预测先验条件B出现时A出现的概率时，可以通过条件A出现概率与条件A出现时条件B出现概率的乘积除以条件B的概率。在计算中P(A)*P(B|A)等效于计算条件A与条件B同时出现概率，即P(A∩B)。

        也就是说，朴素贝叶斯的训练过程主要就是统计条件概率P(B)和联合概率P(A∩B)，由于朴素贝叶斯是统计各种条件出现概率，对条件本身数据格式没有具体要求，因此适用于文本型数据的预测，可以应用于邮件过滤、新闻分类等方面。

        训练数据由标签和先验条件组成，这里假定一组训练数据，结果标签由1、2、3表示，先验条件假设两个维度，第一个维度由A、B、C、D组成，第二个维度由a、b、c、d组成。

如图：

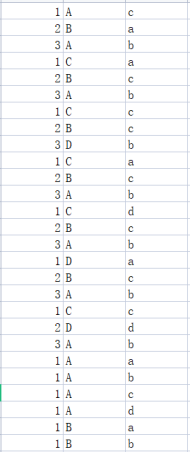
        第一步是读取训练数据，训练数据为csv格式，读取数据时使用逗号分割标签数据和不同维度数据。

读取训练数据：

public List<List<String>> readTrainFile(File trainFile) throws Exception {
		List<List<String>> resultList = new ArrayList<List<String>>();
		if (trainFile.exists()) {
			BufferedReader reader = new BufferedReader(new FileReader(trainFile));
			String line;
			while ((line = reader.readLine()) != null) {
				String[] strings = line.split(",");
				List<String> lineList = new ArrayList<String>();
				for (int i = 0; i < strings.length; i++) {
					lineList.add(strings[i]);
				}
				resultList.add(lineList);
			}
			reader.close();
		}
		return resultList;
	}

第二步，计算联合概率：

private Map<String, Double> caculateUnionProbability(List<List<String>> trainData) {
		Map<String, Double> result = new HashMap<String, Double>();
		int dataSize = trainData.size();
		double singleProbability = 1 / (double) dataSize;
		for (int i = 0; i < dataSize; i++) {
			List<String> line = trainData.get(i);
			if (null != line) {
				String key = new String();
				for(int j = 0; j < line.size(); j++) {
					key += line.get(j);
				}
				if (result.containsKey(key)) {
					result.put(key, result.get(key) + singleProbability);
				} else {
					result.put(key, singleProbability);
				}
			}
		}
		return result;
	}

第三步，计算条件概率：

private Map<String, Double> caculateConditionProbability(List<List<String>> trainData) {
		Map<String, Double> result = new HashMap<String, Double>();
		int dataSize = trainData.size();
		double singleProbability = 1 / (double) dataSize;
		for (int i = 0; i < dataSize; i++) {
			List<String> line = trainData.get(i);
			line.remove(0);
			if (null != line) {
				String key = new String();
				for(int j = 0; j < line.size(); j++) {
					key += line.get(j);
				}
				if (result.containsKey(key)) {
					result.put(key, result.get(key) + singleProbability);
				} else {
					result.put(key, singleProbability);
				}
			}
		}
		return result;
	}

第四步，将训练结果写入模型文件：

private void writeTrainResult(List<String> tags,Map<String, Double> unionProbability, Map<String, Double> conditionProbability,
			File resultFile) throws Exception {
		resultFile.createNewFile();
		FileWriter writer = new FileWriter(resultFile);
		for (int i = 0; i < 3; i++) {
			if (i == 0) {
				String allTag = new String();
				for (int j = 0; j < tags.size(); j++) {
					String tag = tags.get(j);
					if(j < tags.size() - 1) {
						allTag += tag + ",";
					}else {
						allTag += tag;
					}
				}
				allTag = "tags-" + allTag;
				writer.write(allTag);
				writer.write("\r\n");
			}else if (i == 1) {
				// 写入联合概率
				List<String> keyList = new ArrayList<String>();
				Set<String> keys = unionProbability.keySet();
				Iterator<String> iterator = keys.iterator();
				String firstKey = iterator.next();
				keyList.add(firstKey);
				while (iterator.hasNext()) {
					String key = iterator.next();
					keyList.add(key);
				}
				for (int j = 0; j < keyList.size(); j++) {
					String key = keyList.get(j);
					Double value = unionProbability.get(key);
					writer.write(key + "-" + value.toString());
					writer.write("\r\n");
				}
			} else {
				// 写入条件概率
				List<String> keyList = new ArrayList<String>();
				Set<String> keys = conditionProbability.keySet();
				Iterator<String> iterator = keys.iterator();
				String firstKey = iterator.next();
				keyList.add(firstKey);
				while (iterator.hasNext()) {
					String key = iterator.next();
					keyList.add(key);
				}
				for (int j = 0; j < keyList.size(); j++) {
					String key = keyList.get(j);
					Double value = conditionProbability.get(key);
					writer.write(key + "-" + value.toString());
					writer.write("\r\n");
				}
			}
		}
		writer.close();
	}

第五步，预测：

public String predict(File resultFile, String conditionB) throws Exception{
		String result = new String();
		Map<String, Double> results = new HashMap<String, Double>();
		String[] conditionAll = getAllCondition(resultFile);
		//分别计算不同分类对应概率
		for(int i = 0; i < conditionAll.length; i++) {
			String condition = conditionAll[i];
			String unionCondition = condition + conditionB;
			double res = predictProbability(resultFile, conditionB,unionCondition);
			results.put(condition, res);
		}
		//取出最大概率对应分类作为结果
		double max = 0;
		for(int i = 0; i < results.size(); i++) {
			double res = results.get(conditionAll[i]);
			if (res > max) {
				max = res;
				result = conditionAll[i];
			}
		}
		return result;
	}
测试：
//测试
	public static void main(String[] args) throws Exception {
		NaiveBaysian naiveBaysian = new NaiveBaysian();
		naiveBaysian.train(new File("C:/Users/admin/Desktop/1.txt"), new File("C:/Users/admin/Desktop/2.bys"));
		String result = naiveBaysian.predict(new File("C:/Users/admin/Desktop/2.bys"), "Da");
		System.out.println(result);
		
	}

       测试中训练模型和预测是一起做的，实际应用中，只需要读取训练好的模型文件，用预测部分代码即可完成朴素贝叶斯的计算。