论文阅读《Symmetric Cross Entropy for Robust Learning with Noisy Labels》

最新推荐文章于 2023-12-09 04:53:48 发布

原创最新推荐文章于 2023-12-09 04:53:48 发布 · 5.1k 阅读

11 ·

CC 4.0 BY-SA版权

noisy label 专栏收录该内容

1 篇文章

订阅专栏

本文介绍了ICCV19论文中针对噪声标签问题，通过结合Symmetric Cross Entropy (SL)损失，改进了传统交叉熵在处理易类和硬类上的不足。SL利用KL散度的对称性，使得模型对噪声标签更稳健，实验证明其性能优于经典损失。关键概念包括易类、硬类、Reverse Cross Entropy (RCE) 和SLloss的计算。

论文链接：https://arxiv.org/abs/1908.06112

ICCV19的一篇文章，跟Nosiy Label相关。noisy label指的是质量再高的数据集中，难免也会存在一些错误的标注，而这些错误标注会对DNN的训练带来影响。在本文中，作者揭示了传统用作分类的交叉熵CE损失函数的弊端：即在一些easy class会对nosiy label过拟合，同时一些hard class学习的也不够充分。

因此作者根据KL散度的非对称性，提出了一种Symmetric cross entropy Learning（SL）的方法，使传统的CE和Reverse Cross Entropy（RCE）损失函数相结合。RCE是一种noise robust的损失函数，形式上与CE对称。实验证明这种SL的方法performance优于其他经典的loss。

CE的问题

在这里插入图片描述
easy class就是上图中cluster相对独立的class，由于学习的比较好，feature分得相对较开。而hard class就是不同类别feature杂糅在一起的class，学习的不够充分。可以看到CE-clean效果还可以，但存在一些hard class；而一旦存在noisy label，CE的feature分布立刻就拉垮了，很多class杂糅到了一起，导致performance下降；使用SL方法，即使有40%的noisy label，特征分得依然很开，而且杂糅到一起的hard class也不是很明显。

所以上述的两个问题就是CE的缺点：（1）hard class处理不好；（2）遇到noisy label表现下降很多。

Symmetric Cross Entropy Loss

作者受KL散度启发，KL散度衡量的是两个distribution之间的差异：
在这里插入图片描述
q表示GT，p表示预测值，这里可以把类别看作是一个distribution。由于KL散度是非对称的，所以 $K L (q ∣ ∣ p)$ 表示的是让p不断向q靠近而计算的penalty。但是如果q属于noisy label，就无法表示正确的class分布了，而此时p一定程度上可以表示正确的class分布。所以这里考虑KL散度的反方向 $K L (p ∣ ∣ q)$ 。因此将两个方向的KL散度计算式相结合：
在这里插入图片描述
同样的，可以将KL散度的计算公式推广到交叉熵损失函数上面：

而这里Reverse Cross Entropy（RCE）损失函数可以定义为：

所以总的SCE loss的计算式如下：

这里RCE损失是noisy tolerant的，而CE损失对noisy label敏感，但是他对于模型的收敛有着推动作用。于是这两个loss之间要按照一定的比例做加权，得到SL loss：
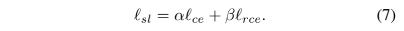
在这里插入图片描述
在公式5中的 $l o g q$ 可能会是 $l o g 0$ ，这种情况下令 $l o g 0 = A$ ，A通常是一个小于0的值。

Theoretical Analysis

$x$ 表示数据集， $y$ 表示clean label， $\hat{y}$ 表示noisy label;

clean label的风险定义为 $R(f)=E_{x,y}l_{rce}$ ，noise rate为 $\eta$ 的风险为 $R^{\eta}(f)=E_{x,\hat{y}}l_{rce}$ ;

$f^{*}$ 和 $f^{*}_{\eta}$ 是 $R (f)$ 和 $R^{\eta}(f)$ 的全局最小值。

有了这些条件，可以开始证明了：

证明部分脑洞略大，不复杂，懒得写了，参考该文章。

Experiment

在这里插入图片描述
引入SL以后，使模型变得noisy tolerant，对于easy class收敛更快，对于hard class收敛更优。

在这里插入图片描述

总结

对于noisy label问题，作者分析了传统分类损失CE的缺点，并受KL散度的启发，引入了一个和CE对称的RCE Loss。RCE经实验和理论论证，属于一个noisy tolerant的loss，将其与收敛能力更强的CE相结合，就是本文应对noisy label的策略。私认为noisy label这个方向虽然小众，但是在工业界应该会有不错的前景。