自顶向下的归并排序（Merge Sort) O(nlogn)

最新推荐文章于 2024-09-15 10:42:58 发布

原创最新推荐文章于 2024-09-15 10:42:58 发布 · 1.4k 阅读

2 ·

CC 4.0 BY-SA版权

数据结构和算法专栏收录该内容

6 篇文章

订阅专栏

本文详细介绍了归并排序的基本思想及其实现过程，并通过图例解释了如何将数组逐步拆分和归并，最后给出了C++代码实现。

归并排序的基本思想:

该算法是采用分治法来实现的，将原来的数组不断对半分，直到分得每个数组含有一个元素后，再一层一层归并的过程（按要求排列好）

下面就是将数组逐渐二分的过程：

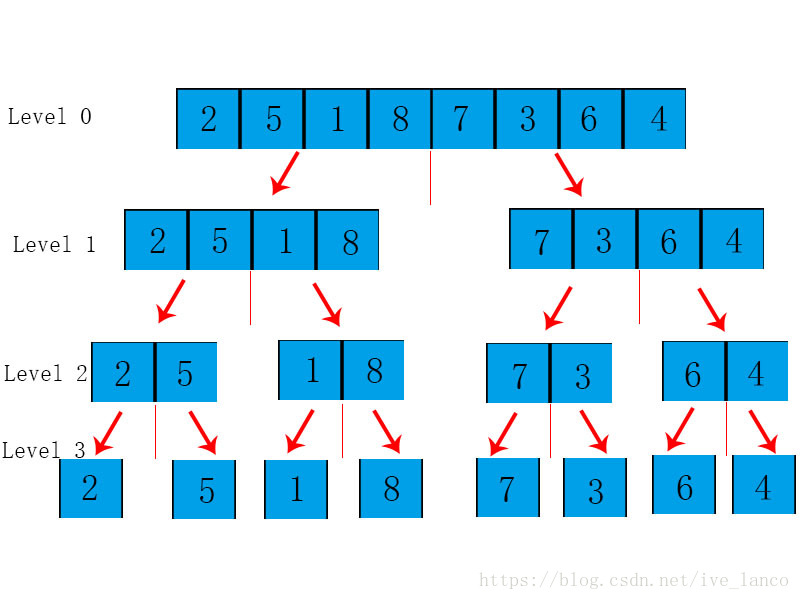
对Level 3到Level2 的归并：

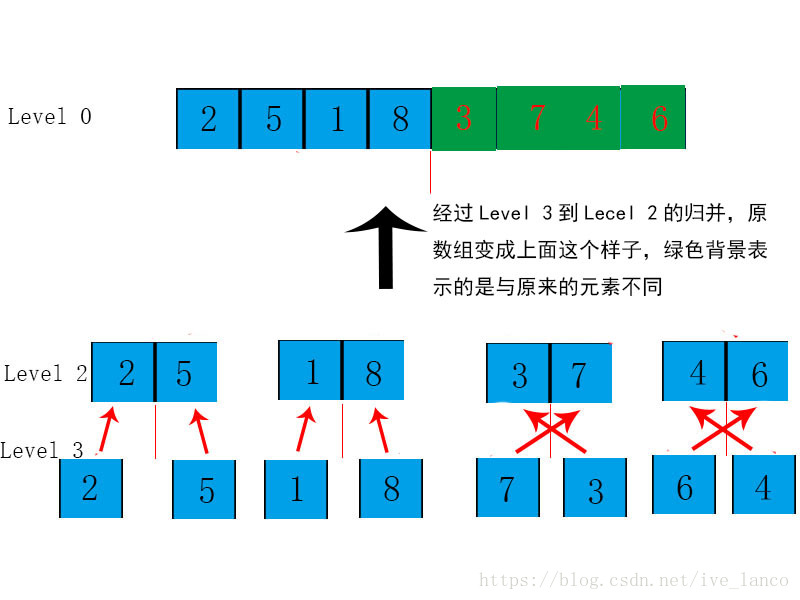
最后一层的归并：

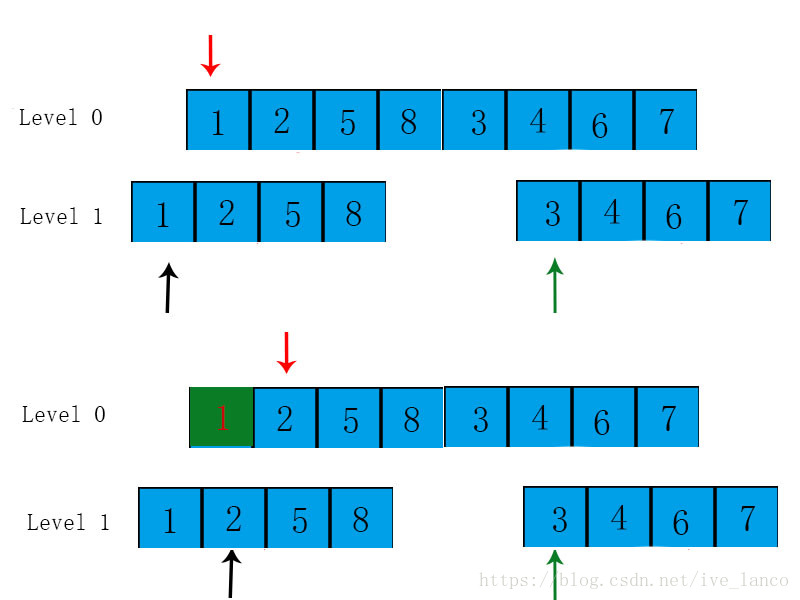
在上图中，将黑色箭头所指“1”与绿色箭头所指“2”进行大小比较，较小的赋值给箭头所指的“1”处。执行完这一步之后，红色箭头后移一个（到上图中的“2”），而将黑色箭头后移（指向途中的“2”，绿色箭头不动）当红色箭头指向元素组中第四个时（此时绿色箭头应该指向“8”，黑色箭头指向“3”）此时绿色箭头所指“3”小于黑色箭头所指“8”所以红色箭头所指的第四个元素应该被绿色箭头所指的“3”赋值掉，然后红色箭头后移一个（指向原数组第五个“3”）绿色箭头后移一个（指向“4”）而黑色的不动。一直进行这样的操作，直到元素组排好序。

自顶向下的归并排序中归并结果的轨迹如下图：

C++代码实现：

// 将arr[left...mid]和arr[mid+1...right]两部分进行归并
void __merge(int arr[], int left, int mid, int right) {
	int *temp = new int[right - left + 1];

	for (int i = left; i <= right; i++)
		temp[i - left] = arr[i];
	
	int i = left, j = mid + 1;
	for (int k = left; k <= right; k++)
	{
		if (i > mid)//左半部分的元素全部处理完
			arr[k] = temp[j++ - left];


		else if (j > right)//右半部分的元素全部处理完
			arr[k] = temp[i++ - left];

		//两边都没处理完，比较那边的元素更小
		else if (temp[i - left] < temp[j - left])
			arr[k] = temp[i++ - left];
		else
			arr[k] = temp[j++ - left];
	}
	delete[] temp;
}
//对arr[left.....right]的范围进行排序
void __mergeSort(int arr[], int left, int right) {

	if (left >= right)	
		return;
	int mid = (left + right) / 2;

	__mergeSort(arr, left, mid);
	__mergeSort(arr, mid + 1, right);
	if (arr[mid] > arr[mid+1])
		__merge(arr, left, mid, right);
}
//归并排序要调用的函数
void mergeSort(int arr[], int n) {

	__mergeSort(arr, 0, n - 1);
}