KALMAN滤波器入门总结

最新推荐文章于 2025-03-13 18:14:11 发布

iteye_6236

最新推荐文章于 2025-03-13 18:14:11 发布

阅读量171

点赞数

文章标签： matlab

本文介绍KALMAN滤波器的基本原理及其在时域信号处理中的应用。通过一个物体运动的例子，详细展示了如何使用KALMAN滤波器来估计物体的位置与速度，并用MATLAB进行了仿真验证。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

课上提到了KALMAN滤波器，稍微入个门，总算懂了点皮毛，总结了一下，如有错误欢迎指正

参考资料http://www.innovatia.com/software/papers/kalman.htm

不同于FIR、IIR经典频域滤波器，KALMAN滤波器是时域滤波器，是通过时域上的包含噪声的测量数据，计算出最接近实际值的方法

几个关键公式如下

预测

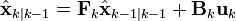
$\hat{\textbf{x}}_{k|k-1} = \textbf{F}_{k}\hat{\textbf{x}}_{k-1|k-1} + \textbf{B}_{k} \textbf{u}_{k}$

$\textbf{P}_{k|k-1} = \textbf{F}_{k} \textbf{P}_{k-1|k-1} \textbf{F}_{k}^{\text{T}} + \textbf{Q}_{k}$

更新

$\textbf{S}_k = \textbf{H}_k \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} + \textbf{R}_k$

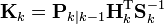
$\textbf{K}_k = \textbf{P}_{k|k-1}\textbf{H}_k^\text{T}\textbf{S}_k^{-1}$

$\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_k) \textbf{P}_{k|k-1}$

$\tilde{\textbf{y}}_k = \textbf{z}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1}$

$\hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_k$

1、假设

考虑在无摩擦无限长轨道上的一个物体静止在0点

受到风的随机扰动从而产生加速度a_k （假设符合均值为0，标准差为σ_a的正态分布），即过程噪声。

每隔Δt时间测量一次位置，但该测量并不精确，存在随机测量误差，即测量噪声。

现在我们用KALMAN滤波器来推测该物体的位置与速度

2、真实状态

$\textbf{x}_{k} = \begin{bmatrix} x \\ \dot{x} \end{bmatrix}$

状态空间：位置与速度 $\dot{x}$

根据牛顿定律k时刻与k+1时刻有如下关系

$\textbf{x}_{k} = \textbf{F} \textbf{x}_{k-1} + \textbf{G}a_{k}$

$\textbf{F} = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix}$

$\textbf{G} = \begin{bmatrix} \frac{\Delta t^{2}}{2} \\ \Delta t \end{bmatrix}$

化简一下

$\textbf{x}_{k} = \textbf{F} \textbf{x}_{k-1} + \textbf{w}_{k}$

其中

$\textbf{w}_{k} \sim N(0, \textbf{Q})$

且

$\textbf{Q}=\textbf{G}\textbf{G}^{\text{T}}\sigma_a^2 =\begin{bmatrix} \frac{\Delta t^4}{4} & \frac{\Delta t^3}{2} \\ \frac{\Delta t^3}{2} & \Delta t^2 \end{bmatrix}\sigma_a^2.$

3、测量

测量时存在噪声误差 v_k ，且符合均值为0标准差为σ_z的正态分布

$\textbf{z}_{k} = \textbf{H x}_{k} + \textbf{v}_{k}$

其中

$\textbf{H} = \begin{bmatrix} 1 & 0 \end{bmatrix}$

4、根据测量与估计判断实际状态

核心部分

1、计算Innovation

$\tilde{\textbf{y}}_k = \textbf{z}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1}$

2、计算Innovation的标准差矩阵

$\textbf{S}_k = \textbf{H}_k \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} + \textbf{R}_k$

3、计算 Kalman gain

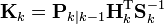
$\textbf{K}_k = \textbf{P}_{k|k-1}\textbf{H}_k^\text{T}\textbf{S}_k^{-1}$

4、计算估计值

$\hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_k$

5、更新矩阵给下次计算

$\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_k) \textbf{P}_{k|k-1}$

用MATLAB仿真了一下

dt=0.1,duration=20, measnoise = 10; accelnoise = 1.5;

%http://blog.youkuaiyun.com/boksic
F = [1 dt; 0 1]; % transition matrix
H = [1 0]; % 测量矩阵
xk = [0; 0]; %初始状态，位置速度都为0
xhat = xk; % 初始估计值

Q = accelnoise^2 * [dt^4/4 dt^3/2; dt^3/2 dt^2]; % process noise covariance
P = Q; % initial estimation covariance
R = measnoise^2; % measurement error covariance

% set up the size of the innovations vector
Inn = zeros(size(R));

pos = []; % true position array
poshat = []; % estimated position array
posmeas = []; % measured position array

Counter = 0;
for t = 0 : dt: duration,
    Counter = Counter + 1;
    %产生过程噪声
    ProcessNoise = accelnoise * randn * [(dt^2/2); dt];
    %模拟产生真实状态X
    xk = F * xk + ProcessNoise;
    %测量噪声
    MeasNoise = measnoise * randn;
    %模拟测量结果
   zk = H * xk + MeasNoise;

    % 以下为滤波

    % Innovation，测量值与估计值的差
    Inn = zk - H * xhat;
    % Covariance of Innovation
    s = H * P * H' + R;
    % Gain matrix，可看做根据测量值与估计值的可信度得到的权重系数
    K = a * P * H' * inv(s);
    % 计算最优估计值

    %F*xhat为根据牛顿定律推算当前值

    %K*Inn为修正项

    xhat = F * xhat + K * Inn;
    % 更新标准差矩阵，从而不断的循环
    P = F * P * F' + Q - F * P * H' * inv(s) * H * P * F';
    pos = [pos; xk(1)];
    posmeas = [posmeas; zk];
    poshat = [poshat; xhat(1)];
end

%显示结果
t = 0 : dt : duration;
t = t';
plot(t,pos,'r',t,poshat,'g',t,posmeas,'b');
grid;
xlabel('时间 (sec)');
ylabel('位置 (feet)');
title('Kalman Filter Performance');
legend('真实值','预测值','测量值')