开开心心学算法--快速排序之会场安排问题-优快云博客

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

步骤为：

从数列中挑出一个元素，称为 "基准"（pivot），
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

快速排序是二叉查找树（二叉查找树）的一个空间优化版本。不以循序地把项目插入到一个明确的树中，而是由快速排序组织这些项目到一个由递归调用所意含的树中。这两个算法完全地产生相同的比较次数，但是顺序不同。

从一开始快速排序平均需要花费O(nlogn)时间的描述并不明显。但是不难观察到的是分区运算，数组的元素都会在每次循环中走访过一次，使用O(n)的时间。在使用结合（concatenation）的版本中，这项运算也是O(n)。

在最好的情况，每次我们运行一次分区，我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此，在到达大小为一的数列前，我们只要作 logn次嵌套的调用。这个意思就是调用树的深度是O(logn)。但是在同一层次结构的两个程序调用中，不会处理到原来数列的相同部份；因此，程序调用的每一层次结构总共全部仅需要O(n)的时间（每个调用有某些共同的额外耗费，但是因为在每一层次结构仅仅只有O(n)个调用，这些被归纳在O(n)系数中）。结果是这个算法仅需使用O(nlogn)时间。

另外一个方法是为T(n)设立一个递归关系式，也就是需要排序大小为n的数列所需要的时间。在最好的情况下，因为一个单独的快速排序调用牵涉了O(n)的工作，加上对n/2大小之数列的两个递归调用，这个关系式可以是：

T( n) = O( n) + 2T( n/2)

解决这种关系式型态的标准数学归纳法技巧告诉我们T(n) = O(nlogn)。

事实上，并不需要把数列如此精确地分区；即使如果每个基准值将元素分开为 99% 在一边和 1% 在另一边，调用的深度仍然限制在 100logn，所以全部运行时间依然是O(nlogn)。

然而，在最坏的情况是，两子数列拥有大各为 1 和n-1，且调用树（call tree）变成为一个n个嵌套（nested）调用的线性连串（chain）。第i次调用作了O(n-i)的工作量，且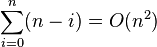 $\sum_{i=0}^n (n-i) = O(n^2)$ 递归关系式为：

T( n) = O( n) + T(1) + T( n- 1) = O( n) + T( n- 1)

这与插入排序和选择排序有相同的关系式，以及它被解为T(n) = O(n²)。

以上是理论，下面是一个实例--会场安排问题，题目如下：

描述学校的小礼堂每天都会有许多活动，有时间这些活动的计划时间会发生冲突，需要选择出一些活动进行举办。小刘的工作就是安排学校小礼堂的活动，每个时间最多安排一个活动。现在小刘有一些活动计划的时间表，他想尽可能的安排更多的活动，请问他该如何安排。

输入

第一行是一个整型数m(m<100)表示共有m组测试数据。
每组测试数据的第一行是一个整数n(1<n<10000)表示该测试数据共有n个活动。
随后的n行，每行有两个正整数Bi,Ei(0<=Bi,Ei<10000),分别表示第i个活动的起始与结束时间（Bi<=Ei)

输出

对于每一组输入，输出最多能够安排的活动数量。
每组的输出占一行

样例输入

样例输出

1
2

提示

注意：如果上一个活动在t时间结束，下一个活动最早应该在t+1时间开始

在这个题目中，对排序的要求很高，一般的如冒泡排序是通不过的，因为他的时间限制为：3000ms。下面是我的解，我选择的是快速排序算法。

#include <stdio.h>
#include <stdlib.h>

typedef struct party_time{
		int start_time;    //开始时间
		int end_time;				//结束时间
	}PARTY;
	
	//快速排序算法 参数: a[]:数组 l:左边起始点  h:右边起始点
void quicksort(PARTY a[],int l,int h)  
{
	if(l>=h)
		return;
  int j,i;
  PARTY key;
  i=l;j=h;
  key.start_time=a[i].start_time;  //给参考点赋值
  key.end_time=a[i].end_time;
  while(i<j)
    {
       while( (i<j) && ( a[j].end_time > key.end_time) )  //直到在右边找到比参考值小的
       	j--;
       if (i<j) 
       	{
       		a[i].start_time = a[j].start_time;   //将找到的值赋给左边
       		a[i++].end_time = a[j].end_time;
       	}
       while( (i<j) && ( a[i].end_time < key.end_time) )  //直到在左边找到比参考值大的
       	i++;
       if (i<j) 
       	{
       		a[j].start_time = a[i].start_time;  //将找到的值赋给右边
       		a[j--].end_time = a[i].end_time;
       	}
    }
  	a[i].start_time=key.start_time;  //将参考值移到中间
  	a[i].end_time=key.end_time;
   	quicksort(a,l,i-1); //递归调用
   	quicksort(a,i+1,h);
}

int main()
{
	int m,n,i,j;
	PARTY party_t[10000];
	scanf("%d",&m);
	while(m--)
	{
		int count =1;
		scanf("%d",&n);
		for(i=0;i<n;i++)  //输入
		{
			scanf("%d%d",&party_t[i].start_time,&party_t[i].end_time);
		}
		
		quicksort(party_t,0,n-1);  //快速排序
		i=0;
    for(j=1;j<n;j++)  //一个结束时间要小于上一个开始时间：count++
    {
        if(party_t[i].end_time<party_t[j].start_time) {i=j;count++;}
        else continue;
    }
		printf("%d\n",count);
	}
	return 1;
}