【31】共有三类药，分别重1g,2g,3g，放到若干个瓶子中，现在能确定每个瓶子中只有其中一种药，且每瓶中的药片足够多，能只称一次就知道各个瓶子中都是盛的哪类药吗？如果有4类药呢？5类呢？N类呢(N可数)？如果是共有m个瓶子盛着n类药呢(m，n为正整数，药的质量各不相同但各种药的质量已知)？你能只称一次就知道每瓶的药是什么吗？
注：当然是有代价的，称过的药我们就不用了
第一个瓶子拿出一片，第二个瓶子拿出四片，第三个拿出十六片，……第m个拿出n+1的m-1次方片。把所有这些药片放在一起称重量。
【32】假设在桌上有三个密封的盒，一个盒中有2枚银币(1银币=10便士)，一个盒中有2枚镍币(1镍币=5便士)，还有一个盒中有1枚银币和1枚镍币。这些盒子被标上10便士、 15便士和20便士，但每个标签都是错误的。允许你从一个盒中拿出1枚硬币放在盒前，看到这枚硬币，你能否说出每个盒内装的东西呢？
取出标着15便士的盒中的一个硬币，如果是银的说明这个盒是20便士的，如果是镍的说明这个盒是10便士的，再由每个盒的标签都是错误的可以推出其它两个盒里的东西。
【33】有一个大西瓜,用水果刀平整地切,总共切9刀,最多能切成多少份,最少能切成多少份?主要是过程，结果并不是最重要的
最少10，最多130
见下表，表中蓝色部分服从2为底的指数函数规律，红色部分的数值均为其左边与左上角的两个数之和。
x
0123456789x个点最多能把直线分成多少部分
12345678910x条直线最多能把平面分成多少部分
1247111622293746x个平面最多能把空间分成多少部分
12481526426493130
【34】一个巨大的圆形水池，周围布满了老鼠洞。猫追老鼠到水池边，老鼠未来得及进洞就掉入水池里。猫继续沿水池边缘企图捉住老鼠（猫不入水）。已知V猫=4V鼠。问老鼠是否有办法摆脱猫的追逐？
第一步：游到水池中心。
第二步：从水池中心游到距中心R/4处，并始终保持鼠、水池中心、猫在一直线上。
第三步：沿与中心相反方向的直线游3R/4就可以到达水池边，而猫沿圆周到达那里需要3.14R，所以捉不到老鼠。
三个阶段如下图所示：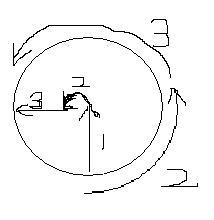
【35】有三个桶，两个大的可装8斤的水，一个小的可装3斤的水，现在有16斤水装满了两大桶就是8斤的桶，小桶空着，如何把这16斤水分给4个人，每人4斤。没有其他任何工具，4人自备容器，分出去的水不可再要回来。
表示为880，接下来，将一个大桶的水倒入小桶中，倒满，表示为853，（第2个大桶减3，小桶加3）则过程如下：
880——853：将3斤给第1个人，变为850（此时4人分别有水3-0-0-0）
850——823：将2斤给第2个人，变为803（此时4人分别有水3-2-0-0）
803——830——533——560——263——281：将1斤给第1个人，变为280（此时4人分别有水4-2-0-0）
280——253——703——730——433——460——163：将1斤给第3个人，变为063（此时4人分别有水4-2-1-0）
063——081：将1斤给第4个人，变为080（此时4人分别有水4-2-1-1）
080——053——350——323：将2斤给第2个人，将2个3斤分别给第3、4个人，（此时4人分别有水4-4-4-4）
【36】从前有一位老钟表匠，为一个教堂装一只大钟。他年老眼花，把长短针装配错了，短针走的速度反而是长针的12倍。装配的时候是上午6点，他把短针指在“6 ”上，长针指在“12”上。老钟表匠装好就回家去了。人们看这钟一会儿7点，过了不一会儿就8点了，都很奇怪，立刻去找老钟表匠。等老钟表匠赶到，已经是下午7点多钟。他掏出怀表来一对，钟准确无误，疑心人们有意捉弄他，一生气就回去了。这钟还是8点、9点地跑，人们再去找钟表匠。老钟表匠第二天早晨8点多赶来用表一对，仍旧准确无误。请你想一想，老钟表匠第一次对表的时候是7点几分？第二次对表又是8点几分？
7点x分：(7+x/60)/12=x/60 x=7*60=420/11=38.2
第一次是7点38分，第二次是8点44分
【37】今有2匹马、3头牛和4只羊，它们各自的总价都不满10000文钱（古时的货币单位）。如果2匹马加上1头牛，或者3 头牛加上1只羊，或者4只羊加上1匹马，那么它们各自的总价都正好是10000文钱了。问：马、牛、羊的单价各是多少文钱？
3600 2800 1600
【38】一天，harlan的店里来了一位顾客，挑了25元的货，顾客拿出100元，harlan没零钱找不开，就到隔壁飞白的店里把这100元换成零钱，回来给顾客找了75元零钱。过一会，飞白来找harlan，说刚才的是假钱，harlan马上给飞白换了张真钱，问harlan赔了多少钱？
100
【39】猴子爬绳这道力学怪题乍看非常简单，可是据说它却使刘易斯．卡罗尔感到困惑。至于这道怪题是否由这位因《爱丽丝漫游奇境记》而闻名的牛津大学数学专家提出来的，那就不清楚了。总之，在一个不走运的时刻，他就下述问题征询人们的意见:一根绳子穿过无摩擦力的滑轮，在其一端悬挂着一只10磅重的砝码，绳子的另一端有只猴子，同砝码正好取得平衡。当猴子开始向上爬时，砝码将如何动作呢?"真奇怪，"卡罗尔写道，"许多优秀的数学家给出了截然不同的答案。普赖斯认为砝码将向上升，而且速度越来越快。克利夫顿(还有哈考特)则认为，砝码将以与猴子一样的速度向上升起，然而桑普森却说，砝码将会向下降!"一位杰出的机械工程师说"这不会比苍蝇在绳子上爬更起作用"，而一位科学家却认为"砝码的上升或下降将取决于猴子吃苹果速度的倒数"，然而还得从中求出猴子尾巴的平方根。严肃地说，这道题目非常有趣，值得认真推敲。它很能说明趣题与力学问题之间的紧密联系。
砝码将以与猴子相同的速度上升，因为它们质量相同，受力也相同。
【40】两个空心球，大小及重量相同，但材料不同。一个是金，一个是铅。空心球表面图有相同颜色的油漆。现在要求在不破坏表面油漆的条件下用简易方法指出哪个是金的，哪个是铅的。
旋转看速度，金的密度大，质量相同，所以金球的实际体积较小，因为外半径相同，所以金球的内半径较大，所以金球的转动惯量大，在相同的外加力矩之下，金球的角加速度较小，所以转得慢。
【41】有23枚硬币在桌上，10枚正面朝上。假设别人蒙住你的眼睛，而你的手又摸不出硬币的反正面。让你用最好的方法把这些硬币分成两堆，每堆正面朝上的硬币个数相同。
分成10＋13两堆， 然后翻转10的那堆
【42】三个村庄A、B、C和三个城镇A、B、C坐落在如图所示的环形山内。由于历史原因，只有同名的村与镇之间才有来往。为方便交通，他们准备修铁路。问题是：如何在这个环形山内修三条铁路连通A村与A镇， B村与B镇，C村与C镇。而这些铁路相互不能相交。（挖山洞、修立交桥都不算，绝对是平面问题）。想出答案再想想这个题说明什么问题。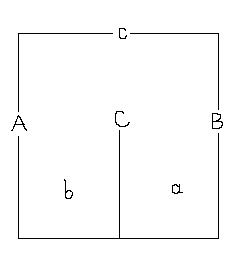
答案如右图：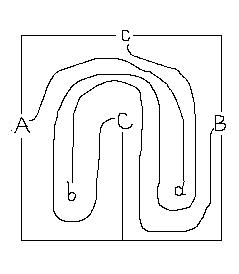
【43】屋里三盏灯泡,屋外三个开关,一个开关仅控制一盏灯,屋外看不到屋里怎样只进屋一次,就知道哪个开关控制哪盏灯?四盏呢~
温度，先开一盏，足够长时间后关了，开另一盏，进屋看，亮的为后来开的，摸起来热的为先开的，剩下的一盏也就确定了。
四盏的情况：设四个开关为ABCD，先开AB，足够长时间后关B开C，然后进屋，又热又亮为A，只热不亮为B，只亮不热为C，不亮不热为D。
【44】2+7-2+7全部有火柴根组成，移动其中任何一根，答案要求为30说明：因为书写问题作如下解释，2是由横折横三根组成，7是由横折两根组成
1, 改变赋值号.比如+,-,=
2, 注意质数.
3, 可能把画面颠倒过来.
4, 然后就可以去考虑更改其他数字更改了
247-217＝30
【45】5名海盗抢得了窖藏的100块金子，并打算瓜分这些战利品。这是一些讲民主的海盗（当然是他们自己特有的民主），他们的习惯是按下面的方式进行分配：最厉害的一名海盗提出分配方案，然后所有的海盗（包括提出方案者本人）就此方案进行表决。如果50%或更多的海盗赞同此方案，此方案就获得通过并据此分配战利品。否则提出方案的海盗将被扔到海里，然后下一名最厉害的海盗又重复上述过程。所有的海盗都乐于看到他们的一位同伙被扔进海里，不过，如果让他们选择的话，他们还是宁可得一笔现金。他们当然也不愿意自己被扔到海里。所有的海盗都是有理性的，而且知道其他的海盗也是有理性的。此外，没有两名海盗是同等厉害的——这些海盗按照完全由上到下的等级排好了座次，并且每个人都清楚自己和其他所有人的等级。这些金块不能再分，也不允许几名海盗共有金块，因为任何海盗都不相信他的同伙会遵守关于共享金块的安排。这是一伙每人都只为自己打算的海盗。最凶的一名海盗应当提出什么样的分配方案才能使他获得最多的金子呢？
如果轮到第四个海盗分配：100，0
轮到第三个：99，0，1
轮到第二个：98，0，1，0
轮到第一个：97，0，1，0，2，这就是第一个海盗的最佳方案。 
[46】他们中谁的存活机率最大？
5个囚犯，分别按1-5号在装有100颗绿豆的麻袋抓绿豆，规定每人至少抓一颗，而抓得最多和最少的人将被处死，而且，他们之间不能交流，但在抓的时候，可以摸出剩下的豆子数。问他们中谁的存活几率最大？提示：
1，他们都是很聪明的人
2，他们的原则是先求保命，再去多杀人
3，100颗不必都分完
4，若有重复的情况，则也算最大或最小，一并处死
第一个人选择17时最优的。它有先动优势。他确实有可能被逼死，后面的2、3、4号也想把1号逼死，但做不到（起码确定性逼死做不到）
可以看一下，如果第1个人选择21，他的信息时暴露给第2个人的，那么，1号就将自己暴露在一个非常不利的环境下，2-4号就会选择20，五号就会被迫在1-19中选择，则1、5号处死。所以1号不会这样做，会选择一个更小的数。
1号选择一个<20的数后，2号没有动力选择一个偏离很大的数（因为这个游戏偏离大会死），只会选择+1或-1，取决于那个死的概率小一些，再考虑这些的时候，又必须逆向考虑，1号必须考虑2-4号的选择，2号必须考虑3、4号的选择，... ...只有5号没得选择，因为前面是只有连着的两个数（且表示为N，N+1），所以5号必死，他也非常明白这一点，会随机选择一个数，来决定整个游戏的命运，但决定不了他自己的命运。
下面决定的就是1号会选择一个什么数，他仍然不会选择一个太大或太小的数，因为那样仍然是自己处于不利的地位（2-4号肯定不会留情面的），100/6=16.7（为什么除以6？因为5号会随机选择一个数，对1号来说要尽可能的靠近中央，2-4好也是如此，而且正因为2-4号如此，1号才如此... ...），最终必然是在16、17种选择的问题。
对16、17进行概率的计算之后，就得出了3个人选择17，第四个人选择16时，为均衡的状态，第4号虽然选择16不及前三个人选择17生存的机会大，但是若选择17则整个游戏的人必死（包括他自己）！第3号没有动力选择16，因为计算概率可知生存机会不如17。
所以选择为17、17、17、16、X（1-33随机），1-3号生存机会最大。
【47】有5只猴子在海边发现 一堆桃子,决定第二天来平分.第二天清晨,第一只猴子最早来到,它左分右分分不开,就朝海里扔了一只,恰好可以分成5份,它拿上自己的一份走了.第 2,3,4,5只猴子也遇到同样的问题,采用了同样的方法,都是扔掉一只后,恰好可以分成5份.问这堆桃子至少有多少只？
这堆桃子至少有3121只。
第一只猴子扔掉1个，拿走624个，余2496个；
第二只猴子扔掉1个，拿走499个，余1996个；
第三只猴子扔掉1个，拿走399个，余1596个；
第四只猴子扔掉1个，拿走319个，余1276个；
第五只猴子扔掉1个，拿走255个，余4堆，每堆255个。
如果不考虑正负，-4为一解
考虑到要5个猴子分，假设分n次。
则题目的解: 5^n-4
本题为5^5-4=3121.
设共a个桃，剩下b个桃，则b=(4/5)((4/5)((4/5)((4/5)((4/5)(a-1)-1)-1)-1)-1)-1)，即b=（1024a-8404）/3125 ; a=3b+8+53*(b+4)/1024，而53跟1024不可约，则令b=1020可有最小解，得a=3121 ,设桃数x,得方程
4/5{4/5{4/5[4/5(x-1)-1]-1}-1}=5n
展开得
256x=3125n+2101
故x=(3125n+2101)/256=12n+8+53*(n+1)/256
因为53与256不可约,所以判断n=255有一解.x为整数,等于3121
【48】话说某天一艘海盗船被天下砸下来的一头牛给击中了,5个倒霉的家伙只好逃难到一个孤岛,发现岛上孤零零的,幸好有有棵椰子树,还有一只猴子!大家把椰子全部采摘下来放在一起,但是天已经很晚了,所以就睡觉先.
晚上某个家伙悄悄的起床,悄悄的将椰子分成5份,结果发现多一个椰子,顺手就给了幸运的猴子,然后又悄悄的藏了一份,然后把剩下的椰子混在一起放回原处,最后还是悄悄滴回去睡觉了.
过了会儿,另一个家伙也悄悄的起床,悄悄的将剩下的椰子分成5份,结果发现多一个椰子,顺手就又给了幸运的猴子,然后又悄悄滴藏了一份,把剩下的椰子混在一起放回原处,最后还是悄悄滴回去睡觉了.
又过了一会 ......
又过了一会 ...
总之5个家伙都起床过,都做了一样的事情。早上大家都起床,各自心怀鬼胎的分椰子了,这个猴子还真不是一般的幸运,因为这次把椰子分成5分后居然还是多一个椰子,只好又给它了.问题来了,这堆椰子最少有多少个?
这堆椰子最少有15621
第一个人给了猴子1个，藏了3124个，还剩12496个；
第二个人给了猴子1个，藏了2499个，还剩9996个；
第三个人给了猴子1个，藏了1999个，还剩7996个；
第四个人给了猴子1个，藏了1599个，还剩6396个；
第五个人给了猴子1个，藏了1279个，还剩5116个；
最后大家一起分成5份，每份1023个，多1个，给了猴子。
【49】小明和小强都是张老师的学生，张老师的生日是M月N日，2人都知道张老师的生日是下列10组中的一天，张老师把M值告诉了小明，把N值告诉了小强，张老师问他们知道他的生日是那一天吗？
3月4日 3月5日 3月8日
6月4日 6月7日
9月1日 9月5日
12月1日 12月2日 12月8日
小明说：如果我不知道的话，小强肯定也不知道
小强说：本来我也不知道，但是现在我知道了
小明说：哦，那我也知道了
请根据以上对话推断出张老师的生日是哪一天
9.1
【50】一逻辑学家误入某部落，被囚于牢狱，酋长欲意放行，他对逻辑学家说：“今有两门，一为自由，一为死亡，你可任意开启一门。现从两个战士中选择一人负责解答你所提的任何一个问 题（Y/N），其中一个天性诚实，一人说谎成性，今后生死任你选择。”逻辑学家沉思片刻，即向一战士发问，然后开门从容离去。逻辑学家应如何发问？
问：如果我问另一个人死亡之门在哪里，他会怎么回答？
最终得到的回答肯定是指向自由之门的。
【51】说从前啊,有一个富 人,他有30个孩子,其中15个是已故的前妻所生,其余15个是继室所生,这后一个妇人很想让她自己所生的最年长的儿子继承财产,于是,有一天,他就向他 说:"亲爱的丈夫啊,你就要老了,我们应该定下来谁将是你的继承人,让我们把我们的30个孩子排成一个圆圈,从他们中的一个数起,每逢到10就让那个孩子 站出去,直到最后剩下哪个孩子,哪个孩子就继承你的财产吧!"富人一想,我靠,这个题意相当有内涵了,不错,仿佛很公平,就这么办吧~不过,当剔选过程不 断进行下去的时候,这个富人傻眼了,他发现前14个被剔除的孩子都是前妻生的,而且下一个要被剔除的还是前妻生的,富人马上大手一挥,停,现在从这个孩子 倒回去数, 继室,就是这个歹毒的后妈一想,倒数就倒数,我15个儿子还斗不过你一个啊~她立即同意了富人的动议,你猜,到底谁做了继承人呢~
老婆的儿子
【52】“有一牧场，已知养牛27头，6天把草吃尽；养牛23头，9天把草吃尽。如果养牛21头，那么几天能把牧场上的草吃尽呢？并且牧场上的草是不断生长的。”
设牛每天吃掉x，草每天长出y，原来有牧场的草量是a
a=(27x-y)*6=(23x-y)*9
可解出y=15x,a=72x,所以a=(21x-y)*12,所以需要12天。
【53】一个商人骑一头驴要穿越1000公里长的沙漠，去卖3000根胡萝卜。已知驴一次性可驮1000根胡萝卜，但每走一公里又要吃掉一根胡萝卜。问：商人共可卖出多少胡萝卜？
商人带驴驮1000根胡萝卜，先走250公里，这时，驴已吃250根，放下500根，原地返回，又吃掉250根。商人再带驴驮1000根胡萝卜，走到250公里处，这时，驴已吃250根，再驮上原先放的500根中的250根，继续前行至500公里处，这时，驴又吃250根，放下500根，剩250根返回250公里处，在驮上250公里处剩下的250根返回原地，这时驴又吃250根。商人再带驴驮1000根胡萝卜，走到500公里处，这时，驴已吃500根，再驮上原先放的500根，走出沙漠，驴吃掉500根，还剩500根。
【54】10箱黄金，每箱100块，每块一两。有贪官，把某一箱的每块都磨去一钱。请称一次找到不足量的那个箱子
第一箱子拿1块，第二箱子拿2块， 第n箱子拿n块，然后放在一起称，看看缺了几钱，缺了n钱就说明是第n个箱子。
【55】你让工人为你工作７天，给工人的回报是一根金条。金条平分成相连的７段，你必须在每天结束时都付费，如果只许你两次把金条弄断，你如何给你的工人付费？
把金条分成1，2，4三段。第一天1，第二天2，第三天1+2……第七天1+2+4。
【56】有十瓶药，每瓶里都装有100片药（仿佛现在装一百片的少了，都是十片二十片的，不管，咱们就这么来了），其中有八瓶里的药每片重10克，另有两瓶里的药每片重9克。用一个蛮精确的小秤，只称一次，如何找出份量较轻的那两个药瓶？
等同54，但此题有一些变化，与众不同的瓶子有两个，只称一次的话，只能得到两个瓶子所缺的克数的总和，我们必须保证能从总和中唯一地得出两个瓶子的所缺数。第一个瓶可拿出1片，第二个拿2片，第三个拿3片，但第四个不能拿4片，因为如果结果缺了5克的话，你就不知道是缺了2+3还是1+4。所以第四个应拿5片，第五个应拿8片，第n个应拿a(n-1)+a(n-2)片。
【57】一个经理有三个女儿， 三个女儿的年龄加起来等于13，三个女儿的年龄乘起来等于经理自己的年龄，有一个下属已知道经理的年龄，但仍不能确定经理三个女儿的年龄，这时经理说只有，一个女儿的头发是黑的，然后这个下属就知道了经理三个女儿的年龄。请问三个女儿的年龄分别是多少？为什么？
显然3个女儿的年龄都不为0，要不爸爸就为0岁了，因此女儿的年龄都大于等于1岁。这样可以得下面的情况：1*1*11=11，1*2**10=20，1*3*9=27，1*4*8=32，1*5*7=35，{1*6*6=36}，{2*2*9=36}，2*3*8=48，2*4*7=56，2*5*6=60，3*3*7=63，3*4*6=72，3*5*5=75，4*4*5=80因为下属已知道经理的年龄，但仍不能确定经理三个女儿的年龄，说明经理是36岁（因为{1*6*6=36}，{2*2*9=36}），所以3个女儿的年龄只有2种情况，经理又说只有一个女儿的头发是黑的，说明只有一个女儿是比较大的，其他的都比较小，头发还没有长成黑色的，所以3个女儿的年龄分别为2，2，9！
【58】有三个人去住旅馆，住 三间房，每一间房$10元，于是他们一共付给老板$30，第二天，老板觉得三间房只需要$25元就够了于是叫小弟退回$5给三位客人，谁知小弟贪心,只退 回每人$1，自己偷偷拿了$2，这样一来便等于那三位客人每人各花了九元，于是三个人一共花了$27，再加上小弟独吞了不$2，总共是$29。可是当初他 们三个人一共付出$30那么还有$1呢？
应该是三个人付了9*3=27，其中2付给了小弟，25付给了老板
【59】有两位盲人，他们都各自买了两对黑袜和两对白袜，八对袜了的布质、大小完全相同，而每对袜了都有一张商标纸连着。两位盲人不小心将八对袜了混在一起。他们每人怎样才能取回黑袜和白袜各两对呢？
拆开所有的袜子，每人一个
【60】有一辆火车以每小时 15公里的速度离开洛杉矶直奔纽约，另一辆火车以每小时20公里的速度从纽约开往洛杉矶。如果有一只鸟，以30公里每小时的速度和两辆火车同时启动，从洛杉矶出发，碰到另一辆车后返回，依次在两辆火车来回飞行，直到两辆火车相遇，请问，这只小鸟飞行了多长距离？
设总距离为d，总共用时d/(15+20)，两车相遇，所以鸟飞了30*d/(15+20)=6d/7
扫一扫
832
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
