Exercise 1.37

sicp的练习题1.37需要实现递归和非递归两个版本“连分数”计算黄金分割点的算法

 

连分数的介绍在这里, 它是一个类似于这样的分数：

 

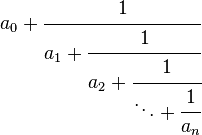
如果连分数中的[a0, a1, a2...]均取1的话，这个分式的结果就是黄金分割点的值。

 

更一般的，我们把第k层的分子叫做N_k, 分母中左侧部分叫做D_k, 那应该有一个方法：

 

cont-frac

 

这个方法有三个参数，n-gen, d-gen，它们是两个方法，参数是k，返回就是对应的k时N和D的值（对应到计算黄金分割点的公式中，这两个方法一直返回1）。第三个参数就是计算的层级，也就是k了。

 

下面是一个递归版本：

(defun cont-frac (n-gen d-gen k)
  (if (< k 2)
      (/ (funcall n-gen k)
         (funcall d-gen k))
    (/ (funcall n-gen k)
       (+ (funcall d-gen k)
          (cont-frac n-gen d-gen (- k 1))))
      )
  )

 

如果没有到最后一次迭代，就返回 N_k / (D_k + 下一次迭代的结果)

 

还有一个非递归的版本：

(defun iter-cont-frac (n-gen d-gen k)
  (defun iter-cont-frac-iter
    (n-gen d-gen k rst)
    (if (< k 1)
        rst
      (progn (format t "~a~T~a~%" rst k)
             (iter-cont-frac-iter 
              n-gen 
              d-gen
              (- k 1)
              (/ (funcall n-gen k)
                 (+ (funcall d-gen k)
                    rst)))))
    )
  (iter-cont-frac-iter n-gen d-gen k 1)
  )

 每次都使用一个额外的参数 ‘rst’来记录前面迭代的结果，这也是在递归和线性之间变换的通用方法了。

 

下面我们调用一下看看（还打印出了中间值）：

 

(format t "~a~%" (iter-cont-frac #'(lambda (i) 1.0)
                                 #'(lambda (i) 1.0)
                                 20))

 

返回的结果是这样的：

 

写道

1 20
0.5 19
0.6666667 18
0.59999997 17
0.62500006 16
0.61538464 15
0.61904765 14
0.61764706 13
0.6181818 12
0.6179775 11
0.6180556 10
0.6180257 9
0.6180371 8
0.6180328 7
0.6180344 6
0.6180338 5
0.618034 4
0.618034 3
0.618034 2
0.618034 1
0.618034