勾股定理竟然有500种证明方法，你会几种？

最新推荐文章于 2024-03-07 21:13:14 发布
转载 最新推荐文章于 2024-03-07 21:13:14 发布 · 1.7k 阅读 · 3
文章标签：

#md5 #putty #cstring #3d #d3.js

本文介绍了勾股定理的历史和发展，从商高到毕达哥拉斯，再到欧几里德和赵爽等人的证明。通过不同的几何、代数和无穷级数方法，展示了勾股定理的多样证明，如欧几里德的面积法、赵爽的‘勾股圆方图’、爱因斯坦的创新证明等。这些证明方法不仅揭示了勾股定理的数学之美，也为后续的学习和研究提供了宝贵资源。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

点击上方蓝字 关注我，涨知识

01

介绍

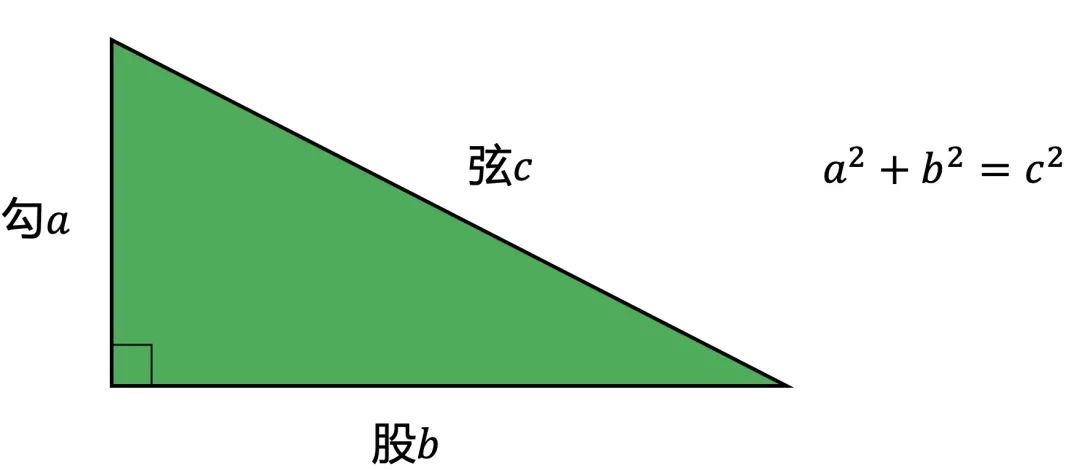
一个直角三角形，短的直角边叫勾，长的直角边叫股，斜边叫弦。勾的平方加股的平方等于弦的平方，所以称之为勾股定理。

02

商高提出

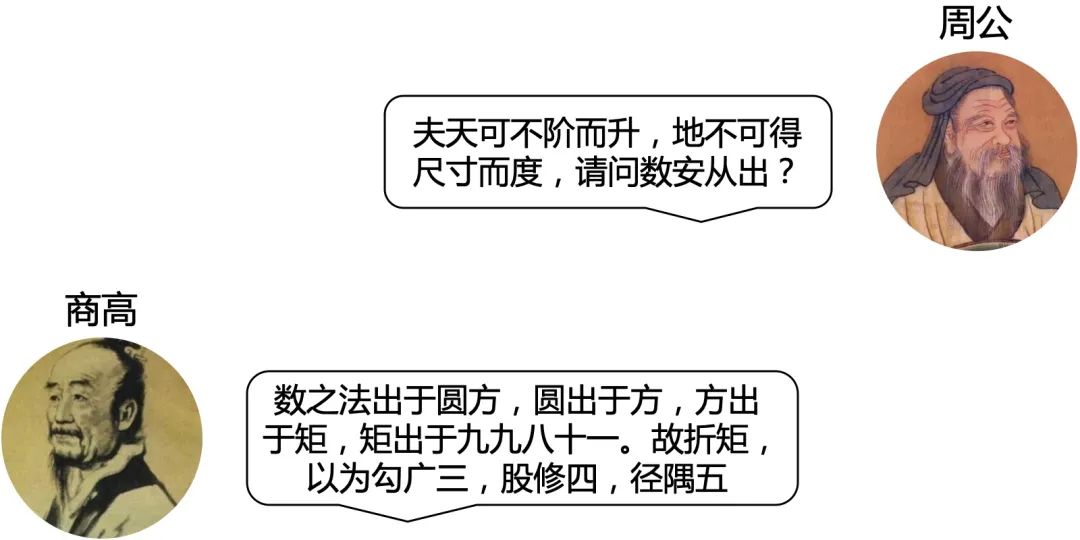
根据《周髀算经》记载，公元前1000年，商高(西周初数学家)与周公(名旦，姬昌第四子，儒学先驱)的对话中，首次提出了勾股定理。
《周髀算经》原文记载：

若求邪至日者，以日下为勾，日高为股，勾股各自乘，并而开方除之，得邪至日。

03

毕达哥拉斯提出

公元前6世纪，古希腊数学家毕达哥拉斯，提出了勾股定理，但证明方法已失传。所以西方多称这个定理为毕达哥拉斯定理。

04

欧几里德证明

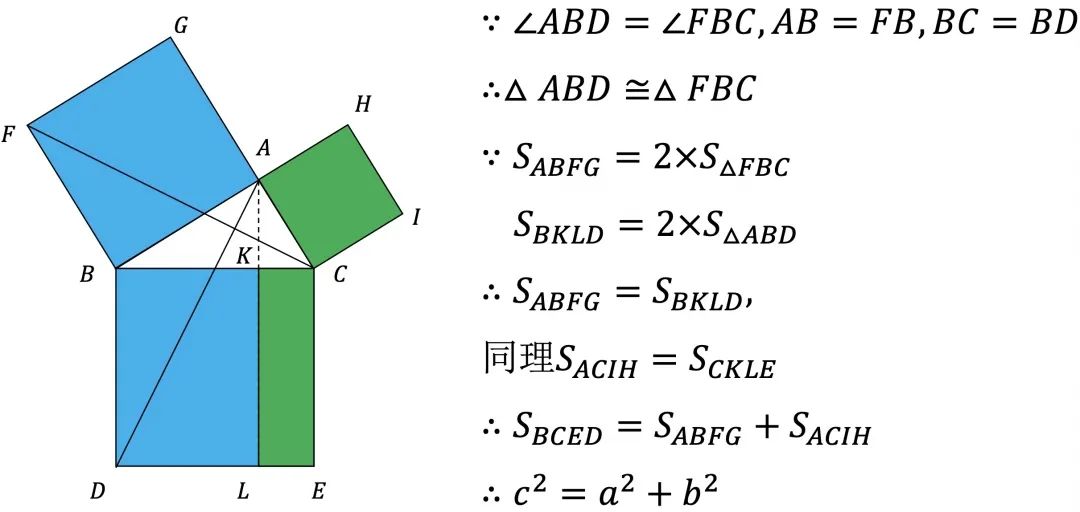
公元前4世纪，古希腊数学家欧几里德，在《几何原本》中明确证明了勾股定理。
说明：同底等高的长方形面积是三角形面积的2倍，如下同色块的面积是相等的。

05

赵爽证明

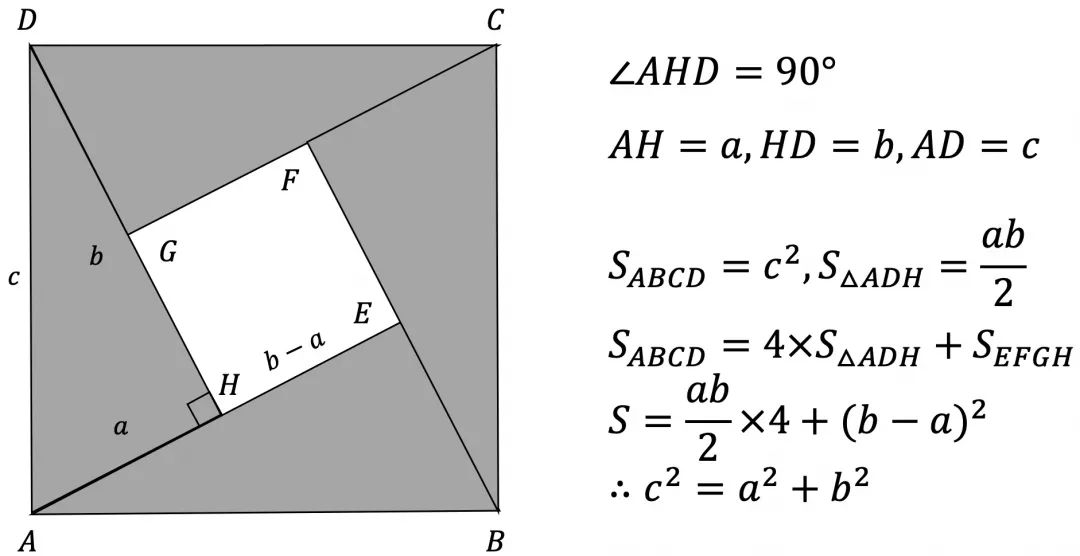
三国时期吴国数学家赵爽，在《周髀算经》的注释中记载“勾股各自乘，并之为玄实，开方除之即弦”。并通过“勾股圆方图”证明了勾股定理。
说明：大正方形的面积等于4个直角三角形加上一个小正方形面积之和。

06

爱因斯坦证明

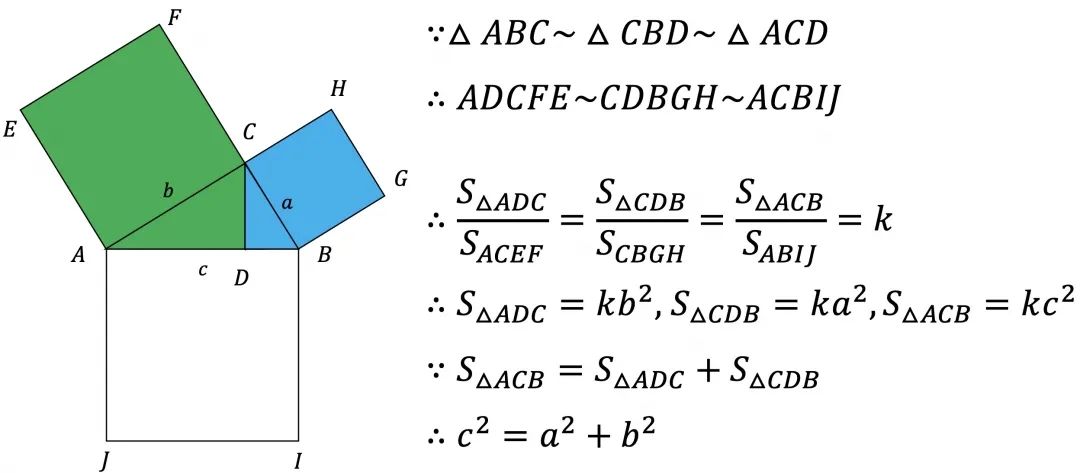
爱因斯坦在11岁时获得了一本几何书，有一天叔叔给他讲勾股定理时，他觉得证明太复杂，于是就自己想了一种方法来证明。
说明：三个直角三角形相似，那么该三角形的面积与以斜边构成的正方形面积之比固定。

07

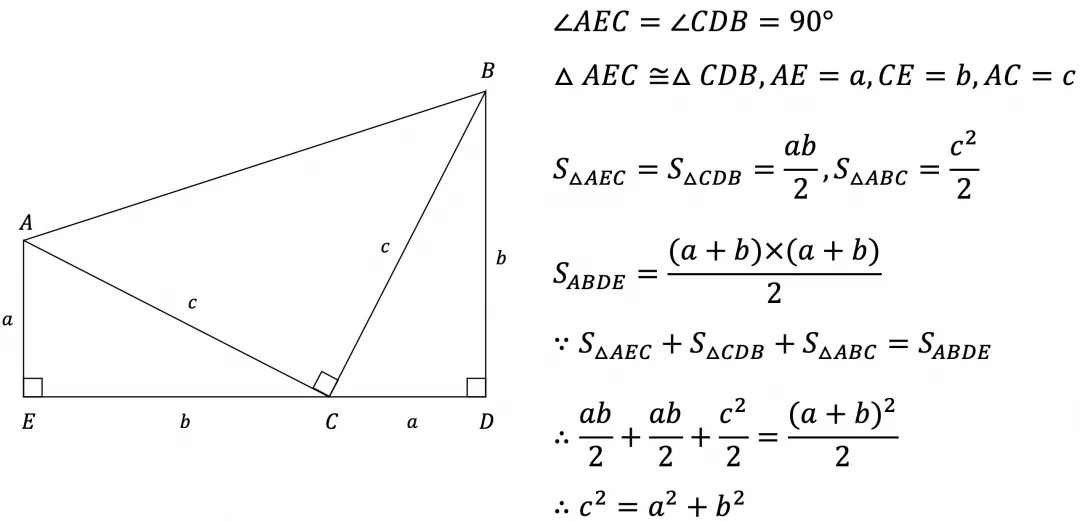
加菲尔德证明

加菲尔德在1880年当选美国第20任总统，他在五年前证明了勾股定理，因此也称这个证明方法为“总统证法”。
说明：梯形面积等于3个直角三角形的面积之和。

08

小K证明

通过相似三角形，边长之比相等，证明了勾股定理。

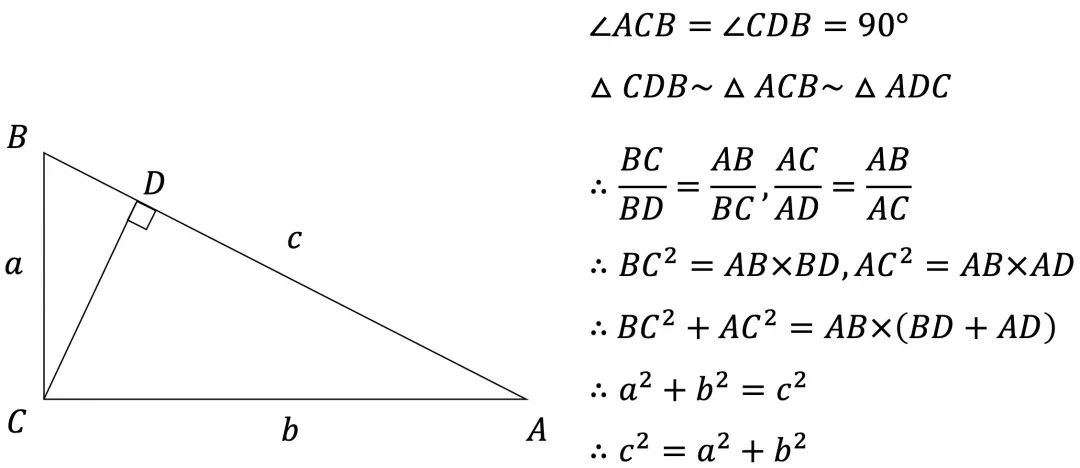
09

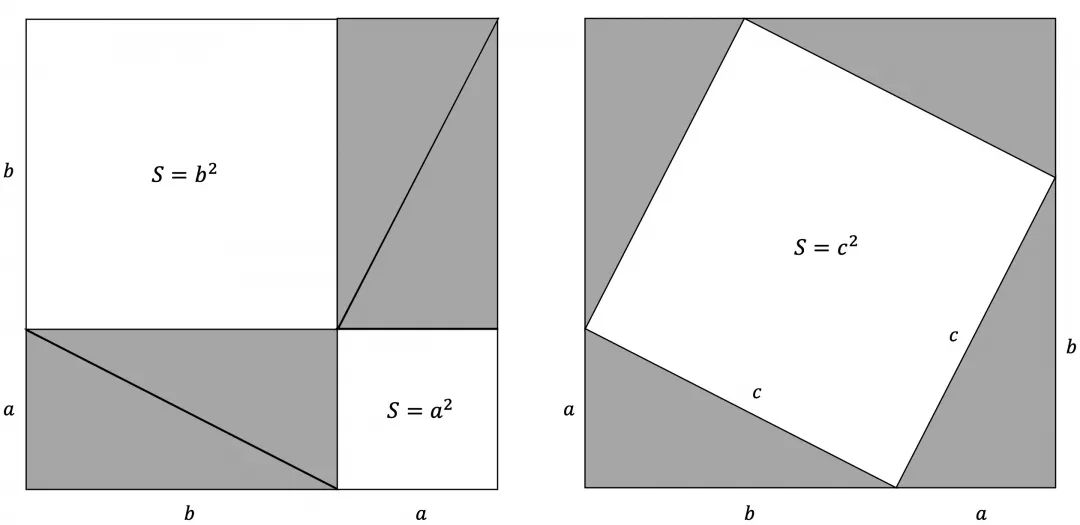
图形拼接证明

一切尽在不言中，别说话，看图。

10

辅助圆证明

以点B为圆心，BA为半径作圆，延长BC交圆于点E,D，则三角形DCA相似ACE。

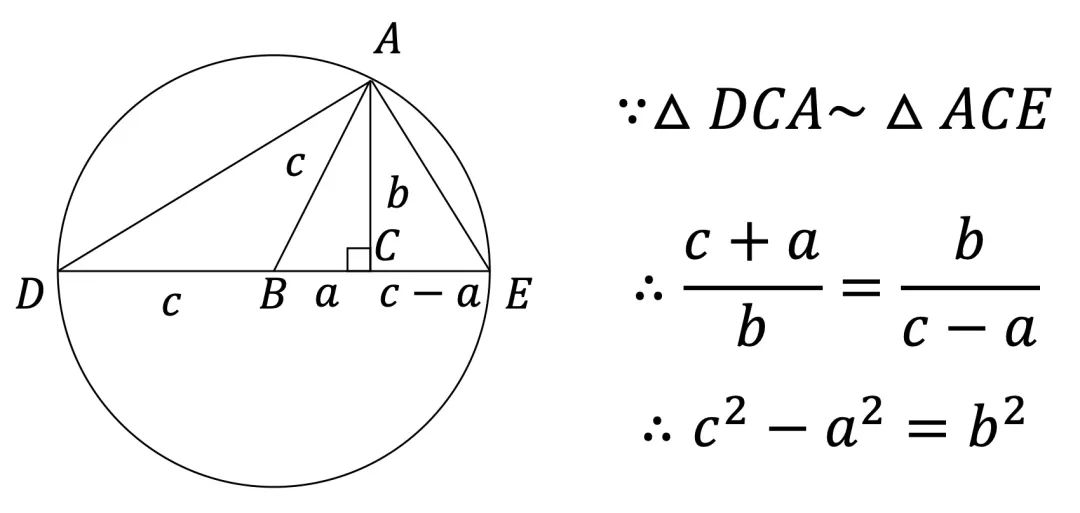
11

切割定理证明

直角三角形ABC，以点B为圆心BC为半径作圆，交AB及AB延长线于D,E，则BE=BC=BD=a。

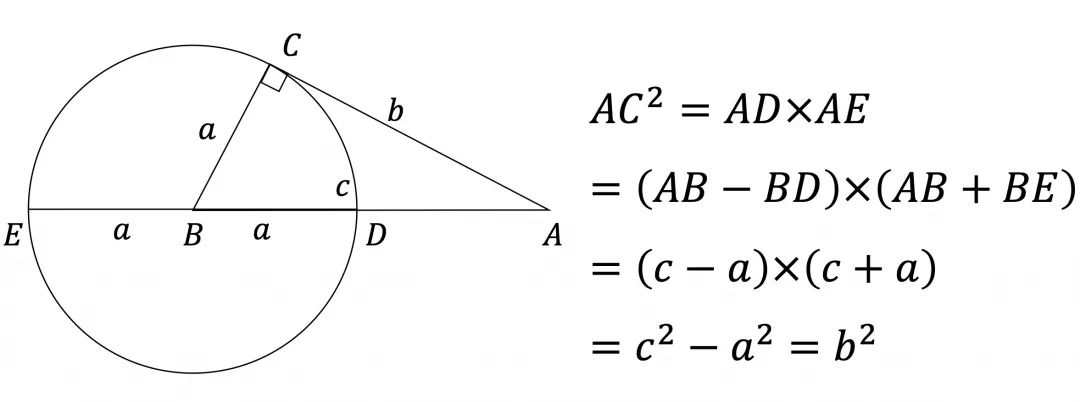
12

面积合成证明

一切尽在不言中，别说话，看图。

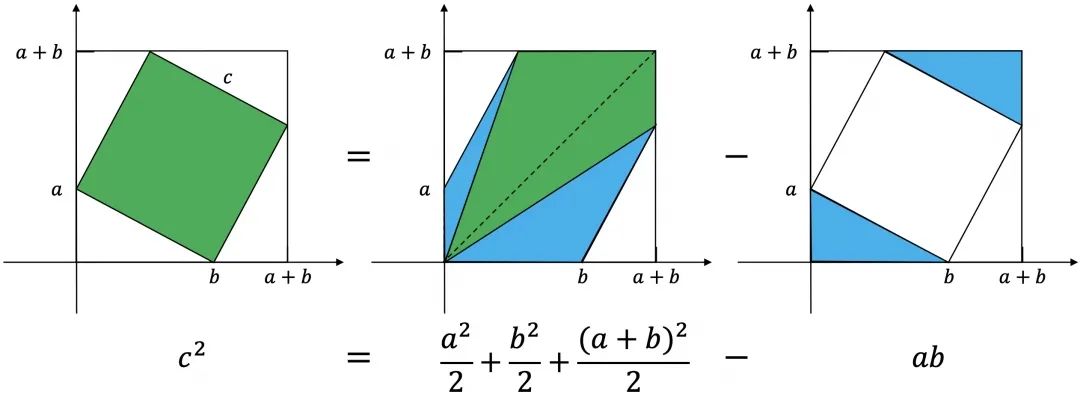
13

行列式证明

二阶行列式公式： 。

说明：二阶行列式等于以两个向量 为边张成的四边形的面积。

推广：n阶行列式就等于以n个向量为边在n维空间中张成的n维体的体积。(以后我会专门写一篇n维空间的文章)

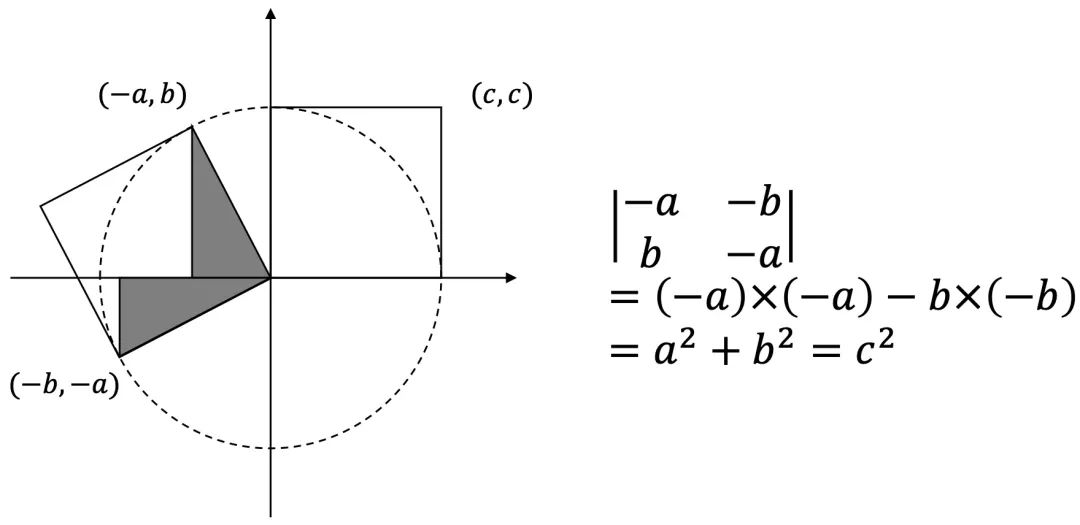
14

无穷级数证明

根据极限定理，有 。

根据如下图先得到 。

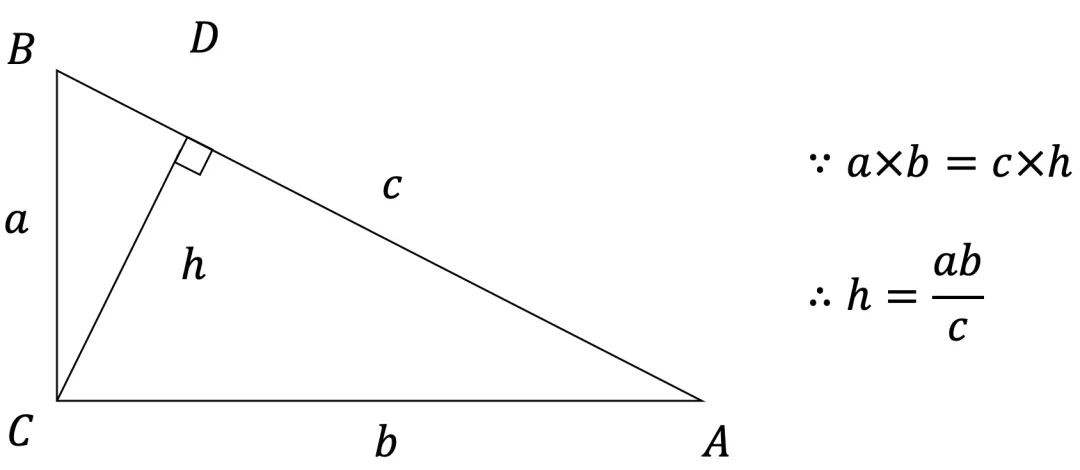
然后通过如下图的无限划分，得到 。

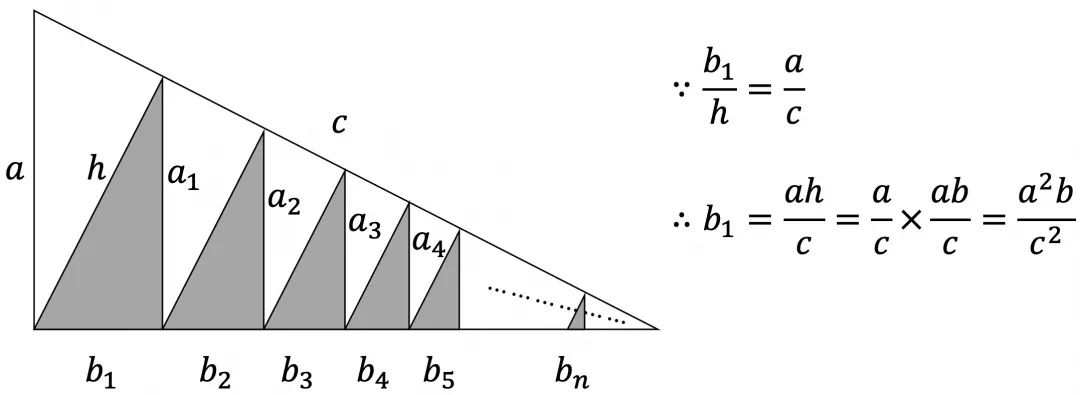
再通过如下图得到 。

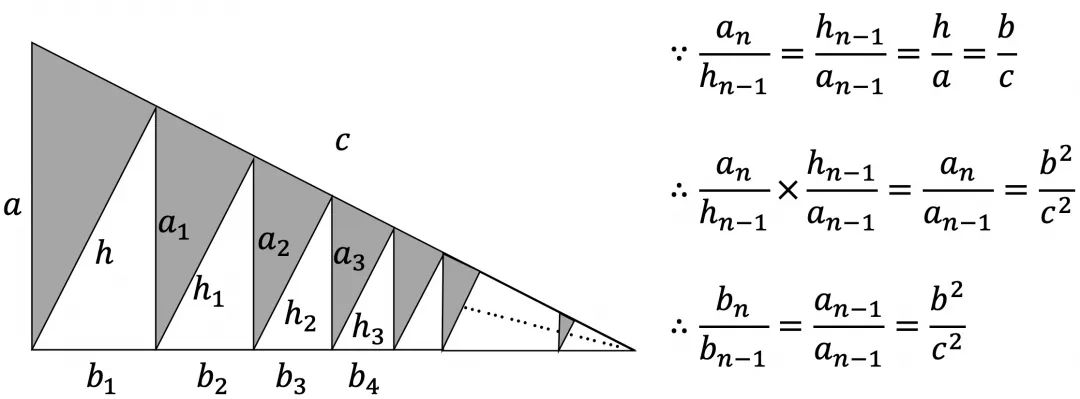
最后通过如下运算证明勾股定理。

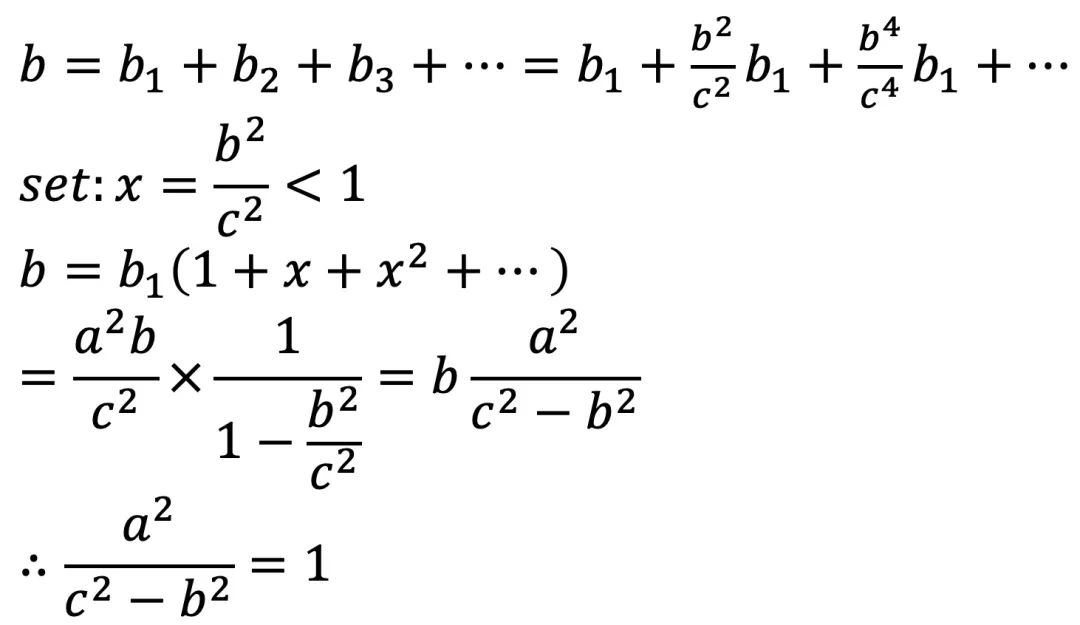
15

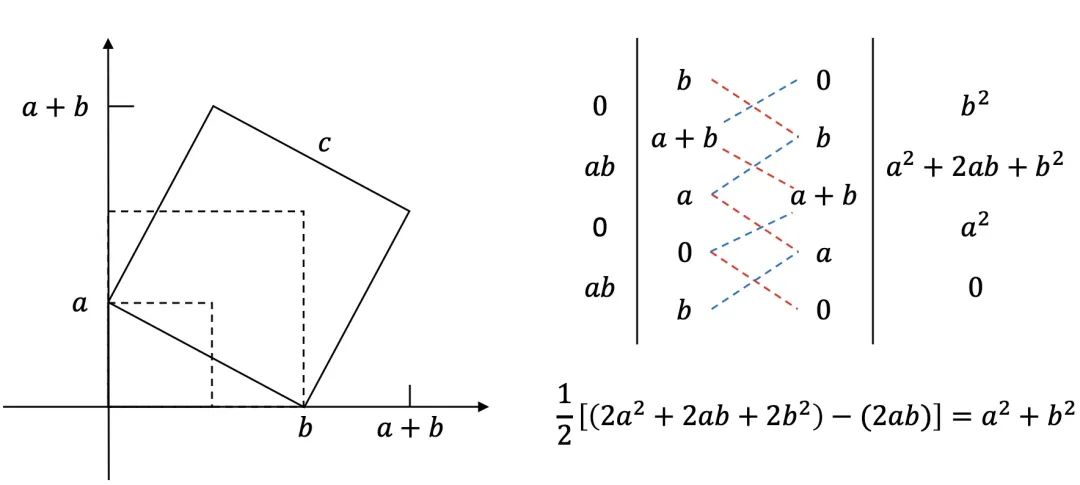
鞋带公式证明

Shoelace公式，也叫高斯面积公式，用于求多边形面积。因为计算的时候交叉相乘像系鞋带一样，所以叫鞋带公式。

由N个顶点围成的多边形，顶点分别为

，则面积为：


如果喜欢小K的文章，请点个关注，分享给更多的人，小K将持续更新，谢谢啦!

关注我，涨知识

原创不易，感谢分享

转发，点赞，在看！

▼

往期精彩回顾

▼

TCP/IP知识点及面试常考点总结

这份 Git 应急手册，关键时刻可保你一命

23 种设计模式的通俗解释，虽然有点污，但是秒懂 !

编程IT圈
关注
勾股定理几种证明方法的探索与思考毕业论文.doc
09-16
勾股定理证明方法探索与思考 本文讨论了勾股定理的几种证明方法和勾股定理的一些应用。通过对勾股定理证明方法的探索和思考，我们可以更好地理解勾股定理在数学中的地位和重要性。 1. 勾股定理的证明 勾股定理是...
勾股定理16种证明方法.doc
09-10
上述介绍的几种勾股定理的证明方法，每一种都蕴含着独特的思想和技巧。这些证明方法不仅加深了我们对勾股定理的理解，也让我们领略到数学家们的智慧和创意。在学习和研究这些证明方法的过程中，我们不仅能提高几何...
你没看错，勾股定理证明七十五种方法
杨建荣的学习笔记
02-04 1万+
勾股定理是平面几何中最重要的定理！它是历史上第一个将数与形联系起来的定理，开启了论证几何的开端，甚至引发了第一次数学危机，勾股定理的发现使人们加深了对数的理解，发现了无理数。勾股定理也是历史上第一个给出完全解答的不定方程，并引出了费马大定理。而勾股定理的证明目前约有500种，是数学定理中证明方法最多的定理之一。今天我们来分享几种证明方法，从证明方法中感受勾股定理的魅力，加深对勾股定理的理解。反正我...
勾股定理的七种经典证明
热门推荐
jjmhx的专栏
03-07 1万+
共介绍7种勾股定理的证明方法，可谓个个经典，对于初中生来说，应力求全部掌握。对数学感兴趣的朋友，也宜好好研究一下体会其中妙处。
一不小心，发现个勾股定理证明方法。
大志的博客
12-21 619
上网搜索，无意看到百度的贴 勾股定理16种证明方法https://jingyan.baidu.com/article/27fa7326e6038846f9271f46.html 挺有意思，自己也创造个方法吧。 也算是“知其然知其所以然”了。 上图 勾股定理大志证明法 如图： 任意直角三角形 ABC，三边a、b、c； 辅助： 1、作三角形的内切圆，圆心O，半径r，切点分别为...
勾股定理及其逆定理的一种简单证明方法
认知 行动 坚持
10-14 1万+
周末无聊， 图上画画， 自己的思路：
勾股定理的证明方法.doc
09-16
以下是几种不同的证明勾股定理的方法： 1. **课本证明**： 这是最基础的证明方法，通过构造8个全等的直角三角形，以及3个边长分别为a、b、c的正方形。将这些三角形和正方形拼接，可以形成两个大的正方形，它们的...
勾股定理的证明方法14746.doc
10-06
以下是基于给定文件内容的几种证明方法的详细解释： **证法1（课本证明）** 这种方法通过构造8个全等的直角三角形和3个边长分别为a、b、c的正方形。将这些三角形拼接成两个大的正方形，它们的边长都等于a+b。由于...
勾股定理思维导图+题型总结.doc
09-29
勾股定理的证明有很多种方法，其中常见的是通过图形的拼接来展示面积不变性。例如，将四个相同的直角三角形排列成一个大正方形，或者将直角三角形分割并重组，可以直观地看出面积关系，进而推导出a² + b² = c²。 ...
勾股定理最简单的证明方法
taotaobaobei的博客
09-11 1万+
在三角形中短直角边a,长直角边b,斜边c。则存在着一个公式 现在我们来证明这个勾股定理： 拿四个一模一样的三角形，通过平移，翻转拼接成右图的正方形，那么就存在面积关系+=
勾股定理 —— 证明大全
04-11 3216
a2+b2=c2 a^2+b^2=c^2 2002 年北京召开的世界数学大会，会徽如下： c2=4⋅12ab+(b−a)2⇒c2=a2+b2 c^2=4\cdot \frac12ab+(b-a)^2 ⇒ c^2=a^2+b^2 1. 不同分割方法 构造两个边长为 a+ba+b 的正方形，则采用不同的分割方法，便会有，左边白色区域的面积等于右边白色区域的面积：c2=a2+b2 c^2=a^
数论概论读书笔记 23.二次互反律的证明
Feynman1999的博客
08-27 6036
二次互反律的证明 二次互反定律有三部分。 第一部分告诉我们−1−1-1何时是二次剩余；第二部分告诉我们222何时是二次剩余。 第三部分告诉我们：（精简一下） (pq)(qp)=(−1)p−12⋅q−12(pq)(qp)=(−1)p−12⋅q−12 \left(\frac{p}{q}\right)\left(\frac{q}{p}\right)=(-1)^{\frac{p-1}{2}\cdo...
余弦定理的证明及其应用
NephrenRuqInsania
06-05 1万+
余弦定理 余弦定理，顾名思义，与余弦函数cos有关，具体的是这样的 对于任意一个三角形ABC，有如下结论 a2=b2+c2-2bc·cosA b2=a2+c2-2ac·cosB c2=a2+b2-2ab·cosC 为什么呢？ 余弦定理的证明 在上面那张图中其实大家就能看到证明方法 根据三角函数，BD=c·cosB,AD=c·sinB 那么DC=a-c·cosB 接下来，根据勾股定理，我们就可以得...
数论之费马大定理及怀尔斯的证明
weixin_30847865的博客
01-24 979
今天看到了费马大定理，初中生都知道的a^2 + b^2 = c^2(本原勾股数组有无数正整数解），费尔马推广一下，后来欧拉证明n=3，没有整数解，后来狄利克和勒让德证明5次方程无解。。。。。。，三百多年后，天才数学家怀尔斯在多人的基础上，运用现代数论与代数几何中许多深刻的结果与方法，用非常复杂的证明过程终结了费马大定理。 说白了就是：当n>=3, a^n + b^n = c^n 没有正整数...
有趣的数学证明
amcle的博客
03-20 7659
转载于：http://www.sohu.com/a/168424225_607269 “谢谢大家出席这次会议，大家能给我们数学界第一的十大最帅气证明一个面子，是我们十兄弟的荣幸，再次谢谢各位兄弟姐妹的捧场”！ “呸，我们十大最凶残公式才是数学界第一，我们曾经在英国的科学期刊《物理世界》被评为世界最伟大的十大公式，你们算啥？” “原来是喜欢砸场子的十大公式，你们虽然在数学界小有名气，可是想
用用几何画板演示赵爽弦图证明勾股定理的方法
weixin_34232363的博客
11-04 1663
在学习勾股定理的相关知识时，课本上有提到用赵爽弦图来验证该定理，在黑板上无法对图形进行动态演示，无法让学生们真正地理解。现在几何画板这一款动态课件制作工具的出现，弥补了黑板式教学的不足，下面我们就一起来看看几何画板教程是如何制作赵爽弦图证明勾股定理课件的。 中国古代的数学家们不仅很早就发现并应用勾股定理，而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的，是三国时期吴国的数学家赵爽。...
勾股定理如何证明
最新发布
07-17
<think>我们被要求证明勾股定理。勾股定理指出：在直角三角形中，直角边的平方和等于斜边的平方。即，如果直角三角形的两条直角边长度为a和b，斜边长度为c，则满足 $a^2 + b^2 = c^2$。 我们将通过几种不同的证明方法来展示，这些方法在历史上和数学教育中都是经典的。 方法一：欧几里得证明（几何法） 欧几里得在《几何原本》中给出了一个经典的证明。该证明基于几何图形的面积关系。 构造一个边长为a+b的正方形，并在其内部作四个全等的直角三角形（直角边为a、b，斜边为c），使它们围成一个边长为c的小正方形。 大正方形的面积可以表示为：$(a+b)^2 = a^2 + 2ab + b^2$。 同时，大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积：$4 \times \frac{1}{2}ab + c^2 = 2ab + c^2$。 因此有：$a^2 + 2ab + b^2 = 2ab + c^2$。 两边同时减去2ab，得到：$a^2 + b^2 = c^2$。 方法二：赵爽弦图（中国古法） 中国古代数学家赵爽利用弦图证明了勾股定理。弦图由四个全等的直角三角形（直角边分别为a、b，斜边为c）围成一个边长为c的大正方形，中间形成一个边长为b-a（假设b>a）的小正方形。 大正方形的面积可以表示为：$c^2$。 同时，大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积：$4 \times \frac{1}{2}ab + (b-a)^2 = 2ab + (b^2 - 2ab + a^2) = a^2 + b^2$。 因此：$c^2 = a^2 + b^2$。 方法三：相似三角形法（利用比例关系） 通过直角三角形斜边上的高，将原三角形分成两个小直角三角形，这两个小直角三角形都与原三角形相似。 设原三角形ABC，直角为C，斜边AB上的高为CD（D在AB上）。 则△ACD∽△ABC，△CBD∽△ABC。 由相似比例：$\frac{AD}{AC} = \frac{AC}{AB}$，即 $AC^2 = AD \cdot AB$。 同理：$\frac{BD}{BC} = \frac{BC}{AB}$，即 $BC^2 = BD \cdot AB$。 两式相加：$AC^2 + BC^2 = (AD+BD) \cdot AB = AB^2$，即 $a^2 + b^2 = c^2$。 方法四：代数法（利用恒等式） 利用代数恒等式：$(a-b)^2 + 4 \times \frac{1}{2}ab = a^2 - 2ab + b^2 + 2ab = a^2 + b^2$。 同时，这个恒等式对应的几何图形可以构造如下：四个全等的直角三角形（直角边a、b）可以拼成一个边长为c的大正方形，但中间留有一个边长为|a-b|的正方形空洞。因此，整个大正方形的面积等于四个三角形面积加上中间小正方形面积，即：$c^2 = (a-b)^2 + 4 \times \frac{1}{2}ab = a^2 - 2ab + b^2 + 2ab = a^2 + b^2$。 方法五：毕达哥拉斯证明（面积法） 毕达哥拉斯学派给出了一种证明：作两个边长为a+b的正方形，按照不同的方式划分，通过面积相等来证明。 在第一个正方形中，划分成四个直角三角形（直角边a、b）和一个边长为c的正方形。 在第二个正方形中，划分成两个边长为a和b的正方形（以及两个矩形，但矩形可以拆开成两个直角三角形）。 通过比较两个正方形面积相等，减去四个直角三角形的面积，得到剩余部分面积相等，即：第一个正方形中剩余一个边长为c的正方形，第二个正方形中剩余两个边长分别为a和b的正方形，因此有：$c^2 = a^2 + b^2$。 以上是几种经典的证明方法。实际上，勾股定理的证明方法有数百种之多，这里仅列举其中几种。 §§相关问题§§: 1. 勾股定理的逆定理如何证明？ 2. 勾股定理在非欧几何中是否成立？ 3. 勾股定理在实际生活中有哪些应用？</think>### 勾股定理的证明方法 勾股定理（$a^2 + b^2 = c^2$）的证明方法超过400种，以下是5种经典证明： #### 1. 欧几里得几何证明（面积法） 构造正方形$ABED$，以直角边$a$、$b$为边长，斜边$c$为对角线。 在$△ABC$中作高$CF$，将大正方形分割为两个矩形$ACFG$和$BCFJ$。 通过面积关系： $$S_{ABED} = S_{ACFG} + S_{BCFJ}$$ $$c^2 = a^2 + b^2$$ 核心依据：全等三角形的面积等价性。 #### 2. 赵爽弦图法（中国古代） 四个全等直角三角形（直角边$a,b$，斜边$c$）围成边长为$c$的大正方形，中间形成边长为$b-a$的小正方形。 面积恒等式： $$4 \times \frac{1}{2}ab + (b-a)^2 = c^2$$ 化简得： $$2ab + b^2 - 2ab + a^2 = c^2 \quad \Rightarrow \quad a^2 + b^2 = c^2$$ #### 3. 相似三角形法 过直角顶点作斜边高$CD$，将$△ABC$分为两个相似小三角形。 比例关系： $$\frac{AD}{AC} = \frac{AC}{AB} \quad \Rightarrow \quad b^2 = AD \cdot c$$ $$\frac{DB}{BC} = \frac{BC}{AB} \quad \Rightarrow \quad a^2 = DB \cdot c$$ 两式相加： $$a^2 + b^2 = c(AD + DB) = c^2$$ #### 4. 代数拼图法（加菲尔德证法） 两个全等直角三角形（直角边$a,b$）拼成梯形，斜边$c$构成大三角形。 梯形面积公式： $$\frac{1}{2}(a+b)(a+b) = \frac{1}{2}ab + \frac{1}{2}ab + \frac{1}{2}c^2$$ 化简： $$\frac{1}{2}(a^2 + 2ab + b^2) = ab + \frac{1}{2}c^2 \quad \Rightarrow \quad a^2 + b^2 = c^2$$ #### 5. 动态几何法（Geogebra可视化） 使用软件动态调整三角形边长，实时验证： ```python # Python示例（需安装Geogebra API） from geogebra import * gb = GeoGebra() triangle = gb.create_polygon([(0,0), (3,0), (0,4)]) # 直角边3,4 c = gb.distance(triangle[0], triangle[2]) # 斜边计算 gb.display_formula(f"$3^2 + 4^2 = {c**2:.1f}$") # 显示25.0 ``` **验证工具**： - [Geogebra在线验证](https://www.geogebra.org/geometry) - [Desmos交互模型](https://www.desmos.com/calculator/qlpfzpoqjf) ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值