​LeetCode刷题实战123：买卖股票的最佳时机 III

算法的重要性，我就不多说了吧，想去大厂，就必须要经过基础知识和业务逻辑面试+算法面试。所以，为了提高大家的算法能力，这个公众号后续每天带大家做一道算法题，题目就从LeetCode上面选 ！

今天和大家聊的问题叫做 买卖股票的最佳时机 III，我们先来看题面：

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most two transactions.

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

题意

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

样例

解题

https://blog.youkuaiyun.com/qq_17550379/article/details/83620892

有了前面两个问题的基础，我们首先想通过贪心解决这个问题。但是这个问题不行，因为有最多两比交易的限制。但是正因为如此这个问题也变得非常容易，我们可以参考第一个问题的解决思路。我们主要有这样几种状态buy1、buy2、sell1和sell2，涉及的状态方程为

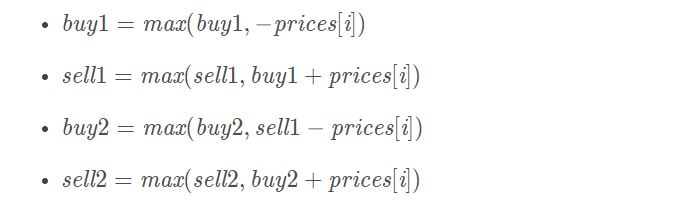
然后就是考虑边界问题，很显然buy1[0]=-prices[0]，而sell1=0（相当于买入后再卖出）、buy2-prices[0]（相当于买入后再卖出再买入）、sell2=0（相当于买入后再卖出再买入再卖出）。最后我们只要只需要返回sell2即可，因为sell2>=sell1一定成立。最后Python代码如下：

class Solution:
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        if not prices:
            return 0

        len_prices = len(prices)
        buy1, sell1, buy2, sell2 = -prices[0], 0, -prices[0], 0

        for i in range(1, len_prices):
            buy1 = max(buy1, -prices[i])
            sell1 = max(sell1, buy1 + prices[i])
            buy2 = max(buy2, sell1 - prices[i])
            sell2 = max(sell2, buy2 + prices[i])

        return sell2

好了，今天的文章就到这里，如果觉得有所收获，请顺手点个在看或者转发吧，你们的支持是我最大的动力。

上期推文：

LeetCode1-120题汇总，希望对你有点帮助！

LeetCode刷题实战121：买卖股票的最佳时机