​LeetCode刷题实战106：从中序与后序遍历序列构造二叉树

算法的重要性，我就不多说了吧，想去大厂，就必须要经过基础知识和业务逻辑面试+算法面试。所以，为了提高大家的算法能力，这个公众号后续每天带大家做一道算法题，题目就从LeetCode上面选 ！

今天和大家聊的问题叫做 从中序与后序遍历序列构造二叉树，我们先来看题面：

https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

Given inorder and postorder traversal of a tree, construct the binary tree.

Note:

You may assume that duplicates do not exist in the tree.

题意

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:

你可以假设树中没有重复的元素。

样例

解题

https://blog.youkuaiyun.com/qq_41855420/article/details/87717203

此题与上一题基本一样的解法。

中序遍历：先左子树，后根节点，再右子树
后序遍历：先左子树，后右子树，再根节点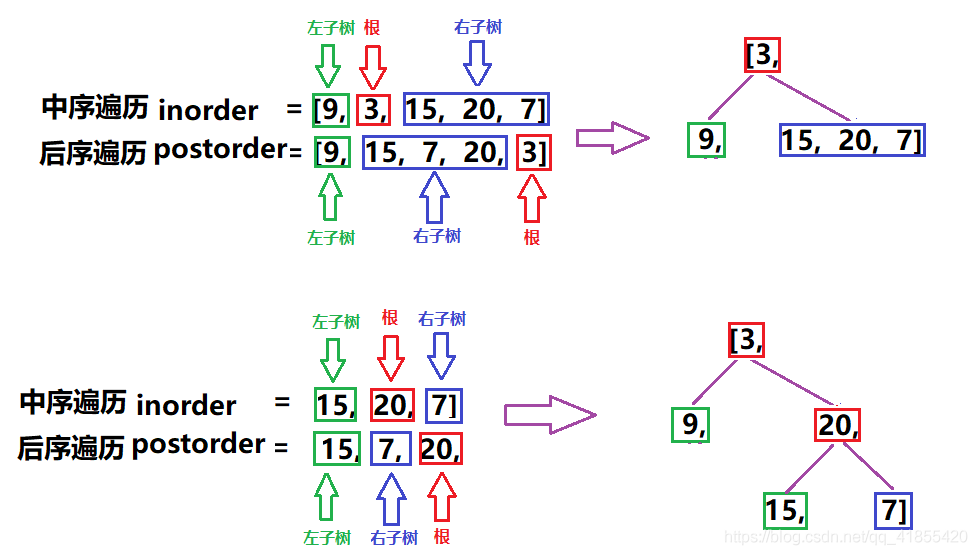

class Solution {
public:
  int orderSize;
  vector<int> inorder;//类的属性，作用类似全局遍历
  vector<int> postorder;
  //inorder [inorderBegin, inorderEnd], postorder [postorderBegin, postorderEnd] 构造成一棵树
  TreeNode* myBuildTree(int inorderBegin, int inorderEnd, int postorderBegin, int postorderEnd) {
    TreeNode *root = NULL;
    if (inorderBegin == inorderEnd) {
      root = new TreeNode(inorder[inorderBegin]);
    }
    else if (inorderBegin < inorderEnd) {
      root = new TreeNode(postorder[postorderEnd]);
      int tempValue = postorder[postorderEnd];//根节点的值，因为postorder后序遍历最后访问的根节点
      int rootIndex = inorderBegin;//根节点在inorder的下标
      while (rootIndex < inorderEnd && inorder[rootIndex] != tempValue) {//寻找根节点在inorder的下标
        ++rootIndex;
      }
      int leftCnt = rootIndex - inorderBegin;//左子树的节点个数
      root->left = myBuildTree(inorderBegin, rootIndex -1, postorderBegin, postorderBegin + leftCnt - 1);//构建左子树
      root->right = myBuildTree(rootIndex + 1, inorderEnd, postorderBegin + leftCnt, postorderEnd - 1);//构建右子树
    }
    return root;
  }
  TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    TreeNode* root = NULL;
    orderSize = inorder.size();
    int postorderSize = inorder.size();
    if (orderSize == NULL || orderSize != postorderSize) {
      return NULL;
    }
    this->inorder = inorder;//复制
    this->postorder = postorder;
    root = myBuildTree(0, orderSize - 1, 0, orderSize - 1);//构造
    return root;
  }
};

好了，今天的文章就到这里，如果觉得有所收获，请顺手点个在看或者转发吧，你们的支持是我最大的动力。

上期推文：

LeetCode1-100题汇总，希望对你有点帮助！

LeetCode刷题实战101：对称二叉树

LeetCode刷题实战102：二叉树的层序遍历

LeetCode刷题实战103：二叉树的锯齿形层次遍历

LeetCode刷题实战104：二叉树的最大深度

LeetCode刷题实战105：从前序与中序遍历序列构造二叉树