LeetCode刷题实战62：不同路径

最新推荐文章于 2025-07-16 18:49:18 发布

编程IT圈

最新推荐文章于 2025-07-16 18:49:18 发布

阅读量146

点赞数

文章标签：算法 payment 动态规划 ext 隐马尔可夫模型

算法的重要性，我就不多说了吧，想去大厂，就必须要经过基础知识和业务逻辑面试+算法面试。所以，为了提高大家的算法能力，这个公众号后续每天带大家做一道算法题，题目就从LeetCode上面选！

今天和大家聊的问题叫做 不同路径，我们先来看题面：

https://leetcode-cn.com/problems/unique-paths/

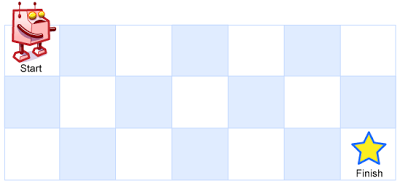
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

题意

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

样例

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

解题

https://www.cnblogs.com/techflow/p/12872847.html

解法

在我写题解的时候，我突然想起来上一次见到它好像是在某个综艺节目当中。它被作为一道智力题来考一些明星嘉宾，好像一众明星里面，只有关晓彤做了出来。。。

它作为智力题有一个标准的模板式解法：

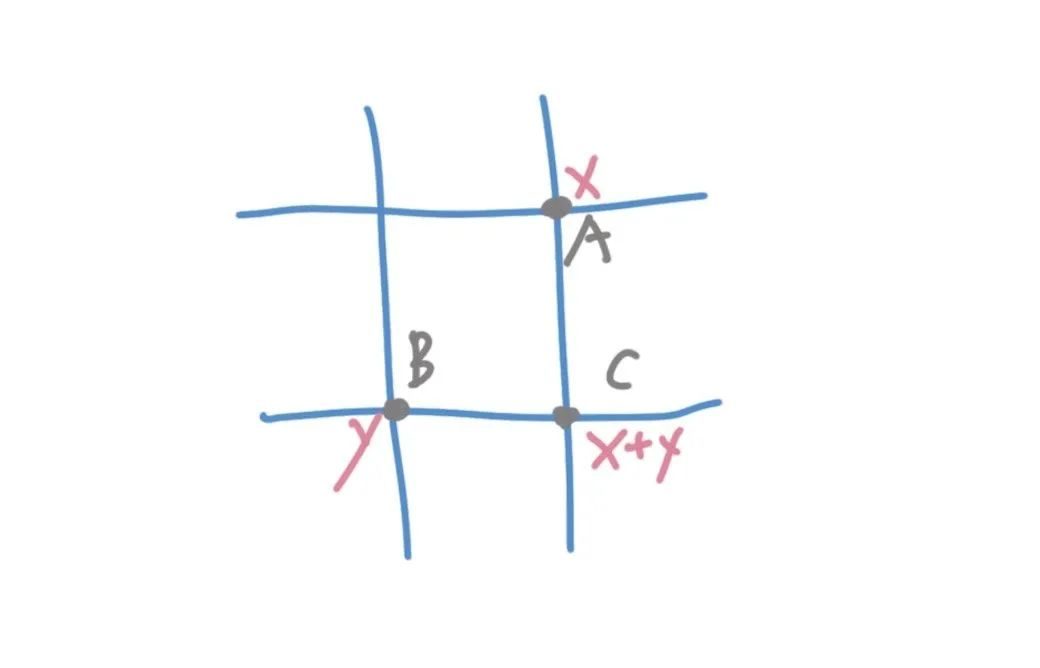
对于图中的C点来说，从起点通往它的路径数量等于通往A点和B点路径的和。

这个结论我们很多人都知道，因为C点只有两个来源，一个是A点一个是B点。它既可以从A点来，也可以从B点来，所以应该是一个加和的关系。

这当然是没错的，但不知道大家从这个过程当中有没有什么感悟。C点的上游是A点和B点，也就是说C状态是由A状态或者是B状态转移到的。这不就是一个动态规划算法吗？

我们用dp记录每一个位置的答案的话，那么可以很轻松地写出状态转移方程：

dp[i][j] = dp[i-1][j] + dp[i][j-1]

我们用代码把这个方程实现就能解出问题了。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0 for _ in range(n+2)] for _ in range(m+2)]
        
        dp[0][1] = 1
        
        for i in range(1, m+1):
            # 特殊处理第一列，因为第一列只有1种
            dp[i][1] = dp[i-1][1]
            for j in range(2, n+1):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
                
        return dp[m][n]

one more solution

如果只有上面这一种解法，那么这道题完全没有说的必要，也太简单了。这道题还有另外一种解法，会更加简单。

在上面的解法当中，我们是把这个问题当成了算法题来解决的，使用动态规划算法进行建模，适配题目来解决它。但如果我们换个思路，完全可以把它当做数学问题来解。

我们来分析一下问题，机器人要从左上角走到右下角，地图是没有缺陷的，所有点都可以到达。由于机器人没办法走回头路，也就是说机器人在通往终点的过程当中走过的路程是确定的。也就是要走n-1条横边和m-1条竖边。

边的总数和种类都确定了，其实这个问题可以转化一下。我们把走的横边看成是白球，走的竖边看成是黑球，那么这道题其实就可以转化成，我们有n-1个白球，m-1个黑球，现在把它们排成一排，一共有多少种方法？

这个是小学的组合数学问题，我们要从整体的n+m-2个物体当中，选出n-1个，那么显然答案就是：

不过，虽然我们用一个式子就表达了，但是要求解这个组合数，还是需要通过循环的。我们把它转化成:

接着我们用循环求解即可。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        ret = 1
        
        for i in range(1, n):
            ret = ret * (n+m-1-i) // i
        return ret

相比于上面的做法更加简短，虽然两者看起来都是的算法，好像差别不大。但是每个数的阶乘和组合数都是可以预处理的，在频繁求解的场景下，显然要比动态规划算法更快。