算法的重要性,我就不多说了吧,想去大厂,就必须要经过基础知识和业务逻辑面试+算法面试。所以,为了提高大家的算法能力,这个公众号后续每天带大家做一道算法题,题目就从LeetCode上面选 !
今天和大家聊的问题叫做 不同路径II,我们先来看题面:
https://leetcode-cn.com/problems/unique-paths-ii/
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
Now consider if some obstacles are added to the grids. How many unique paths would there be?
题意
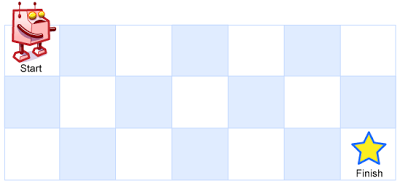
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
说明:m 和 n 的值均不超过 100。
样例
示例 1:
输入:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
解题
动态规划
我们要计算到达右下角的位置的路径数就是:走到m行、n列共有多少种走法。
利用动态规划的思想:走到m行、n列共有多少种走法用dp[m][n]表示
要到达每个位置,只能从上面来或者从左边来:dp[m-1][n]、dp[m][n-1]
要求有多少种走法就是求,到达dp[m-1][n]走法+到达dp[m][n-1]走法。即:dp[m][n]=dp[m-1][n]+dp[m][n-1]
障碍:
当遇到障碍点表示:到达这个位置的走法为0
即:dp[m][n]=0
注意:当障碍物的位置在右下角和开始位置时,是没有可达路径的。
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m=obstacleGrid.length;
int n=obstacleGrid[0].length;
if(obstacleGrid[0][0]==1 || obstacleGrid[m-1][n-1]==1){
return 0;
}
int dp[][] = new int[m + 1][n + 1];
dp[0][1]=1;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if (obstacleGrid[i - 1][j - 1] == 0)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
}
好了,今天的文章就到这里,如果觉得有所收获,请顺手点个在看或者转发吧,你们的支持是我最大的动力。
上期推文:






















 1229
1229

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










