IEEE754标准以及非常规划定义，double的二进制转换工具类

IEEE754标准

​ 今天我们要讨论的问题是在Java中：double pi = 3.14; 在内存中第10位上是0还是1？

​ 这个问题需要我们了解Java中double类型在内存中是如何存储的。那么你知道Java是如何存储double类型变量的吗？有小伙伴说“内存中当然是存二进制了！”没错，但具体是如何存储了呢？

​ 今天我们就来聊一聊Java中浮点数存储的标准，它叫IEEE754。当你看完本篇文章后，你就可以知道3.14在内存中每一位上是0还是1了。茶语饭后与同行们闲谈时，相信十人中有九人不知道啥是IEEE754，那么让我们开始吧。

我们分为如下三步骤来学习，分别是：

1、 数学中的小数十进制与二进制的转换方法

2、 小数的科学记数法格式

3、 IEEE754标准

一、数学中的小数十进制与二进制的转换方法

1.1 十进制小数转换为二进制

​ 如果你已经对小数的进制转换很熟悉了，那么可以跳过本节，直接看科学记数法格式小节。

​ 我们以(121.375)₁₀为例，把它转换成二进制。

​ 首先我们把它拆分成整数与小数两个部分，因为整数与小数的转换方式是不同的。我们先来看整数部分的转换公式。

• 整数部分转换为二进制：除以2，倒序取余

• 小数部分转换为二进制：乘以2，正序取整

所以十进制小数121.375转换为二进制为：1111001.011

小伙伴们要注意了，这只是数学层面上的转换，并不是Java内存中保存的样子。想要了解Java内存中double类型的样子必须学习IEEE754才能知道。

1.2 二进制转换为十进制

• 整数部分转十进制：按权展开求和

  例如：

  假如二进制为：0000 0001，结果就可以表示为：1 * 2º = 1
  
  假如二进制为：0000 0010，结果就可以表示为：1 * 2¹ = 2
  
  假如二进制为：0000 0100，结果就可以表示为：1 * 2² = 4
  
  所以，如果二进制为：0000 0111，结果就可以表示为：
  
     1 * 2² + 1 * 2¹ + 1 * 2º  
  
   = 4 + 2 + 1
  
   = 7
  

  针对此例，整数部分二进制：1111001，就可以表示为：

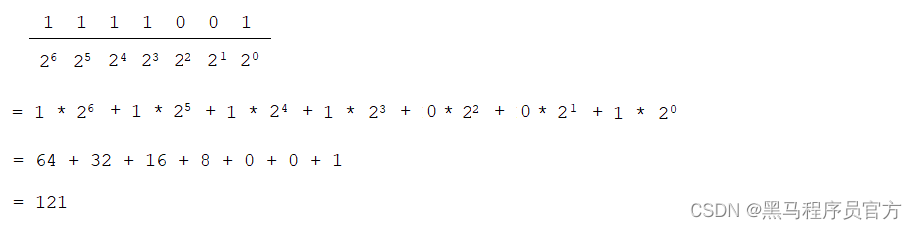
• 小数部分转十进制：按权展开求和

  针对此例，小数部分二进制：0.011，就可以表示为：

二、科学记数法

2.1 什么是科学计数法

​ 科学记数法是一种记数的方法。把一个十进制数表示成a与10的n次幂相乘的形式（1≤|a|<10，a不为分数形式，n为整数），这种记数法叫做科学记数法。

​ 例如：数字：98024.25，用科学计数法可以表示为：9.802425 * 10⁴，也可以表示为：9.802425E4

​ 数字：0.00325，用科学计数法可以表示为：3.25 * 10^-3，也可以表示为：3.25E-3

其中：

1. 其中9.8024和3.25就是a：它一定是1 ≤ |a| < 10的，也就是：a的绝对值要大于等于1，并且小于10.所以它一定是一个一位数，不能是两位数。

2. 10为底数：因为是十进制的科学计数法，所以这里是10.

3. 4和-3为指数n：它一定是个整数。

​ 使用科学计数法记数的一个好处是：在表示一个较大的数，或者较小的数时，可以节省空间和时间。

三、IEEE754标准

​ 我们已经了解了二进制与十进制之间的转换，以及小数的科学记数法。现在我们学习一下IEEE754规范中小数在是如何在内存中存储的。

3.1 64位划分成三个区

​ 通过上面的学习相信你已经了解了科学记数法了。那么IEEE754标准是怎样的呢？我们已经知道double类型是8个字节，也就是64位。其实IEEE754标准把这64位分成了三个区域，分别对应科学记数法的符号、底数、指数。只不过略有一些特殊性而已，下面我们来看一张图。

这个64位的二进制表示的浮点数到底是多少呢？我们本节都会使用这个例子来做演示。

下面先来看一个公式，然后我们通过这个公式展开讲解。

​ 浮点数＝s(±1) ×(1.f)₂ ×2^e-1023

​ 现在你可能还不能理解这个公式，不急，我们先来看二进制图。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YmGtguPL-1663670616951)(T1-IEEE754标准/1655143937684.png)]

​ 图中说明第一个区域是符号区，只有一位就是第63位。为0表示正；为1表示负。这个很好理解。上例中符号区为0，所以可以理解为s=1；当符号区为1时，可以理解为s=-1。

第二个区域是阶码区，范围是第52位到第62位，共有11位。阶码区与指数有关。

最后一个区域是尾数区，范围是第0位到第61位，共有52位。尾数区与底数有关。

我们大致了解了一下double的64位分的三个区，下面我们详细来聊一聊阶码区与尾数区。

3.1.1 符号区

符号区很好理解，它只占一位（最后一位）。通常我们用字母S来表示，如果为0表示正数，那么就是s=1；如果为1表示负数，那么就是s=-1。

3.1.2 阶码区

​ 阶码区中11位二进制范围是00000000000 ~ 11111111111，对应的十进制范围是0 ~ 4096。但它并不能表示最小指数是0最大指数是4096。因为还要表示负的指数，所以IEEE754规定阶码区的值减去1023才是最终的指数。

指数*=阶码区-1023*

当阶码区的值为1000时，再减去1023，那么最终指数就是-23了。通过这种方式就可以有负的指数了。

例如阶码区为10000000101时，那么指数等于什么呢？我们先把它转换成十进制为1029，再减去1023，结果为1029-1023=6。

s(±1)×1.f×2⁶

3.1.3 尾数区

​ 我们已经了解了符号区与阶码区，下面我们聊一聊尾数区。尾数区共52位，从第0位到第51位。我们需要在这52位的尾数前面添加“1.”就是底数了。例如尾数区为

1110010110000000000000000000000000000000000000000000，

那么底数就是：**1.**1110010110000000000000000000000000000000000000000000

IEEE754隐藏了“1.”，一定要记住这一特性，不然会计算出错的。

现在尾数区与底数之间的关系已经明白了，那么计算起来也就不难了。我们把上面二进制底数中无用的零去除：1.111001011。

让这个数乘以×2⁶，也就是(1.111001011)₂×(2⁶)₁₀，等同于把小数点向右移动6位。即：(1.111001011)₂×(2⁶)₁₀ = (1111001.011)₂

转换成十进制后的结果为：121.375

四、IEEE754中非常规化定义

​ 上面已经了解了IEEE754中规范化的定义，但IEEE754中还存在一些非规范的定义，以及本节中还要讨论为什么double类型的范围是±1.79×10³⁰⁸；double类型的非零最小绝对值是多少？为什么？

4.1 表示"零"(非常规)

​ 在I浮点数