代码随想录|day44|动态规划part06● 完全背包● 518. 零钱兑换 II ● 377. 组合总和 Ⅳ

完全背包 理论基础

视频：带你学透完全背包问题！ 和 01背包有什么差别？遍历顺序上有什么讲究？_哔哩哔哩_bilibili 

链接：代码随想录

//先遍历背包还是先遍历物品是没有影响的。可以和01背包保持一致，都先遍历物品再遍历背包，也就是一行行按行遍历。

与0、1背包不同的是，内层循环遍历背包时需要从小到大遍历，这点和0、1背包不同。

案例：

 

 完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

01背包的核心代码，01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

 

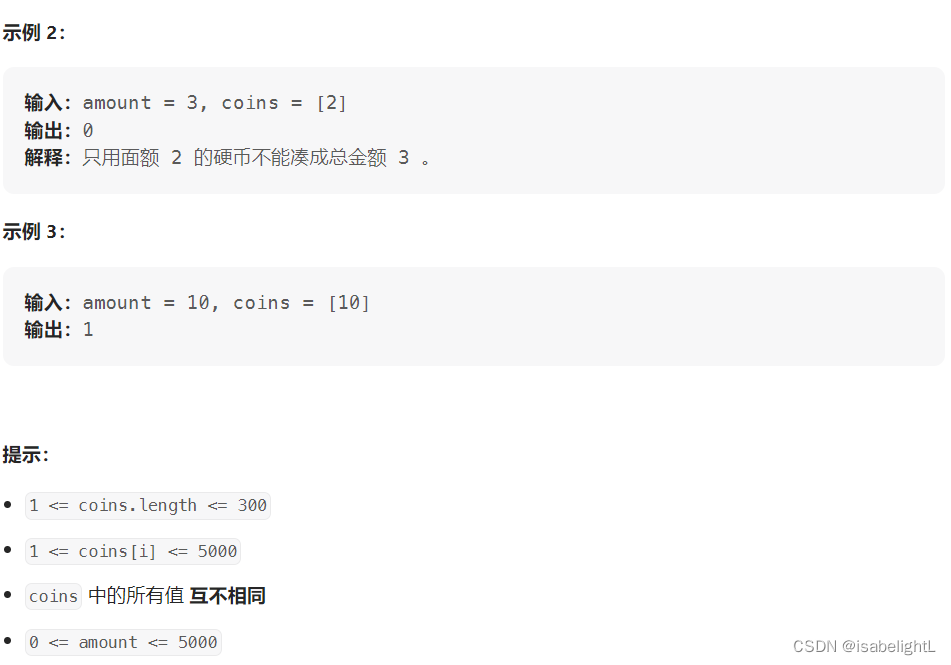
518. 零钱兑换 II

与0-1背包里目标和那道题形成联动，求得是组合数

链接：代码随想录

 

1、组合数：外层for循环遍历物品（钱币），内层for遍历背包（金钱总额）的情况：

因为每一行，比如第一行只放了物品1，物品2等到第二行才放。则当遍历dp[2]只会有（1，2），不会出现（2，1）.

for (int i = 0; i < coins.size(); i++) { // 遍历物品
    for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
        dp[j] += dp[j - coins[i]];
    }
}

2、排列数：外层for循环遍历背包（金钱总额），内层for遍历物品的情况：

背包容量的每一个值，都是经过 1 和 5 的计算，包含了{1, 5} 和 {5, 1}两种情况。

for (int j = 0; j <= amount; j++) { // 遍历背包容量
    for (int i = 0; i < coins.size(); i++) { // 遍历物品
        if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
    }
}

解法：本题是组合数，所以先背包

 

class Solution {
/*假设每一种面额的硬币有无限个。一看就是完全背包
dp[i][j] 代表只用0---i前i个硬币，且凑的总金额是j的硬币组合种数
因为问的不是最大价值，只是种类数

d[i][j]+=dp[i-1][j-coins[i]];
*/
public:
    int change(int amount, vector<int>& coins) {
        int n=coins.size();
        vector<int>dp(amount+1,0);
        //初始化必须为1，不然之后推导的都是0
        dp[0]=1;
        //vector<vector<int>>dp(n,vector<int>(amount+1,0));
        for(int i=0;i<n;i++)
        {
            for(int j=coins[i];j<=amount;j++)
            {
                dp[j]+=dp[j-coins[i]];
            }
        }
        return dp[amount];



    


    }
};

 377. 组合总和 Ⅳ

链接：代码随想录

 

 本题与前面的形成对比，是排列数。

先遍历背包容量，再遍历物品

class Solution {

public:
    int combinationSum4(vector<int>& nums, int target) {

        vector<int>dp(target+1,0);
        dp[0]=1;
        for(int j=0;j<=target;j++)//排列数，先遍历容量
        {
            for(int i=0;i<nums.size();i++)//再遍历背包
            {
                if(j-nums[i]>=0 && dp[j] < INT_MAX - dp[j- nums[i]])
                {
                    dp[j]+=dp[j-nums[i]];
                }
            }
        }
        return dp[target];
    }
};