1.连号区间数
题目
小明这些天一直在思考这样一个奇怪而有趣的问题:
在 1∼N 的某个排列中有多少个连号区间呢?
这里所说的连号区间的定义是:
如果区间 [L,R] 里的所有元素(即此排列的第 L 个到第 R 个元素)递增排序后能得到一个长度为 R−L+1 的“连续”数列,则称这个区间连号区间。
当 N 很小的时候,小明可以很快地算出答案,但是当 N 变大的时候,问题就不是那么简单了,现在小明需要你的帮助。
输入格式
第一行是一个正整数 N,表示排列的规模。
第二行是 N 个不同的数字 Pi,表示这 N 个数字的某一排列。
输出格式
输出一个整数,表示不同连号区间的数目。
数据范围
1≤N≤10000,
1≤Pi≤N
输入样例1:
4
3 2 4 1
输出样例1:
7
输入样例2:
5
3 4 2 5 1
输出样例2:
9
样例解释
第一个用例中,有 7 个连号区间分别是:[1,1],[1,2],[1,3],[1,4],[2,2],[3,3],[4,4]
第二个用例中,有 9 个连号区间分别是:[1,1],[1,2],[1,3],[1,4],[1,5],[2,2],[3,3],[4,4],[5,5]
分析
遍历左右两个端点,
代码
#include<iostream>
using namespace std;
const int N = 10010;
int a[N];
int INF = 10000000;
int main()
{
int n;
cin >> n;
for(int i = 0;i < n;i++) cin >> a[i];
int res = 0;
for(int i = 0;i < n;i++)
{
int maxv = -INF,minv = INF;
for(int j = i;j < n;j++)
{
maxv = max(maxv,a[j]);
minv = min(minv,a[j]);
if(maxv - minv == j - i) res++;
}
}
cout << res << endl;
return 0;
}
2.递增三元组
题目
给定三个整数数组
A=[A1,A2,…AN],
B=[B1,B2,…BN],
C=[C1,C2,…CN],
请你统计有多少个三元组 (i,j,k) 满足:
1≤i,j,k≤N
Ai<Bj<Ck
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,…AN。
第三行包含 N 个整数 B1,B2,…BN。
第四行包含 N 个整数 C1,C2,…CN。
输出格式
一个整数表示答案。
数据范围
1≤N≤105,
0≤Ai,Bi,Ci≤105
输入样例:
3
1 1 1
2 2 2
3 3 3
输出样例:
27
分析
算出有多少 a 比 b 小,有多少 c 比 b 大,然后把两个数相乘,,计算的过程用前缀和。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 100010;
int a[N],b[N],c[N],as[N],cs[N],s[N],cnt[N];
int main()
{
int n;
scanf("%d",&n);
for(int i = 0;i < n;i++) scanf("%d",&a[i]),a[i]++;
for(int i = 0;i < n;i++) scanf("%d",&b[i]), b[i]++;
for(int i = 0;i < n;i++) scanf("%d",&c[i]), c[i]++;
//计算as
for(int i = 0;i < n;i++) cnt[a[i]]++;
for(int i = 0;i < N;i++) s[i] = s[i - 1] + cnt[i];
for(int i = 0;i < n;i++) as[i] = s[b[i] - 1];
//把cnt s清空
memset(cnt,0,sizeof cnt);
memset(s,0,sizeof s);
//计算cs
for(int i = 0;i < n;i++) cnt[c[i]]++;
for(int i = 0;i < N;i++) s[i] = s[i - 1] + cnt[i];
for(int i = 0;i < n;i++) cs[i] = s[N - 1] - s[b[i]];
LL res = 0;
for(int i = 0;i < n;i++) res += (LL)as[i] * cs[i];
cout << res << endl;
return 0;
}
3.特别数的和
题目
小明对数位中含有 2、0、1、9 的数字很感兴趣(不包括前导 0),在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40,共 28 个,他们的和是 574。
请问,在 1 到 n 中,所有这样的数的和是多少?
输入格式
共一行,包含一个整数 n。
输出格式
共一行,包含一个整数,表示满足条件的数的和。
数据范围
1≤n≤10000
输入样例:
40
输出样例:
574
分析
代码
#include<iostream>
using namespace std;
int main()
{
int n,x;
cin >> n;
int res = 0;
for(int i = 1;i <= n;i++)
{
int t = i;
while(t)
{
x = t % 10;
t /= 10;
if(x == 2 || x == 0 || x == 1 || x == 9)
{
res += i;
break;
}
}
}
cout << res << endl;
return 0;
}
4. 错误票据
题目
某涉密单位下发了某种票据,并要在年终全部收回。
每张票据有唯一的ID号。
全年所有票据的ID号是连续的,但ID的开始数码是随机选定的。
因为工作人员疏忽,在录入ID号的时候发生了一处错误,造成了某个ID断号,另外一个ID重号。
你的任务是通过编程,找出断号的ID和重号的ID。
假设断号不可能发生在最大和最小号。
输入格式
第一行包含整数 N,表示后面共有 N 行数据。
接下来 N 行,每行包含空格分开的若干个(不大于100个)正整数(不大于100000),每个整数代表一个ID号。
输出格式
要求程序输出1行,含两个整数 m,n,用空格分隔。
其中,m表示断号ID,n表示重号ID。
数据范围
1≤N≤100
输入样例:
2
5 6 8 11 9
10 12 9
输出样例:
7 9
分析
关键在于字符串的分析,,两串字符,怎么弄一串。。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<sstream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main()
{
int cnt;
cin >> cnt;
string line;
getline(cin,line); //读取第一行的回车
while(cnt--)
{
getline(cin,line); //读取全部数据
stringstream ssin(line);
while(ssin >> a[n]) n++;
}
sort(a,a + n);
int res1 = 0,res2 = 0;
for(int i = 1;i < n;i++)
{
if(a[i] == a[i - 1]) res2 = a[i];
if(a[i] == a[i - 1] + 2) res1 = a[i] - 1;
}
cout << res1 << ' ' << res2 << endl;
return 0;
}
5.回文日期
题目
在日常生活中,通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用 8 位数字表示一个日期,其中,前 4 位代表年份,接下来 2 位代表月份,最后 2 位代表日期。
显然:一个日期只有一种表示方法,而两个不同的日期的表示方法不会相同。
牛牛认为,一个日期是回文的,当且仅当表示这个日期的8位数字是回文的。
现在,牛牛想知道:在他指定的两个日期之间(包含这两个日期本身),有多少个真实存在的日期是回文的。
一个 8 位数字是回文的,当且仅当对于所有的 i(1≤i≤8) 从左向右数的第i个数字和第 9−i 个数字(即从右向左数的第 i 个数字)是相同的。
例如:
•对于2016年11月19日,用 8 位数字 20161119 表示,它不是回文的。
•对于2010年1月2日,用 8 位数字 20100102 表示,它是回文的。
•对于2010年10月2日,用 8 位数字 20101002 表示,它不是回文的。
输入格式
输入包括两行,每行包括一个8位数字。
第一行表示牛牛指定的起始日期date1,第二行表示牛牛指定的终止日期date2。保证date1和date2都是真实存在的日期,且年份部分一定为4位数字,且首位数字不为0。
保证date1一定不晚于date2。
输出格式
输出共一行,包含一个整数,表示在date1和date2之间,有多少个日期是回文的。
输入样例:
20110101
20111231
输出样例:
1
分析
不能直接对所有的日期判断是不是回文数,,会超时的
反其道而行之:
先弄出这部分中所有的回文数,,然后判断是不是日期。。。。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
int months[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
bool check(int date)
{
int year = date / 10000;
int month = date % 10000 / 100;
int day = date % 100;
if(!month || month > 13 || !day) return false;
if(month != 2 && day > months[month]) return false;
if(month == 2)
{
bool leap = year % 4 == 0 && year % 100 || year % 400 ==0;
if(day > months[2] + leap) return false;
}
return true;
}
int main()
{
int date1,date2;
int res = 0;
cin >> date1 >> date2;
for(int i = 0;i < 10000;i++)
{
int r = i,x = i;
for(int j = 0;j < 4;j++) r = r * 10 + x % 10,x /= 10; //写出所有的回文
if(date1 <= r && r<= date2 && check(r)) res++;
}
cout << res << endl;
return 0;
}
6. 归并排序
题目
给定你一个长度为n的整数数列。
请你使用归并排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数 n。
第二行包含 n 个整数(所有整数均在1~109范围内),表示整个数列。
输出格式
输出共一行,包含 n 个整数,表示排好序的数列。
数据范围
1≤n≤100000
输入样例:
5
3 1 2 4 5
输出样例:
1 2 3 4 5
分析
双指针算法
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int N = 1000010;
int q[N],tmp[N];
void merge_sort(int q[],int l,int r)
{
if(l >= r) return;
int mid = l + r >> 1;
merge_sort(q,l,mid);
merge_sort(q,mid + 1,r);
int k = 0,i = l,j = mid + 1;
while(i <= mid && j <= r)
{
if(q[i] < q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
for(i = l,j = 0;i <= r;i++,j++) q[i] = tmp[j];
}
int main()
{
int n;
cin >> n;
for(int i = 0;i < n;i++) scanf("%d",&q[i]);
merge_sort(q,0,n - 1);
for(int i = 0;i < n;i++) printf("%d ",q[i]);
return 0;
}
7.移动距离
题目
X星球居民小区的楼房全是一样的,并且按矩阵样式排列。
其楼房的编号为 1,2,3…
当排满一行时,从下一行相邻的楼往反方向排号。
比如:当小区排号宽度为 6 时,开始情形如下:
1 2 3 4 5 6
12 11 10 9 8 7
13 14 15 …
我们的问题是:已知了两个楼号 m 和 n,需要求出它们之间的最短移动距离(不能斜线方向移动)。
输入格式
输入共一行,包含三个整数 w,m,n,w 为排号宽度,m,n 为待计算的楼号。
输出格式
输出一个整数,表示 m,n 两楼间最短移动距离。
数据范围
1≤w,m,n≤10000,
输入样例:
6 8 2
输出样例:
4
分析
蛇形矩阵
模拟
代码
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
int w,m,n;
cin >> w >> m >> n;
m--,n--;
int x1 = m / w,x2 = n / w;
int y1 = m % w,y2 = n % w;
if(x1 % 2 == 0) y1 = w - 1 - y1;
if(x2 % 2 == 0) y2 = w - 1 - y2;
cout << abs(x1 - x2) + abs(y1 - y2) << endl;
return 0;
}
8. 日期问题
题目
小明正在整理一批历史文献。这些历史文献中出现了很多日期。
小明知道这些日期都在1960年1月1日至2059年12月31日。
令小明头疼的是,这些日期采用的格式非常不统一,有采用年/月/日的,有采用月/日/年的,还有采用日/月/年的。
更加麻烦的是,年份也都省略了前两位,使得文献上的一个日期,存在很多可能的日期与其对应。
比如02/03/04,可能是2002年03月04日、2004年02月03日或2004年03月02日。
给出一个文献上的日期,你能帮助小明判断有哪些可能的日期对其对应吗?
输入格式
一个日期,格式是”AA/BB/CC”。
即每个’/’隔开的部分由两个 0-9 之间的数字(不一定相同)组成。
输出格式
输出若干个不相同的日期,每个日期一行,格式是”yyyy-MM-dd”。
多个日期按从早到晚排列。
数据范围
0≤A,B,C≤9
输入样例:
02/03/04
输出样例:
2002-03-04
2004-02-03
2004-03-02
分析
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int days[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
bool check(int year,int month,int day)
{
if(month == 0 || month > 12) return false;
if(day == 0) return false;
if(month != 2)
{
if(day > days[month]) return false;
}
else
{
int leap = year % 4 == 0 && year % 100 || year % 400 == 0;
if(day > 28 + leap) return false;
}
return true;
}
int main()
{
int a,b,c;
scanf("%d/%d/%d",&a,&b,&c);
for(int i = 19600101;i <= 20591231;i++)
{
int year = i / 10000,month = i / 100 % 100,day = i % 100;
if(check(year,month,day)) //判断是不是正常的年份
{
if(year % 100 == a && month == b && day == c || year % 100 ==c && month == a && day == b || year % 100 == c && month == b && day == a)
{
printf("%d-%02d-%02d\n",year,month,day);
}
}
}
return 0;
}
9.航班时间
题目
小 h 前往美国参加了蓝桥杯国际赛。
小 h 的女朋友发现小 h 上午十点出发,上午十二点到达美国,于是感叹到“现在飞机飞得真快,两小时就能到美国了”。
小 h 对超音速飞行感到十分恐惧。
仔细观察后发现飞机的起降时间都是当地时间。
由于北京和美国东部有 12 小时时差,故飞机总共需要 14 小时的飞行时间。
不久后小 h 的女朋友去中东交换。
小 h 并不知道中东与北京的时差。
但是小 h 得到了女朋友来回航班的起降时间。
小 h 想知道女朋友的航班飞行时间是多少。
对于一个可能跨时区的航班,给定来回程的起降时间。
假设飞机来回飞行时间相同,求飞机的飞行时间。
输入格式
一个输入包含多组数据。
输入第一行为一个正整数 T,表示输入数据组数。
每组数据包含两行,第一行为去程的起降时间,第二行为回程的起降时间。
起降时间的格式如下:
h1:m1:s1 h2:m2:s2
h1:m1:s1 h3:m3:s3 (+1)
h1:m1:s1 h4:m4:s4 (+2)
第一种格式表示该航班在当地时间h1时m1分s1秒起飞,在当地时间当日h2时m2分s2秒降落。
第二种格式表示该航班在当地时间h1时m1分s1秒起飞,在当地时间次日h2时m2分s2秒降落。
第三种格式表示该航班在当地时间h1时m1分s1秒起飞,在当地时间第三日h2时m2分s2秒降落。
输出格式
对于每一组数据输出一行一个时间hh:mm:ss,表示飞行时间为hh小时mm分ss秒。
注意,当时间为一位数时,要补齐前导零,如三小时四分五秒应写为03:04:05。
数据范围
保证输入时间合法(0≤h≤23,0≤m,s≤59),飞行时间不超过24小时。
输入样例:
3
17:48:19 21:57:24
11:05:18 15:14:23
17:21:07 00:31:46 (+1)
23:02:41 16:13:20 (+1)
10:19:19 20:41:24
22:19:04 16:41:09 (+1)
输出样例:
04:09:05
12:10:39
14:22:05
分析
处理字符串问题
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
int get_second(int h,int m,int s)
{
return h * 3600 + m * 60 + s;
}
int get_time() //读取一行时间
{
string line;
getline(cin,line); //getline(cin,str)函数是处理string类的函数。第二个参数为string类型的变量。读入时第二个参数为string类型
//转化为同样的格式
if(line.back() != ')') line += "(+0)";
int h1,m1,s1,h2,m2,s2,d;
sscanf(line.c_str(),"%d:%d:%d %d:%d:%d (+%d)",&h1,&m1,&s1,&h2,&m2,&s2,&d);
return get_second(h2,m2,s2) - get_second(h1,m1,s1) + d * 24 * 3600;
}
int main()
{
int n;
scanf("%d",&n);
string line;
getline(cin,line); //忽略第一行的回车
while(n--)
{
int time = (get_time() + get_time()) / 2;
int hour = time / 3600,minute = time % 3600 / 60,second = time % 60;
printf("%02d:%02d:%02d\n",hour,minute,second);
}
return 0;
}
10.外卖店优先级
题目
“饱了么”外卖系统中维护着 N 家外卖店,编号 1∼N。
每家外卖店都有一个优先级,初始时 (0 时刻) 优先级都为 0。
每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1,最低减到 0;而如果外卖店有订单,则优先级不减反加,每有一单优先级加 2。
如果某家外卖店某时刻优先级大于 5,则会被系统加入优先缓存中;如果优先级小于等于 3,则会被清除出优先缓存。
给定 T 时刻以内的 M 条订单信息,请你计算 T 时刻时有多少外卖店在优先缓存中。
输入格式
第一行包含 3 个整数 N,M,T。
以下 M 行每行包含两个整数 ts 和 id,表示 ts 时刻编号 id 的外卖店收到一个订单。
输出格式
输出一个整数代表答案。
数据范围
1≤N,M,T≤105,
1≤ts≤T,
1≤id≤N
输入样例:
2 6 6
1 1
5 2
3 1
6 2
2 1
6 2
输出样例:
1
样例解释
6 时刻时,1 号店优先级降到 3,被移除出优先缓存;2 号店优先级升到 6,加入优先缓存。
所以是有 1 家店 (2 号) 在优先缓存中。
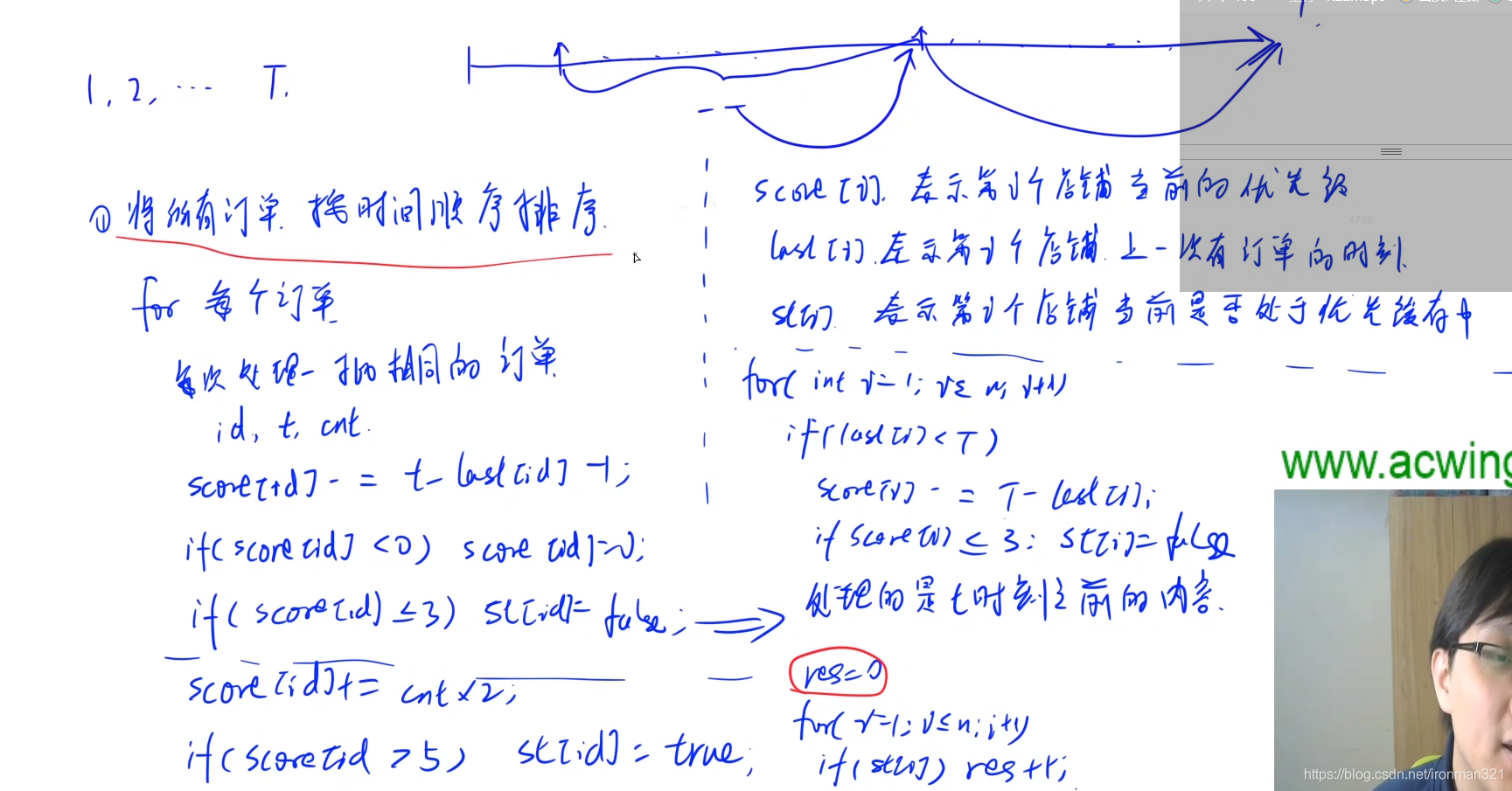
分析
把所有的连续的一段没有订单的时刻放到下个有订单的时刻去处理。。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N = 100010;
int n,m,T;
PII order[N];
int score[N],last[N];
bool st[N];
int main()
{
cin >> n >> m >> T;
for(int i = 0;i < m;i++)
scanf("%d%d",&order[i].x,&order[i].y);
//排序
sort(order,order + m);
for(int i = 0;i < m;)
{
//处理一批相同的订单
int j = i;
while(order[j] == order[i] && j < m) j++;
int t = order[i].x,id = order[i].y,cnt = j - i;
i = j;
//处理i之前的情况
score[id] -= t - last[id] - 1;
if(score[id] < 0) score[id] = 0;
if(score[id] <= 3) st[id] = false;
//处理i的情况
score[id] += cnt * 2;
if(score[id] > 5) st[id] = true;
last[id] = t; //表示id店铺上一个有订单的时间
}
//最后几个小时没有卖出去的情况
for(int i = 1;i <= n;i++)
{
if(last[i] < T)
{
score[i] -= T - last[i];
if(score[i] <= 3) st[i] = false;
if(score[i] < 0) score[i] = 0;
}
}
int res = 0;
for(int i = 1;i <= n;i++)
{
if(st[i]) res++;
}
cout << res << endl;
return 0;
}
11.逆序对的数量
题目
给定一个长度为n的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 i 个和第 j 个元素,如果满足 i < j 且 a[i] > a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1≤n≤100000
输入样例:
6
2 3 4 5 6 1
输出样例:
5
分析
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int cmp[N];
long long int res = 0;
void mergo_sort(int q[],int l,int r)
{
if(l >= r) return;
int mid = l + r >> 1;
mergo_sort(q,l,mid),mergo_sort(q,mid + 1,r);
//归并的过程
int i = l,j = mid + 1,k = 0;
while(i <= mid && j <= r)
{
if(q[i] <= q[j])
{
cmp[k++] = q[i++];
}
else
{
res += mid - i+ 1;
cmp[k++] = q[j++];
}
}
//扫尾的过程
while(i <= mid) cmp[k++] = q[i++];
while(j <= r) cmp[k++] = q[j++];
//临时数组还回去
for(int i = l,j = 0;i <= r;i++,j++) q[i] = cmp[j];
}
int main()
{
int n;
cin >> n;
int q[n];
for(int i = 0;i < n;i++) cin >> q[i];
mergo_sort(q,0,n - 1);
cout << res << endl;
return 0;
}





 本文精选了11道算法竞赛题目,涵盖了连号区间数、递增三元组、特别数的和等经典问题,提供了详细的解题思路与代码实现,适合算法初学者和竞赛选手学习参考。
本文精选了11道算法竞赛题目,涵盖了连号区间数、递增三元组、特别数的和等经典问题,提供了详细的解题思路与代码实现,适合算法初学者和竞赛选手学习参考。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








