[kuangbin]专题三 Dancing Links Treasure Map ZOJ - 3209【精确覆盖】

【题目描述】
Your boss once had got many copies of a treasure map. Unfortunately, all the copies are now broken to many rectangular pieces, and what make it worse, he has lost some of the pieces. Luckily, it is possible to figure out the position of each piece in the original map. Now the boss asks you, the talent programmer, to make a complete treasure map with these pieces. You need to make only one complete map and it is not necessary to use all the pieces. But remember, pieces are not allowed to overlap with each other (See sample 2).
你的老板曾经获得过很多份藏宝图副本。不幸的是，所有藏宝图副本现在都被破坏成了正方形碎片，并且更糟糕的是他丢失了一些碎片。幸运的是，可能可以找到原始地图的每个位置。现在老板要求你，天才程序员，使这些碎片变完整。你需要完善一张地图并且不需要使用所有碎片。但是记住，碎片不能互相重叠（详见样例2）。

【输入】
The first line of the input contains an integer T (T <= 500), indicating the number of cases.
第一行输入一个整数T(T <= 500)表示样例的数量。
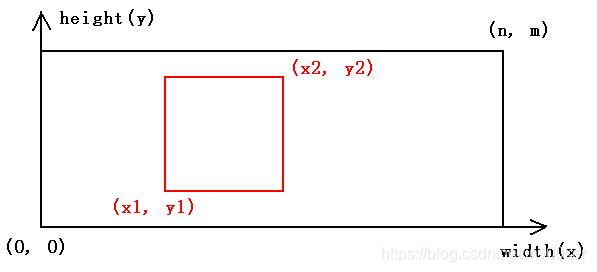
For each case, the first line contains three integers n m p (1 <= n, m <= 30, 1 <= p <= 500), the width and the height of the map, and the number of pieces. Then p lines follow, each consists of four integers x1 y1 x2 y2 (0 <= x1 < x2 <= n, 0 <= y1 < y2 <= m), where (x1, y1) is the coordinate of the lower-left corner of the rectangular piece, and (x2, y2) is the coordinate of the upper-right corner in the original map.
对于每个样例，第一行包含3个整数n,m,p (1 <= n, m <= 30, 1 <= p <= 500)，表示地图的宽度、深度和碎片的数量，后面p行每行包括4个整数x1,y1,x2,y2 (0 <= x1 < x2 <= n, 0 <= y1 < y2 <= m),(x1, y1)是左下角的坐标，(x2, y2)是右上角的坐标。
Cases are separated by one blank line.
样例用一个空行隔开。

【输出】
If you can make a complete map with these pieces, output the least number of pieces you need to achieve this. If it is impossible to make one complete map, just output -1.
如果你能用这些碎片使地图完整，输出使用碎片最小数目。如果不可能，输出-1。

【样例输入】
3
5 5 1
0 0 5 5

5 5 2
0 0 3 5
2 0 5 5

30 30 5
0 0 30 10
0 10 30 20
0 20 30 30
0 0 15 30
15 0 30 30

【样例输出】
1
-1
2

题目链接：https://cn.vjudge.net/problem/ZOJ-3209

DLX模板题，化三维为二维即可，M*N看作M，P看作N

代码如下：

#include <iostream>
using namespace std;
static const int MAXN=500+10;
static const int MAXM=900+10;
static const int MAXNODE=MAXN*MAXM+10;
struct DLX{
    int n,m,size;
    int U[MAXNODE],D[MAXNODE],R[MAXNODE],L[MAXNODE],Row[MAXNODE],Col[MAXNODE];
    int H[MAXN], S[MAXM];
    int ansd, ans[MAXN];
    void init(int _n,int _m)
    {
        n = _n;
        m = _m;
        for(int i = 0;i <= m;i++)
        {
            S[i] = 0;
            U[i] = D[i] = i;
            L[i] = i-1;
            R[i] = i+1;
        }
        R[m] = 0; L[0] = m;
        size = m;
        for(int i = 1;i <= n;i++)
            H[i] = -1;
    }
    void Link(int r,int c)
    {
        ++S[Col[++size]=c];
        Row[size] = r;
        D[size] = D[c];
        U[D[c]] = size;
        U[size] = c;
        D[c] = size;
        if(H[r] < 0)H[r] = L[size] = R[size] = size;
        else
        {
            R[size] = R[H[r]];
            L[R[H[r]]] = size;
            L[size] = H[r];
            R[H[r]] = size;
        }
    }
    void remove(int c)
    {
        L[R[c]] = L[c]; R[L[c]] = R[c];
        for(int i = D[c];i != c;i = D[i])
            for(int j = R[i];j != i;j = R[j])
            {
                U[D[j]] = U[j];
                D[U[j]] = D[j];
                --S[Col[j]];
            }
    }
    void resume(int c)
    {
        for(int i = U[c];i != c;i = U[i])
            for(int j = L[i];j != i;j = L[j])
                ++S[Col[U[D[j]]=D[U[j]]=j]];
        L[R[c]] = R[L[c]] = c;
    }
    void Dance(int d)
    {
        if(ansd!=-1 && d>=ansd)
            return;
        if(R[0] == 0)
        {
            if(ansd==-1)
                ansd=d;
            else if(ansd>d)
                ansd=d;
        }
        int c = R[0];
        for(int i = R[0];i != 0;i = R[i])
            if(S[i] < S[c])
                c = i;
        remove(c);
        for(int i = D[c];i != c;i = D[i])
        {
            ans[d] = Row[i];
            for(int j = R[i]; j != i;j = R[j]) remove(Col[j]);
            Dance(d+1);
            for(int j = L[i]; j != i;j = L[j]) resume(Col[j]);
        }
        resume(c);
    }
};
DLX dlx;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0),cout.tie(0);
    int T;
    cin>>T;
    while(T--)
    {
        int n,m,p;
        cin>>n>>m>>p;
        dlx.init(p,n*m);
        for(int i=1;i<=p;i++)
        {
            int x1,x2,y1,y2;
            cin>>x1>>y1>>x2>>y2;
            for(int x=x1+1;x<=x2;x++)
                for(int y=y1+1;y<=y2;y++)
                    dlx.Link(i,(x-1)*m+y);
        }
        dlx.ansd=-1;
        dlx.Dance(0);
        cout<<dlx.ansd<<endl;
    }
    return 0;
}