零知识证明之什么是QAP？什么是P/NP、NP完全问题(NPC问题)、NP hard问题？多项式时间

最新推荐文章于 2023-12-26 22:08:43 发布
原创 最新推荐文章于 2023-12-26 22:08:43 发布 · 2.3k 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#线性代数 #算法 #python

本文介绍了P与NP问题的概念，包括P问题在多项式时间内可解，NP问题在多项式时间内可验证但可能不可解。讨论了12字助记词的安全性，指出其安全性源于指数级的组合数量。接着，文章阐述了NP完全问题的定义和重要性，以旅行商问题为例。最后，详细解释了QAP（Quadratic Arithmetic Program）问题，它是NP完全问题的一种，用于算术电路的零知识证明。

文章目录

一、什么是NP问题

【强烈推荐】什么是P=NP问题？
参考URL: https://zhuanlan.zhihu.com/p/143003261
谈谈计算机中的NP，NP-Hard，NP完全以及"NP=P？"问题
参考URL: https://www.bilibili.com/video/BV1Wz4y1d7wb?from=search&seid=17069712980402004069
【计算机原理2】P=?NP和复杂度理论
参考URL: https://www.bilibili.com/video/BV1t54y1y7KN

在理解 QAP 之前，我们先来了解一下什么是 P 问题。
在这里插入图片描述

  • P问题是什么？
  • NP问题又是什么？
  • P=NP又是什么意思？
  • 研究并解决P=NP问题的意义是什么？

斯蒂芬·库克和列昂尼德·莱文在1971年独立地提出了P(即容易找到)和NP(即容易检查)问题。

P问题和NP问题的主要特征：

  • P 问题(easy to find)
    all problems solvable, deterministically, in polynomial time
    译：多项式时间内可解决的问题(当然在多项式时间是可验证的)

  • NP 问题(esay to check)
    non-deterministic Polynomial time
    译：非确定性多项式时间可解决的问题

举几个例子来加深印象：

计算1-1000的连续整数之和：这个问题就比较简单，无论是编程还是使用高斯求和公式都可以在有限可接受的时间内完成，这种算是P类问题。

计算地球上所有原子个数之和：这个问题就很困难甚至无解，但是现在有个答案是300个，显然是错的，所以很容易验证但不容易求解，这种算NP类问题。

P类问题是可以在多项式时间内解决并验证的一类问题，NP类问题是可以多项式时间验证但是不确定能否在多项式时间内解决的一类问题。

1. 多项式时间

【强烈推荐】什么是P=NP问题？
参考URL: https://zhuanlan.zhihu.com/p/143003261

多项式时间（英语：Polynomial time）在计算复杂度理论中，指的是一个问题的计算时间不大于问题大小的多项式倍数。任何抽象机器都拥有一复杂度类，此类包括可于此机器以多项式时间求解的问题。

其实多项式时间的概念我们还是很熟悉的，在做算法题或者日常工作时我们都会说，这个解法的时间复杂度是O(n^2)性能不是很好，那个解法的时间复杂度是O(nlogn)(注:计算机中的log一般指底数=2)还可以。

这里的大O就是时间复杂度的表示法，看到这里仿佛清晰一些了，不过还是看下多项式表达：
在这里插入图片描述
多项式的概念我们在小学初中的时候就开始接触了，对于计算机来说有更特别的含义，我们都知道算法时间复杂度的大O表示法，取表达式中的最高次其他项忽略，因为随着输入规模的增大最高次的影响最大，对计算机来说可以做这样的近似处理，比如上面的多项式表达式可以理解为O(n^k)的复杂度。

这个世界并不是只有多项式时间这么简单，我们还知道有指数函数形如 2 n 2^n 2n 这个计算量已经非常可怕，更不要说 n n n^n nn和 n ! n! n!这种问题了。

对于计算机而言，它不知道问题难不难，对它而言就是拆解成非常多的步骤去执行，去衡量计算机认为难或者不难或许可以从其执行时间来看，在排除代码实现差异来说，执行时间越长的问题通常都会比较难。

直观感受一下，随着不同输入规模下，多项式时间和非多项式时间的时间消耗曲线差异吧：
在这里插入图片描述看到这里恍然大悟，多项式时间内可解决的意义所在。

  • 多项式时间是算法复杂度的一个概念。
  • 问题元素为n时，若完成算法的指令条数为n的k次方（k为常数），那么这个算法是多项式时间算法。
  • 比如冒泡排序的时间复杂度是n的平方，就是一个多项式时间算法。
  • 如果指令条数为k的n次方或者n!之类的，就是非多项式时间算法。

回过头看看NP问题是non-deterministic Polynomial time，也就是NP问题能否在多项式时间内解决存在不确定性。

也就是说很多NP类问题如果无法在多项式时间内解决，那么于我们当前的计算能力而言是几乎无解的，量子计算机目前还处于初级阶段，或许若干年后这些问题对于量子计算机而言是可以接受的…

或许你会问像超级计算机这种能行吗？我们从时间增长曲线来看，问题规模扩大一点点，我们需要的算力就是更大倍数的增加，这样堆砌机器不是好办法，我们最好寄托于其他解决思路。

例如：
O(n) 是指规模增加多少，算法时间就增加多少。
像是从n个数里找出最小的数，把n个数过一遍就能找到。当n增大1个单位，算法时间也增加一个单位。

O(n^2)：算法时间增加的速度是规模增加的速度平方

复杂度包括：

  • 多项式复杂度：如O(1), O(n),O(n^a)
  • 非多项式复杂度：如O(a^n), O(n!), O(n^n)

那么，定义：有多项式复杂度的算法的问题为P类问题

2. 关于阶乘 n！

阶乘是基斯顿·卡曼（Christian Kramp，1760～1826）于 1808 年发明的运算符号，是数学术语。

一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!。 1808年，基斯顿·卡曼引进这个表示法。

亦即n!=1×2×3×…×(n-1)×n。阶乘亦可以递归方式定义：0!=1，n!=(n-1)!×n。

大于等于1
任何大于等于1 的自然数n 阶乘表示方法：
n ! = 1 × 2 × 3 × ⋯ × ( n − 1 ) × n n!=1\times 2\times 3\times\cdots \times (n-1)\times n n!=1×2×3×⋯×(n−1)×n
或
n ! = n × ( n − 1 ) ! n!=n\times (n-1) ! n!=n×(n−1)!

0的阶乘: 0 ！ = 1 0！= 1 0！=1

factorial
美: [fæk’tɔriəl]
英: [fæk’tɔːriəl]
adj. 【数】因数的；阶乘的；代理商的；工厂的
n. 阶乘
网络 因子的；阶乘函数；阶乘因数的

Latex 语法：
乘号 分号
\frac{}{}:分号
\times: 乘号
省略号命令：水平方向\cdots 竖直方向\vdots 对角线方向\ddots

12字助记词真的安全吗？

12字助记词真的安全吗？真相在这里
参考URL: https://www.sohu.com/a/250920831_100244496

比特币地址如此安全的原因在于它们隐藏在如浩瀚宇宙天文数字般庞大的的数字海洋中，无论你花费了多少时间和精力去破解地址，你随机猜测别人的私钥的机会基本上接近零。

一个典型的比特币地址长这样：1G1W1DbeUeH2AKKicqMNuhEuaoqPDNuXDF. 它由34个字符组成，包含大小写字母、数字，代表的是一个庞大的数字，将它翻译成数字是这样子的：4,036,794,190,046,444,310,490,975,774,115,813,708,619,807,673,368,708,224,110. 普通人是很难想象如此庞大的数字。要知道这串数字的庞大程度，我们可以通过一些想象练习来了解这串数字。全世界可能存在的比特币地址总数量可以表示为2^160个。

想象一个象棋棋盘，每一个格子代表一把密钥及其对应的比特币地址，如果这个棋盘包含了全世界可能存在的比特币地址总数，也就是2^160个，那么这个棋盘的每条边长将为2^80英寸。

2^80英寸是多长？如果大家熟悉光年（长度单位，用来计量光在宇宙真空中沿直线传播一年时间的距离，Light years）这个概念的话，那就相当于3,245,772光年那么长。这就意味着，如果你在一艘宇宙飞船上以光年速度破解比特币地址，也要花上300多万年才能破解一列的地址。

在宇宙飞船上一秒，你可能已经检验了棋盘上11,802,852,677个格子。118亿个地址听起来好像非常之多，但这只是300多万年中的一秒。可想这里数字之庞大浩瀚！

另外，要快速破解尽可能多的地址，需要投入什么资源呢？所有计算能力的都来自比特币网络本身，它使用了地球上最强大和高度专业化的计算机。比特币网络的速度比全球排名前500的超级计算机速度总和还要快10万倍。假设我们已经说服所有这些硬件拥有者愿意将设备借给我们进行实验。 今天的比特币网络每秒可以在棋盘上搜索大约4,000,000万亿个格子。这肯定比我们的宇宙小飞船要快得多！在这个速度下，我们需要多长时间才能检查棋盘上的一个完整列？答案是大约3.5天至超过300万年之间！不过大家还要明白一点，要检验完一个完整列，在电费的开销方面将高达$750万美金。再者，从这些地址里能收获多少比特币？答案是零。

BIP39钱包助记词规范
参考URL: https://www.jianshu.com/p/d5bac6d36dc6
比特币助记词，是固定词库，总共2048个单词，https://github.com/bitcoin/bips/blob/master/bip-0039/english.txt

现在应用最广的BIP39助记词标准，助记词字典里有2048个单词。
现行助记词标准一般有12词和24词两种12词组合的可能性是2048^12 = 5.44e39, 24 词组合可能性是 2048^24 = 2.96e79

10^79 这个数量级接近宇宙里所有原子的数目，所以暴力破解是不可能的。

BIP39 规定了助记词和种子生成规则。这些单词取自一个固定词库，词汇生成有一定规矩和顺序，词库共有 2048 个单词。
不是随便输入 24 个单词就能生成加密货币地址的，也不能随意选择自己喜欢的词，或者随意组合词汇。
而两个人选到一模一样（词汇一样+顺序一样）的 24 个词的概率有多大呢？可以说这几乎是不可能事件，2048 的 24 次方之一，仿若在宇宙中找一颗原子那么困难。

3. 现实中的NP类问题

其实现实中的 NP 类问题非常多，并且很多都有非常重要的意义，举几个大家耳熟能详的例子，比如旅行商问题(又称旅行推销员问题)。

大整数分解
比如：求大整数99400891的2个质因子是困难的，但是若告知9967、9973,验证它们是99400891的2个质因子是可以在多项式时间内实现的。

知乎问题：为什么说宇宙原子总数差不多是10的80次方？
https://www.zhihu.com/question/63852727

这个数字是按照宇宙中星系数量、每个星系恒星数量、每个恒星质量等角度结合原子质量进行的估算，数量级上有一些误差，但是远小于100的阶乘，这里我们深深感受了指数级膨胀的威力。

所以当TSP问题的输入规模在100时，如果仍然进行穷举的话，计算量将无效大，天荒地老沧海桑田那种…

NP问题不仅存在于运筹学，在医学领域的蛋白质折叠问题也属于NP问题，该问题对研究癌症、阿尔兹海默症、帕金森症等都有非常重大的现实意义。

所以对于NP类问题的现实影响意义我们不用质疑，充分认识到这类问题的研究价值所在是我们进步的源动力。

二、P是否等于NP, N=NP是否成立

【妈咪说-推荐】P=NP是啥？玩数独就可以得100万，你信吗？看完就懂了！
https://www.bilibili.com/video/av26274880/

这是一个与黎曼猜想齐名的问题，位列七大千禧年难题之一。如果你能破解它，不仅能够功成名就，满目繁花，更能收获100万美元奖金。这就是理论计算机科学的圣杯：P/NP问题。

有些科学家认为，所有的NP问题终究都可以在多项式时间内解决，只是我们暂时还没有找到方法；也有些科学家认为，某些NP问题永远无法在多项式时间内解决。

P问题是肯定是NP问题（你再多项式时间内可解，自然肯定在再多项式时间内科验证），但是NP是不是P问题，这个就是那个传说中的世界难题。

破解密码就是一个NP 问题，因为你输入一个密码计算机能够瞬间验证密码是否正确。然而它却不一定是个P问题，目前的算法还无法在多项式时间内解决最先进的加密算法。

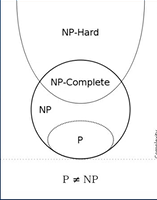
三、什么是NP完全或NP完备

参考URL: https://www.bilibili.com/video/BV1Wz4y1d7wb?from=search&seid=4031955861848542673
https://www.bilibili.com/video/BV187411n7zC?from=search&seid=9440287660052340793

npc，指NP完全问题（Non-deterministic Polynomial complete problem），是经过证明的不能用多项式时间复杂度解决的问题。

NPC问题能够通过多项式时间复杂度的算法进行检验而无法通过多项式时间复杂度的算法转化为P问题，故NPC问题常常为最为困难的一类问题。

在这里插入图片描述

  1. 证明N P = P   思路之一 ：问题约化
    可以用问题B的算法来解决A ，我们就说问题A可以约化成问题B。

例如：
问题A :
3 x + 6 = 12 3x + 6 = 12 3x+6=12 (采用一元一次方程的解法)
问题B :
0 ∗ x 2 + 3 x + 6 = 12 0*x^2 + 3 x + 6 = 12 0∗x2+3x+6=12

显然问题A可以约化为问题B，如果证明了一元二次方程的解法是多项式时间算法，则说明一元一次方程的解法也是多项式时间算法。

约化具有传递性: A约化为B，B约化为C

把众多的NP问题层层约化，必定会得到一个或多个“终极问题”，这些约化的终点就是所谓的NPC问题（NP-complete）

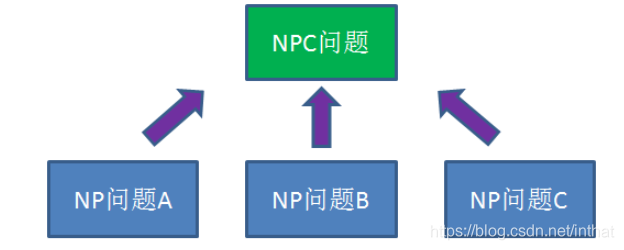
在这里插入图片描述
2. NPC问题的2个条件

  • 自身是NP问题；
  • 其他NP问题能约化到它；

如果所有NP问题可在多项式时间内约化成某个NP问题，则该NP问题称为NP完全问题。

四、什么是QAP？

IPFS星想法｜零知识证明 – 从QSP到QAP
参考URL: https://www.lbaike.cn/100440/

  • SP - Span Program ，采用多项式形式实现计算的验证。

  • QSP - Quadratic Span Program，QSP问题，实现基于布尔电路的NP问题的证明和验证。

    QAP 是 Quadratic Arithmetic Program 的缩写。
    QAP - Quadratic Arithmetic Program，QAP问题，实现基于算术电路的 NP问题的证明和验证，相对于QSP，QAP有更好的普适性。

  • QSP/QAP 问题的思想都是出自 2012 年一篇论文：Quadratic Span Programs and Succinct NIZKs without PCPs。论文的下载地址： https://eprint.iacr.org/2012/215.pdf

  • SNARG – Succinct Non-interactive ARGuments，简洁的无须交互的证明过程。

  • SNARK – Succinct Non-interactive ARgumentss of Knowledge，相比SNARG，SNARK多了Knowledge，也就是说，SNARK不光能证明计算过程，还能确认证明者“拥有”计算需要的Knowledge（只要证明者能给出证明就证明证明者拥有相应的解）。

  • zkSNARK – zero-knowledge SNARK，在SNARK的基础上，证明和验证双方除了能验证计算外，验证者对其他信息一无所知。

  • Statement – 对于QSP/QAP而言，某个计算电路的输入。Statement对证明者和验证者都是公开的。

  • Witness – Witness只有证明者知道。可以理解成，某个计算电路的输出（output）。

QAP问题和算术电路

QAP的定义和QSP的定义有些相似（毕竟都是一个思想理论的两种形式）。论文中给出了QAP的一般定义和强定义。QAP的强定义如下：

在这里插入图片描述算术电路可以简单看成由如下的三种门组成：加门，系数乘法门以及通用乘法门（减法可以转化为加法，除法可以转化为乘法）。Vitalik在2016年写过的QAP介绍，深入浅出的解释NP问题的算术电路生成和QAP问题的转化。推荐大家都读一读。

https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

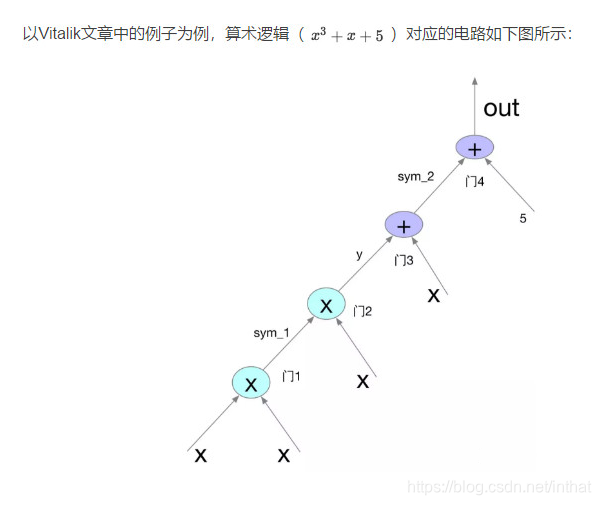
在这里插入图片描述

PS，未复制完全，需要可以查看原文。什么是QAP？ 其实就是一个具体的NPC问题。因为NPC有个特性，所有NP问题（包括NPC）能归约（转换）到它。所以一些零知识证明实现也就是基于QAP。

总结：QAP和QSP问题类似。QSP问题主要用于布尔电路计算表达，QAP问题主要用于算术电路计算表达。将一个算术电路计算转化为QAP问题的过程，其实就是对电路中每个门电路进行描述限制的过程。通过朗格朗日定理，实现算术电路的多项式表达。QAP问题的zkSNARK的证明验证过程和QSP非常相似。

五、参考

硬核科普来了~二十分钟理解 P 和 NP 问题
参考URL: https://www.bilibili.com/video/BV1eE41167c4?from=search&seid=17069712980402004069
数独和蛋白质折叠本质是同一问题？P vs. NP问题科普
参考URL: http://code.dev.xdja.com/D26420
谈谈计算机中的NP，NP-Hard，NP完全以及"NP=P？"问题
参考URL: https://www.bilibili.com/video/BV1Wz4y1d7wb?from=search&seid=17069712980402004069
活动作品NP问题、密码算法 P/NP/NP难度/NPC 信息安全的目标 对称、非对称密码体制 RSA算法
参考URL: https://www.bilibili.com/video/BV1iD4y1m7Qi
【计算机原理2】P=?NP和复杂度理论
参考URL: https://www.bilibili.com/video/BV1t54y1y7KN
【妈咪说-推荐】P=NP是啥？玩数独就可以得100万，你信吗？看完就懂了！
https://www.bilibili.com/video/av26274880/
用晶体管构造门电路
参考URL: https://www.maixj.net/ict/jingtiguan-mendianlu-23007
布尔运算，二进制和门电路
参考URL: https://hzcyacom.blog.youkuaiyun.com/article/details/109219345

零知识证明(Zero-Knowledge Proof)入门指南
qq_42568323的博客
07-12 732
零知识证明（Zero-Knowledge Proof, ZKP）是一种密码学协议，允许证明者在不泄露任何实际信息的情况下向验证者证实某个陈述的真实性。它具有完备性、可靠性和零知识性三大核心特性，可通过洞穴寓言等通俗示例理解其原理。ZKP主要分为交互式（如Schnorr协议）和非交互式（如zk-SNARKs）两类，后者更适合区块链应用。其数学基础包括同态加密、椭圆曲线密码学和离散对数问题。文章还提供了Schnorr协议的Python实现示例，并简要介绍了zk-SNARKs的工作流程及其R1CS和QAP转换方法
Quadratic Assignment Problem 二次分配问题 QAP
AS7062031的博客
08-31 1万+
二次分配问题（QAP）是数学优化或运筹学分支中最基本的组合优化问题之一，从Koopmans和Beckmann [1]首次提出的设施选址问题的范畴来看。 该问题模拟了以下现实生活中的问题： QAP问题可描述为：已知有n个位置和n家工厂，各位置之间的距离矩阵设为D=(dij)n*n，各工厂之间的运输量矩阵为F=(fij)n*n。现要将这n家工厂建造在这n个位置上，使得总费用最小。 设dij表示位置i与位置j之间的距离，fij位置i与位置j之间的费用。故工厂i建造在位置k且工厂j建造在位置l所导致的费...
零知识 QAP 问题的转化
xiaozhupeiqi321的博客
05-31 1375
简介：本文是 Vitalik 写于 2016 年 12 月，用于介绍零知识证明的数学实现方式的论文。文章思路清晰，通俗易懂，也因此，该文成为区块链行业技术人员学习这方面知识的首选文章之一。 术语介绍 解决一个问题需要花费时间。如果解决问题需要的时间与问题的规模之间是多项式关系，则可以称该问题具有多项式复杂度。 P 问题*：指的是在多项式时间内可解的问题。* NP 问题*（Non-Deterministic Polynomial Problem，非确定性多项式问题）：指不能在多项式内可解，但是可以在多
Quadratic Assignment Problem 二次分配问题
qq_39591612的博客
12-26 2194
主要使用c++算法对问题进行求解，包括随机算法，贪心算法，蚁群算法以及模拟退火算法法
zkSnarks：QAP上构造零知识证明
qq_34793644的博客
03-23 1202
协议一：抽样验证：prover向验证证明它知道一个d阶多项式 verifier：选取随机数s，发送给prover prover：计算h(x) = P(x)/t(x) ，公开p(s) 、h(s)。 verifier：验证等式p(s) = t(s) h(s)是否成立 该证明了prover知道一个整除t(x)的多项式，但存在以下问题： prover 知道s，可以计算出t(s), 随机选取h(s) ,并构造p(s) = t(s) h(s) prover 知道点(s, t® h®), 可以构造
02. Zero-KNOWLEDGE for All NP【对于所有NP问题的零知识】
qq_43479839的博客
01-26 1199
02. Zero-KNOWLEDGE for NP【对于NP的零知识证明】 这篇博客，是关于第九届BIU密码学冬令营上的内容，这篇博客是第二篇，会持续更新。 01.Introduction to Zero knowledge --Alon Rosen [零知识证明介绍]的链接如下： https://blog.youkuaiyun.com/qq_43479839/article/details/112985426 也可以在我之前的这篇博客中，去寻找一些关于其它知识点的博客，下面的博客链接是我整个内容的目录博客，如果有
PSO - QAP_利用PSO解决QAP问题_pso问题_
10-04
该程序利用PSO算法解决QAP问题，程序已经调试好，可以直接上手。
基于标准PSO、自适应PSO、量子PSO、PSO-GA、PSO-GSA算法求解三个NP问题：TSP、QAP、背包问题研究附Matlab代码.rar
04-27
在当前的计算机科学和运筹学领域，粒子群优化（Particle Swarm Optimization, PSO）算法是一种有效的全局优化算法，它模拟鸟群的觅食行为来求解优化问题。标准PSO是这一算法的最初形式，而自适应PSO、量子PSO、PSO...
QAPLib.rar_QAPLIB_QAP问题_qap_二次分配_二次分配问题
07-14
优化问题中方的经典问题二次分配问题QAP测试数据
P、NP、NP-hard、NPC问题超简单理解
THMAIL的博客
09-30 3518
查了好多资料，现在网上的资料都不说人话，简单的问题故意写得让别人看懂不以显示自己的水平很高深？真正的大师难道不是把复杂问题说得很简单的人？把简单问题说得让别人看不懂显得自己很高深的就是煞笔。 多项式定义：就是一元N次方式，时间复杂度为多项式的问题都很容易解出来 各类问题关系图： （结合以下文字说明看） 问题定义： P问题：一个问题可以在多项式（O(n^k)）的时间复杂度内解决（简单的问题）； 例如：n个数的排序问题（不超过O(n^2)） NP问题：一个问题的解可以在多项式的时间内被证实或证伪，即给
funcode——坦克大战
05-17
基于funcode的坦克大战设计，添加多种元素，界面更加美观，添加各种音效。
概念辨析 P、NP、NPC、NP-hard
qq_42258321的博客
06-13 1469
写在前面 最近在看老师的论文，看到论文中的NP-hard，co-NP-hard问题，虽然自己知道这是什么问题，但还是觉得有必要对P、NP、NPC、NP-hard、co-NP-hard问题的概念进行辨析，毕竟弄清楚问题的概念是解决问题的第一步 小故事引言 先来看一个小故事，假如老板要你解决一个问题，你绞尽脑汁还是想不出来，叫天天不应，叫地地不灵，这时你走进老板办公室，可以采取3种策略： ...
python:# noqa
Crazy_zh的博客
12-09 3871
看flask源码时发现好多import后面都有# noqa注释，去查了下，是使用flake8进行代码检查时，不检查那一行的意思。 在vscode中试了一下，使用pylint进行代码检查时报错： 换成flake8： 不提示错误了，去掉注释： ...
我的隐私计算学习——零知识证明
weixin_47695607的博客
11-27 2649
安全保护技术（五）
零知识证明 SNARKs 第5部分：从计算到多项式
跨链技术践行者
03-28 1万+
In the three previous parts, we developed a certain machinery for dealing with polynomials. In this part, we show how to translate statements we would like to prove and verify to the language of poly...
通俗易懂：P问题、NP问题、NPC问题和NP-hard问题
南七行者的博客
11-10 4271
一、基础知识 1.现实中的问题(比如：排序问题)，存在很多解决办法(即计算机领域的算法)，所以需要衡量算法的性能。 一个算法的优劣主要从算法的执行时间(即时间复杂度)和所需要占用的存储空间(即空间复杂度)两个方面衡量。 P类问题和时间复杂度有关，所以本文只谈时间复杂度。 2.时间复杂度 若对排序算法有了解的小伙伴，大多是知道冒泡排序的平均时间复杂度为O(n2n^2n2)，按照多项式的定义(形如an⋅xn+an−1⋅xn−1+...+a1⋅x+a0a_n·x^n + a_{n-1}·x^{n-1} + .
零知识证明（zero-knowledge proof）
Carl_Zhang
01-07 2万+
零知识证明（zero-knowledge proof） 在密码学中，零知识证明(zero-knowledge proof)或零知识协议(zero-knowledge protocol)是一种方法，通过该方法，一方（the prover, 证明者）可以向另一方（the verifier, 证明者）证明他们知道值x，而无需传达任何信息，除了他们知道值x。零知识证明的本质是，通过简单地揭示信息来证明某人...
QAP，社会网络分析假设检验之一
热门推荐
HouGISer的博客
11-09 4万+
一 简介 参考刘军的《整体网分析讲义》和《社会网络分析导论》，对QAP进行一些总结。 在社会网络分析中，有一种方法用来研究关系之间的关系，通俗来讲，就是研究两个方阵的相关性和回归性。这种方法叫做QAP(Quadratic Assignment Procedure，二次指派程序)。它对两个方阵各个格值的相似性进行比较，给出两个矩阵之间的相关系数，同时对系数进行非参数检
QAP问题 change in cost是什么
最新发布
10-07
QAP（Quadratic Assignment Problem）即二次分配问题，是一个经典的组合优化问题。在QAP中，成本变化（change in cost）指的是在对问题的解进行某种调整（如交换两个设施的分配位置等）后，目标函数值的改变量。 在QAP里，目标是将一组设施分配到一组位置上，使得总成本最小。总成本通常由设施之间的流量和位置之间的距离共同决定，目标函数是一个二次函数。当对当前的分配方案进行改变时，比如把原本分配到位置A的设施i和分配到位置B的设施j进行交换，就会产生新的分配方案，此时新方案的总成本与原方案总成本的差值就是成本变化。 例如，原方案的总成本是 $C_1$，经过某种操作（如设施交换）后新方案的总成本是 $C_2$，那么成本变化 $\Delta C = C_2 - C_1$。如果 $\Delta C < 0$，说明新方案的成本更低，这种改变是有益的，可以考虑接受新方案；如果 $\Delta C > 0$，则新方案成本更高，通常在追求最小成本的情况下不会轻易接受该新方案，但在一些启发式算法（如模拟退火算法）中，即使 $\Delta C > 0$ 也可能以一定概率接受新方案，以避免陷入局部最优解。 成本变化在求解QAP的许多算法中都起到关键作用。例如在局部搜索算法中，通过不断计算成本变化来寻找更优的邻域解，不断迭代直到无法找到更优的邻域解为止；在禁忌搜索算法中，成本变化也是判断是否移动到新解的重要依据之一。 ```python # 以下是一个简单示例，模拟在QAP中交换两个设施分配位置后计算成本变化 import numpy as np # 定义设施之间的流量矩阵 flow = np.array([[0, 2, 3], [2, 0, 1], [3, 1, 0]]) # 定义位置之间的距离矩阵 distance = np.array([[0, 5, 6], [5, 0, 4], [6, 4, 0]]) # 定义初始分配方案 assignment = np.array([0, 1, 2]) def calculate_cost(flow, distance, assignment): cost = 0 n = len(assignment) for i in range(n): for j in range(n): cost += flow[i][j] * distance[assignment[i]][assignment[j]] return cost # 计算初始成本 initial_cost = calculate_cost(flow, distance, assignment) # 交换设施0和设施1的分配位置 new_assignment = assignment.copy() new_assignment[0], new_assignment[1] = new_assignment[1], new_assignment[0] # 计算新成本 new_cost = calculate_cost(flow, distance, new_assignment) # 计算成本变化 change_in_cost = new_cost - initial_cost print(f"初始成本: {initial_cost}") print(f"新成本: {new_cost}") print(f"成本变化: {change_in_cost}") ```
评论 2
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

西京刀客

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值