一. 总览
链表是算法设计题的重点考查章节,由于链表的算法题的代码量相对较少,又具有一定的算法设计技巧,因此适合笔试考查。
二. 链表初始化
以下内容为 双向链表的初始化,后续的题目中的代码实现都是基于此处的。若后续题目要求为 循环单链表、循环双向链表等等,读者自行增删以下的初始化代码即可
#include <iostream>
using namespace std;
typedef struct node
{
int data;
struct node* next;
struct node* pre;
}Node, *LinkList;
LinkList initList()
{
LinkList l = (Node*)malloc(sizeof(Node));
if (l == NULL)
{
printf("分配内存失败");
return NULL;
}
else
{
l->next = NULL;
}
return l;
}
三. 题型拆分剖析
1. 删除结点-----------基础操作

void del(LinkList l, int a, int b)
{
Node* pr = l;
Node* p = l->next;
while (p != NULL)
{
if (p->data > a && p->data < b)
{
Node* temp = p;
p = p->next;
pr->next = p;
free(temp); // 释放内存
temp = NULL;
}
else {
pr = p;
p = p->next;
}
}
}
指针temp : 只是一个变量,存储的是一个内存地址,占用的是 栈内存
temp 指向的内存 : 是malloc申请的 堆内存,这部分内存需要手动释放
(比如 malloc(sizeof(Node)) 或 new Node )free(temp)的作用 : 释放 temp 指向的 堆内存,而不是释放指针变量本身
2. 两个链表交集--- 归并思想

归并思想:通过双指针同步遍历多个有效序列,在遍历过程中比较元素大小and合并结果,从而将时间复杂度优化到 O(m+n)(m和n分别为两个序列的长度)
算法设计:
1. 采用归并思想,设置两个工作指针,对两个链表进行归并扫描,保留交集,其余结点释放
2. 当一个链表遍历完毕后,释放另一个表中的其余结点。
void Get_Intersection(LinkList A, LinkList B)
{
Node* pa = A->next;
Node* pb = B->next;
Node* temp = NULL;
Node* pc = A; // 用于构建结果链表
while (pa != NULL && pb != NULL)
{
if (pa->data == pb->data)
{
pc->next = pa; // 删除 非交集结点
pc = pa; // 移动pc 指向交集结点
pa = pa->next;
temp = pb; // 暂存pb 用来释放b中的交集结点
pb = pb->next;
free(temp);
}
else if (pa->data < pb->data)
{
temp = pa;
pa = pa->next;
free(temp);
}
else
{
temp = pb;
pb = pb->next;
free(temp);
}
}
// 循环结束,必然满足pa == NULL或 pb == NULL(即至少一个链表已遍历完)
while (pa != NULL)
{ // 假设B先遍历完,此时A中还有剩余节点,释放A中剩余的结点
temp = pa;
pa = pa->next;
free(temp);
}
while (pb != NULL)
{ // 假设A先遍历完,此时B中还有剩余节点,释放B中剩余的结点
temp = pb;
pb = pb->next;
free(temp);
}
pc->next = NULL; // 主循环while执行后,pc移动到了末尾
free(B); // 释放B的头节点
}
3. 连续子序列-------字符匹配

bool isContinuousSunsequence(LinkList A, LinkList B)
{
Node* pa = A->next;
Node* pb = B->next;
Node* start = NULL;
while (pa != NULL)
{
if (pa->data == pb->data)
{
if (start == NULL)
{
start = pa; // 记录起始匹配位置
}
pb = pb->next;
if (pb == NULL) // B 已遍历完毕
{
return true;
}
}
else
{
pb = B->next; // 重置 pb 位置
if (start != NULL)
{
//代码执行前,start指向 匹配成功的结点
pa = start->next;
start = NULL;
continue; // 跳转到 while(pa != NULL),不会移动pa
}
}
pa = pa->next;
}
return false;
}
4. 访问频度域-------多循环条件嵌套

注:将题目中的 pred 改为 pre
Node* Locate(LinkList L, int x)
{
Node* p = L->next;
Node* target = NULL;
// 查找数据为 x 的结点
while (p != NULL)
{
if (p->data == x)
{
target = p;
target->freq++;
break;
}
p = p->next;
}
// 未找到目标结点,返回NULL
if (target == NULL)
{
return NULL;
}
// 向前调整节点位置,保持 freq 递减 && 最近访问在前(频度相同)
// 从当前节点的前驱 开始比较
// 循环条件解析:前指针不等于头指针 && 保持 freq 递减 || 若频度相同,最近访问在前
p = target->pre;
while (p != L && (target->freq > p->freq || (p->freq == target->freq && p->next != target)))
{
target->pre = p->pre;
p->pre->next = target;
p->pre = target;
p->next = target->next;
if (target->next->pre != NULL)
{
target->next->pre = p;
}
target->next = p;
// 继续向前
p = target->pre;
}
// 返回找到的结点地址
return target;
}
5. 多次头插法-------成环与断环

成环与断环:将单链表首尾相连,以便确认尾节点
void move_node(LinkList l,int k)
{
// 计算n的个数
int n = 1; // while 循环内代码执行顺序特殊,n从1开始
Node* p = l->next;
while (p->next != NULL)
{
p = p->next;
n++;
}
// 成环
p->next = l;
// 寻找新首元节点
for (int i = 1; i <= n - k; i++)
{
p = p->next;
}
// 断环
l = p->next; // l 指向新首元结点
p->next = NULL; // 断环
}
6. 链表有无环-------快慢双指针

环检测算法(Floyd判圈法):需要 慢指针每次走一步,快指针每次走两步
数学推导:
设 头节点到环入口的距离为 a ,环入口到 快慢指针 第一次相遇点的距离为 b,相遇点到环入口的距离为 c
因此 环的总长度为 b+c
当两者第一次相遇时:慢指针走过的距离为: a+b ;快指针:2*(a+b)
深入考虑:快指针在达到相遇点前,已经绕环至少一圈,因此 总距离可以表示为
a+b+k*(b+c) (k是快指针绕环的圈数)(k >= 1)
2*(a+b) = a+b+k*(b+c)
a+b = k*(b+c)
a = k*(b+c) - b
a = (k-1)*(b+c) + c :快指针从相遇点出发,走c步,必然到达换环入口
a = (k-1)*(b+c) + c
即 慢指针从起点 走a步 = 快指针从相遇点出发,走c步(此时,即第一次相遇后,快慢指针每次都走一步)
整体分析:
第一次相遇前:快指针每次走两步,慢指针每次走一步
第一次相遇后:慢指针被重置到头节点,快指针保留在相遇点,此后均以每次1步的速度移动,直至第二次相遇,此时的相遇点,即为环入口
Node* detect_Cycle(LinkList l)
{
Node* slow = l->next;
Node* fast = slow->next;
while (fast != NULL && fast->next != NULL)
{
if (slow == fast)
{
slow = l->next; // 重置慢指针
while (slow != fast)
{
slow = slow->next;
fast = fast->next; // 相遇后,每次走一步
}
return slow;
}
slow = slow->next;
fast = fast->next->next;
}
return NULL;
}
7. 比较最大和-------反转指针指向
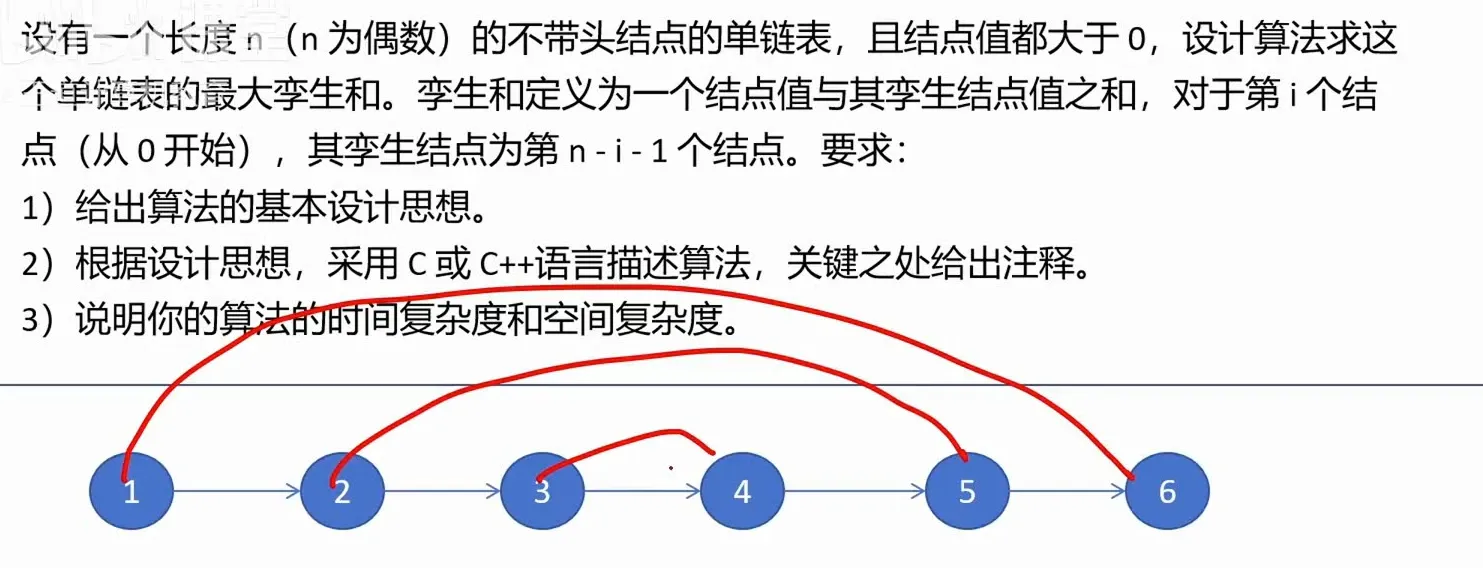
算法设计思想:
- 利用双指针法,先通过遍历链表找到中间位置,将链表后半部分反转
- 同时遍历 原链表前半部分 和 反转后的后半部分,计算和,比较最大和
- 最后可选择恢复链表结构(若有需求)
int maxTwinSum(LinkList l, int n)
{
// 1.找中间节点
Node* slow = l->next;
Node* fast = l->next;
while (fast != NULL && fast->next != NULL)
{
slow = slow->next;
fast = fast->next->next;
}
// 此时 slow 指向 后半部分第一个结点,fast指向NULL
// 2.反转后半链表(反转的是指针,并非旋转后半链表)
Node* prev = NULL;
Node* curr = slow;
Node* nextNode = NULL;
while (curr != NULL)
{
nextNode = curr->next; // 保存下一个结点
curr->next = prev; // 反转当前结点指针
prev = curr; // 移动 prev 到当前结点
curr = nextNode; // curr 指向下一个结点
}
// 此时curr指向为NULL,prev指向最后一个结点
// 3.计算比较最大和
Node* p1 = l->next; // 前半部分指针
Node* p2 = prev; // 后半部分指针
int maxSum = 0;
int currentSum = 0;
while (p2 != NULL)
{
currentSum = p1->data + p2->data;
if (currentSum > maxSum)
{
maxSum = currentSum;
}
p1 = p1->next;
p2 = p2->next;
}
return maxSum;
}
8. 删除结点-----------空间换时间

题目分析:
- 时间复杂度尽可能高效:建立辅助数组
- |data| <= n : data的取值范围为 [0,n] ,共 n+1 种可能 ,因此数组的大小可设置为 n+1
- 数组的下标 对应 |data| ,数组下标对应的值 为 0 表示未出现,1 表示已出现。此操作实现 以 O(1)时间 判断节点是否需要删除,避免重复遍历
typedef struct node
{
int data;
struct node* link;
}Node, *LinkList;
void del_node(LinkList head, int n)
{
int* p = (int*)malloc(sizeof(int) * (n + 1));
for (int i = 0; i < n + 1; i++)
{
p[i] = 0;
}
Node* prev = head;
Node* curr = head->link;
while (curr != NULL)
{
if (p[abs(curr->data)] == 1)
{
prev->link = curr->link;
free(curr);
curr = prev->link;
}
else
{
p[abs(curr->data)] = 1;
prev = curr;
curr = curr->link;
}
}
free(p);
p = NULL;
}
// 时间复杂度:O(m)
// 空间复杂度: O(n)
9. 两种思想混合-----双指针与反转

算法设计:
- 通过快慢指针法 找到 中间节点
- 将后半段原地逆置
- 交叉连接结点
void rearrange(LinkList l)
{
// 寻找链表中间结点
Node* slow = l;
Node* fast = l;
while (fast->next != NULL)
{
slow = slow->next;
fast = fast->next;
if (fast->next != NULL)
{
fast = fast->next;
}
}
// second 为后半段链表 首元结点
Node* second = slow->next;
// 分割链表
slow->next = NULL;
// 后半段指针逆置
Node* temp = NULL;
Node* prev = NULL;
Node* curr = second;
while (curr != NULL)
{
temp = curr->next;
curr->next = prev;
prev = curr;
curr = temp;
}
// curr 为NULL,prev 指向反转后的首元节点
// 合并两个链表
Node* p = l->next;
Node* q = prev;
Node* next_p;
Node* next_q;
while (p != NULL && q != NULL)
{
next_p = p->next;
next_q = q->next;
p->next = q;
q->next = next_p;
p = next_p;
q = next_q;
}
}
// 时间复杂度 O(n)
四. 总结
常用的算法设计技巧,仅供参考:头插法、尾插法、反转、归并、快慢指针




















 5万+
5万+










