深度学习中常见的优化器小结

优化器的挑战

局部最优
如以下函数$f(x)=cos(\pi x)$

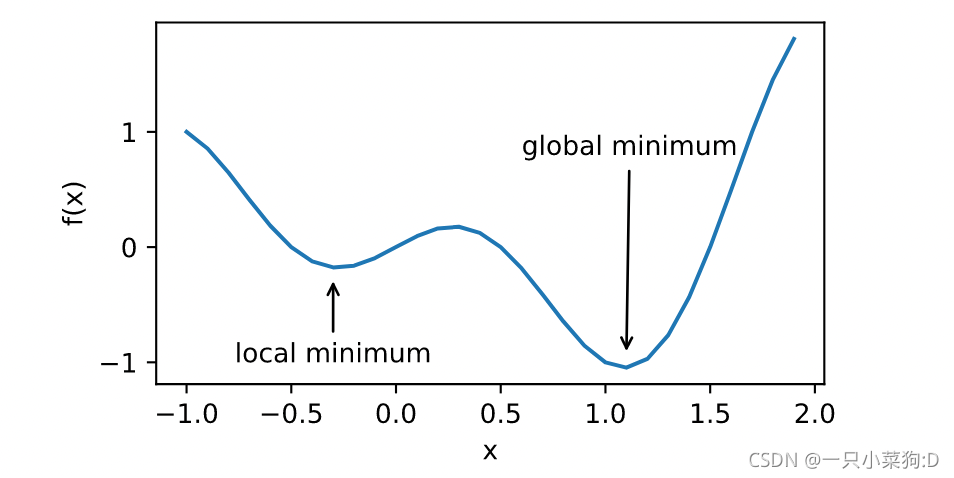
当一个优化问题的数值解在局部最优解附近时，由于目标函数有关解的梯度接近或变成零，最终迭代求得的数值解可能只令目标函数局部最小化而非全局最小化。
鞍点
梯度接近0可能是在局部最优解，但也有可能在鞍点附近。比如：

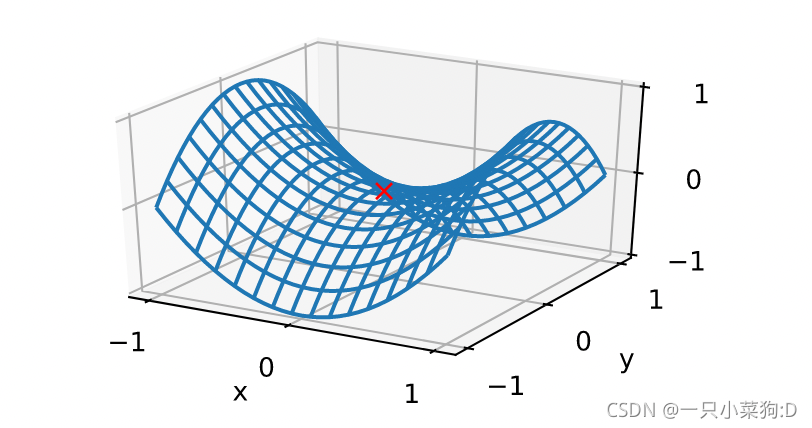
与局部最小不同，如果我们能往“正确”的方向前进一步，那么有可能逃离鞍点。幸运的是，我们有方法去判断这个点是局部最优还是在鞍点。
$$J(\theta )=J({\theta }_0)+(\theta -{\theta }_0){\nabla }_{\theta }J({\theta }_0)+\frac{1}{2}(\theta -{\theta }_0)H(\theta -{\theta }_0{)}^T$$
其中，H是海瑟矩阵。因为我们现在卡在了梯度为0的点，因此，该式子可以转化为：
$$J(\theta )=J({\theta }_0)+\frac{1}{2}(\theta -{\theta }_0)H(\theta -{\theta }_0{)}^T$$
那么，不难得出，如果对于所有的$\theta$,都有：
$\frac{1}{2}(\theta -{\theta }_0)H(\theta -{\theta }_{}$