备战数学建模十三之BP神经网络

原创已于 2022-08-06 13:04:58 修改 · 454 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#神经网络 #python #机器学习

于 2022-08-06 09:52:46 首次发布

两段代码展示了BP神经网络的实现，分别处理逻辑运算和加或逻辑问题。第一段代码定义了激活函数、前向传播、反向传播和权重更新，并通过迭代优化权重。第二段代码为一个简单的两层神经网络，用于解决与或逻辑问题，通过sigmoid函数和梯度下降法更新权重，随着训练次数增加，损失函数逐渐减小。

话不多说，直接上代码，反正都不是自己的东西，稍微改了改，让代码能用了

# encoding:utf-8
# ********* 导入相应的模块***********
import math
import numpy as np
from numpy import *

#**********设定模型所需的激活函数，运行此代码时，带'*'部分请删除*********
# 激活函数
def sigmoids(z):
    #Sigmoid函数是一个在生物学中常见的S型函数，也称为S型生长曲线。1/(1+e^(-x))
    # Sigmoid函数常被用作神经网络的激活函数，将变量映射到0,1之间。
    a = []
    for each in z:
        b = 1/(1+math.exp(-each[0]))
        a.append(b)
    return a

# **********设定前向传播过程，即模型的设定部分，此处均根据模型第3部分的模型设定部分的公式编写对应的代码*********

# 前向传播,返回预测值
def forwordmd(X,W,V,B1,B2):
    net1 = W.T*X+B1
    H = matrix(sigmoids(np.array(net1))).T # 隐藏层单元
    net2 = V.T*H+B2
    pred_y = matrix(sigmoids(np.array(net2))).T # 预测值
    return pred_y,H,net1,net2

#**********设定模型反向传播，按照步骤4的公式编辑*********
# 反向传播,更新权重
def Bpaugorith(Y,pred_y,H,V,aph,W):
    Errorterm = 0.5*(Y-pred_y).T*(Y-pred_y)# 给出误差公式
    # 计算输出单元的误差项
    a1 = multiply(pred_y-Y,pred_y) # 矩阵对应元素相乘,即逐元素相乘
    a2 = multiply(a1,1-pred_y)
    Verror = H*a2.T
    # 计算隐藏单元的误差项
    Werror = X*(multiply(multiply(H,1-H),(V*a2))).T
    # 更新权重
    Vupdate = V - aph*Verror
    Wupdate = W - aph*Werror
    return Vupdate,Wupdate,Errorterm

#**********主程序部分，此处设定了步骤1中的参数初始化和输入值及输出值的真实值，及步骤5中设置迭代次数和设置阈值停止迭代的代码*********

if __name__ =='__main__':
    X = matrix([0.05,0.10]).T#训练数据
    Y = matrix([0.01,0.99]).T
    # # 给出初始权重
    # W = matrix([[0.15,0.20],[0.25,0.30]])
    # B1 = matrix([0.1,0.1]).T
    # V = matrix([[0.40,0.45],[0.50,0.55]])
    # B2 = matrix([0.2,0.2]).T

    # ***********初始权重亦可随机生成***********
    # 随机生成参数
    np.random.seed(0)
    W = matrix(np.random.normal(0,1,[2,2]))
    B1 = matrix(np.random.normal(0, 1, [1, 2]))
    V = matrix(np.random.normal(0, 1, [2, 2]))
    B2 = matrix(np.random.normal(0, 1, [1, 2]))
    # ***********随机生成参数部分，若有自己设定，将此部分注释*********
    aph = 0.1 # 学习率,梯度下降法的步长，太小容易局部最小值，太大误差大跳过最优解
    #*********从此处为迭代次数设置部分***********
    # 迭代10次
    n = 100000 # 迭代次数
    for i in range(n):
        # 激活前向算法
        pred_y, H,net1,net2 = forwordmd(X,W,V,B1,B2)  # 得到预测值和隐藏层值
        # 更新权重
        Vupdate, Wupdate,Errorvalue = Bpaugorith(Y,pred_y,H,V,aph,W)  # 得到更新的权重
        W,V = Wupdate,Vupdate

    X2=matrix([0.6,0.8]).T
    y,a,b,c=forwordmd(X2,W,V,B1,B2)
    print("预测值2",y)
    print ('损失函数e：%.2f'%e)
    print ('预测值：')
    print (pred_y)
    print ('更新的权重V：')
    print (Vupdate)
    print ('更新的权重W:')
    print (Wupdate)
    print ('损失值：')
    print (Errorvalue)

    # 阈值E，可根据需要自行更改，若需要运行此部分，请将迭代次数部分注释后运行
    # 阈值E
    # e,m = 0.19,1
    # pred_y, H, net1, net2 = forwordmd(X,W,V,B1,B2)  # 得到预测值和隐藏层值
    # 更新权重
    # Vupdate, Wupdate, Errorvalue = Bpaugorith(Y,pred_y,H,V,net1,net2,aph,W)  # 得到更新的权重
    # W,V = Wupdate,Vupdate
    # while Errorvalue>e:
        # 激活前向算法
        # pred_y, H, net1, net2 = forwordmd(X,W,V,B1,B2)  # 得到预测值和隐藏层值
        # 更新权重
        # Vupdate, Wupdate, Errorvalue = Bpaugorith(Y,pred_y,H,V,net1,net2,aph,W)  # 得到更新的权重
        # W, V = Wupdate, Vupdate
        # m = m+1
    # print ('迭代次数：%d'%n)
    # print ('更新权重:%d次'% m)
    # print ('预测值：')
    # print (pred_y)
    # print ('更新的权重V：')
    # print (Vupdate)
    # print ('更新的权重W:')
    # print (Wupdate)
    # print ('损失值：')
    # print (Errorvalue)
# 
#
#     #*********阈值设置部分结束***********
#
#

运行结果

预测值2 [[0.0068899 ]
 [0.99291294]]
损失函数e：2.72
预测值：
[[0.01094523]
 [0.98905563]]
更新的权重V：
[[-2.07238957  2.15949174]
 [-3.14612034  2.73716063]]
更新的权重W:
[[1.78677904 0.4463306 ]
 [1.02419138 2.33323999]]
损失值：
[[8.92654732e-07]]

进程已结束,退出代码0

在加一个与或逻辑的BP神经网络的代码

import numpy as np
import matplotlib.pyplot as plt
# 输入数据，输入二维，中间十个神经元，输出是一维
X = np.array([[0,0],[0,1], [1,0],[1,1]])
# 标签，也就是输出值的实际值，这个例子仿佛是与或非之类的东西
T = np.array([[0],[1],[1],[0]])
# 定义一个2层的神经网络：2-10-1
# 输入层2个神经元，隐藏层10个神经元，输出层1个神经元
# 输入层到隐藏层的权值初始化，2行10列
W1 = np.random.random([2,10])
# 隐藏层到输出层的权值初始化，10行1列
W2 = np.random.random([10,1])
# 初始化偏置值，偏置值的初始化一般可以取0，或者一个比较小的常数，如0.1
# 隐藏层的10个神经元偏置
b1 = np.zeros([10])
# 输出层的1个神经元偏置
b2 = np.zeros([1])
# 学习率设置
lr = 0.1
# 定义训练周期数
epochs = 100001
# 定义测试周期数
test = 5000
# 定义sigmoid函数
def sigmoid(x):
 return 1/(1+np.exp(-x))
# 定义sigmoid函数导数
def dsigmoid(x):
 return x*(1-x)
# 更新权值和偏置值
def update():
 global X,T,W1,W2,lr,b1,b2
 # 隐藏层输出
 L1 = sigmoid(np.dot(X,W1) + b1)
 # 输出层输出
 L2 = sigmoid(np.dot(L1,W2) + b2)
 # 根据公式4.41，求输出层的学习信号
 delta_L2 = (T - L2) *dsigmoid(L2)
 # 根据公式4.42，求隐藏层的学习信号
 delta_L1 = delta_L2.dot(W2.T) *dsigmoid(L1)
 # 根据公式4.44，求隐藏层到输出层的权值改变
 # 由于一次计算了多个样本，所以需要求平均
 delta_W2 =lr*L1.T.dot(delta_L2) /X.shape[0]
# 根据公式4.45，求输入层到隐藏层的权值改变
# 由于一次计算了多个样本，所以需要求平均
 delta_W1 =lr*X.T.dot(delta_L1) / X.shape[0]
 # 更新权值
 W2 =W2 + delta_W2
 W1 =W1 + delta_W1
 # 改变偏置值
 # 由于一次计算了多个样本，所以需要求平均
 b2 =b2 +lr*np.mean(delta_L2, axis=0)
 b1 =b1 +lr*np.mean(delta_L1, axis=0)
# 定义空list用于保存loss
loss = []
# 训练模型
for i in range(epochs):
 # 更新权值
    update()
 # 每训练5000次计算一次loss值
    if i %test == 0:
 # 隐藏层输出
       L1 = sigmoid(np.dot(X,W1) + b1)
 # 输出层输出
       L2 =sigmoid(np.dot(L1,W2) + b2)
 # 计算loss值
       print('epochs:',i,'loss:',np.mean(np.square(T - L2) / 2))
 # 保存loss值
       loss.append(np.mean(np.square(T - L2) / 2))
# 画图训练周期数与loss的关系图
plt.plot(range(0,epochs,test),loss)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
# 隐藏层输出
L1 = sigmoid(np.dot(X,W1) + b1)
# 输出层输出
L2 = sigmoid(np.dot(L1,W2) + b2)
print('output:')
print(L2)
# 因为最终的分类只有0和1，所以我们可以把
# 大于等于0.5的值归为1类，小于0.5的值归为0类
def predict(x):
 if x>=0.5:
  return 1
 else:
  return 0
# map会根据提供的函数对指定序列做映射
# 相当于依次把L2中的值放到predict函数中计算
# 然后打印出结果
print ('predict:')
for  i in map(predict,L2):
 print(i)

输出结果为

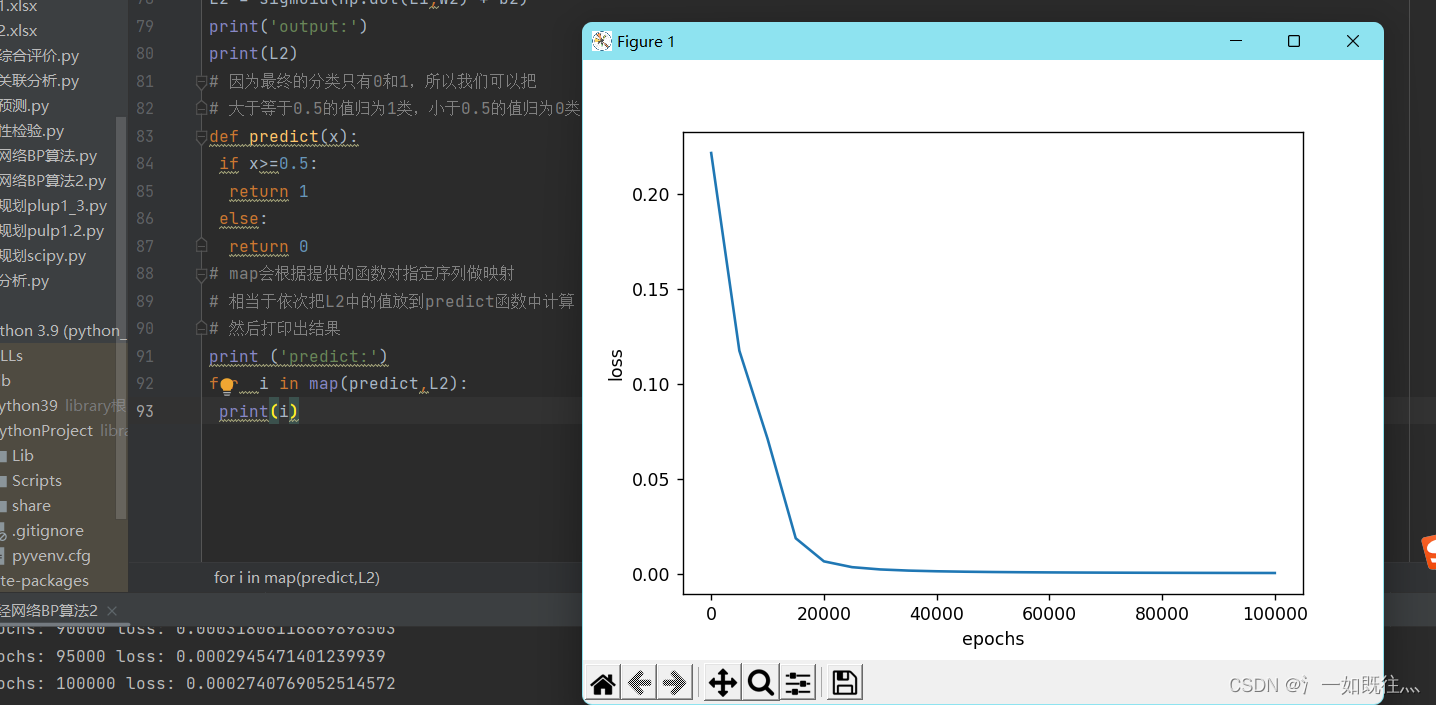
epochs: 0 loss: 0.22163212148744935
epochs: 5000 loss: 0.11741534349499161
epochs: 10000 loss: 0.07103471018518064
epochs: 15000 loss: 0.01857399836442719
epochs: 20000 loss: 0.006409280131915647
epochs: 25000 loss: 0.0033496302930681445
epochs: 30000 loss: 0.002149399523007848
epochs: 35000 loss: 0.0015422805098843926
epochs: 40000 loss: 0.0011852096578871705
epochs: 45000 loss: 0.0009535961890505724
epochs: 50000 loss: 0.00079275000040673
epochs: 55000 loss: 0.0006753101872422451
epochs: 60000 loss: 0.0005862188584680112
epochs: 65000 loss: 0.0005165657747824863
epochs: 70000 loss: 0.00046076940594204114
epochs: 75000 loss: 0.00041516911394270175
epochs: 80000 loss: 0.00037727163060337517
epochs: 85000 loss: 0.00034532421602544156
epochs: 90000 loss: 0.00031806116869898503
epochs: 95000 loss: 0.0002945471401239939
epochs: 100000 loss: 0.0002740769052514572
Can't find filter element
Can't find filter element
output:
[[0.02483329]
 [0.97753863]
 [0.97770082]
 [0.02396155]]
predict:
0
1
1
0

进程已结束,退出代码0