【原创】《矩阵的史诗级玩法》连载二十八：二次贝塞尔曲线和椭圆的矩阵求交计算

这次的拖延，除了拖延症发作，还有一个原因是我最近在做项目中发现圆弧在图形软件中并不好用，椭圆弧就更不用说了。

虽然圆弧在解方程方面比贝塞尔曲线简单很多，但是有一个很大的弊端。这个弊端我写了好多遍草稿，但总感觉还是大多数人看不明白，因为我觉得没有在实战中踩过那些坑都很难理解，而且浮点误差的问题在很多人眼里都是小事，我怎么解释都很难让大家认清这一问题的严重性。

总的来说，我觉得圆弧还不如贝塞尔曲线实用性强。所以有很长一段时间我在纠结要不要把二次贝塞尔曲线以外的其它二次曲线给写到这里来。

当然了，最后我还是选择继续写，理论的东西，写完整点还是有好处的。

前面说过，椭圆可以用一个标准圆（单位圆）+一个变换矩阵来表达。到几何层面，这个变换会被细化为长短轴，圆心，长轴向量等属性。

 

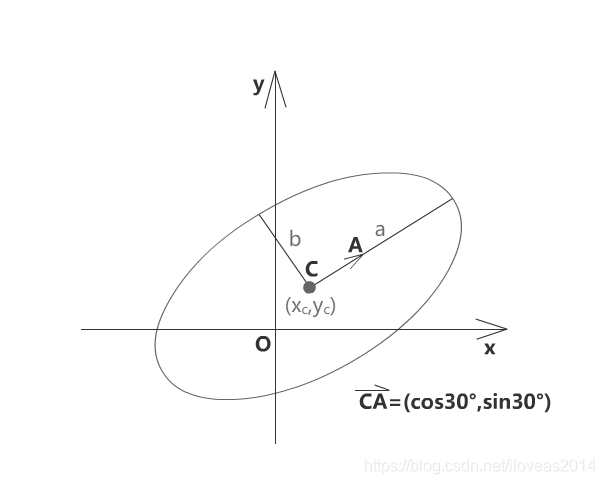
在CAD中，长轴向量没有单位化，直接用a的长度来表示，然后加一个长短轴的比例来获得短轴的长度。当然了，这些都只是形式上的差异，最终结果殊途同归。

现在我们以单位圆x^2+y^2=1为基准，把这些属性组合成一个矩阵。从单位圆变化到上图的斜椭圆，可以分解成以下几个步骤。

1 横向缩放a，纵向缩放b

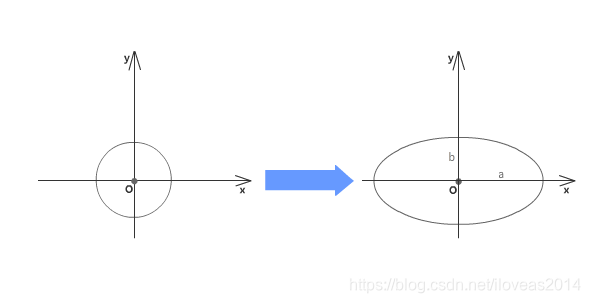
2 逆时针旋转30度

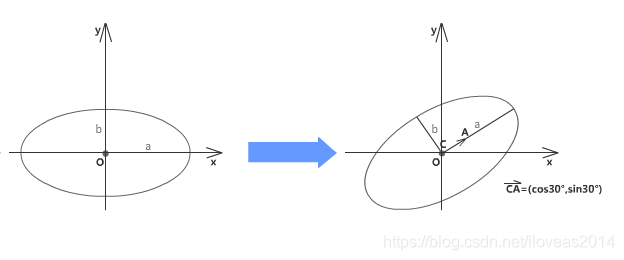
3 平移（xc,yc）

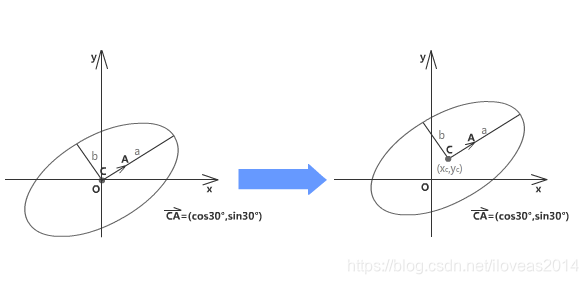
这里就不啰嗦了，直接给出三个变换连乘的矩阵。

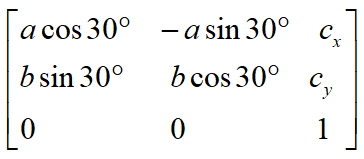
这个矩阵乘以变换前的点（x, y）得到变换后的点（X, Y）

所以按照前面的套路，把以上矩阵的逆矩阵放入到单位圆方程x^2+y^2=1即可。

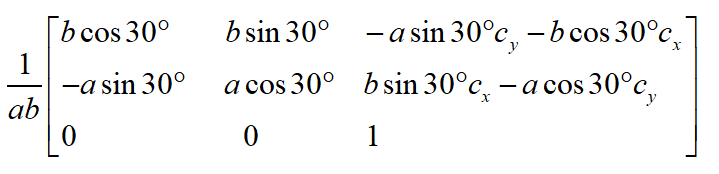
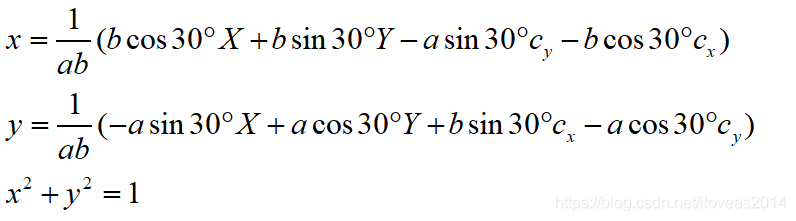
得到

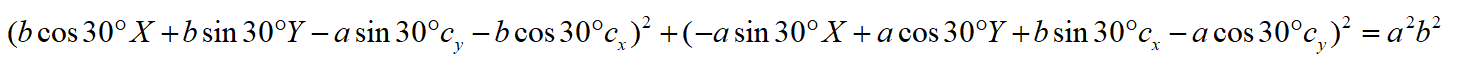
这个式子看着蛮复杂的，所以如果知道变换的具体参数，那是不会考虑直接拿这个方程来求解的。

现在我们可以开始探讨贝塞尔曲线如何跟椭圆求交了。

按照矩阵法的套路，做法是把其中一条曲线通过矩阵转换为标准曲线，然后对另一条曲线应用同一个矩阵。

我们知道，二次贝塞尔曲线的变换可以转化为3个关键点的变换，但是椭圆看起来就麻烦了，因为以二次贝塞尔曲线为基准的话，我们就得在椭圆方程的基础上继续叠加矩阵，式子会变得更加蛋疼。

因此，我们先把椭圆变成单位圆，用的是上面给出的逆矩阵。结果不用算，就是x^2+y^2=1

而贝塞尔曲线就没什么好说的了，直接对3个点应用逆矩阵，生成新的方程即可。新方程仍为贝塞尔曲线，因此形式可以这样表示。

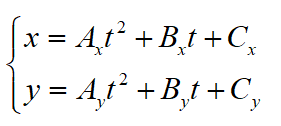
再跟单位圆方程联立，即可得到一个一元四次方程，交点可由此求得。

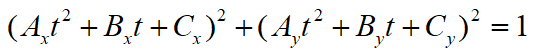
看起来好像很简单，但这个地方跳跃有点大。嗯，那些系数其实是需要经过几步运算出来的。

已知贝塞尔曲线的3个点为(x0,y0),(x1,y1),(x2,y2)，中间的是控制点，那么我们先算出这3个点在经过椭圆逆矩阵变换后的结果，得到

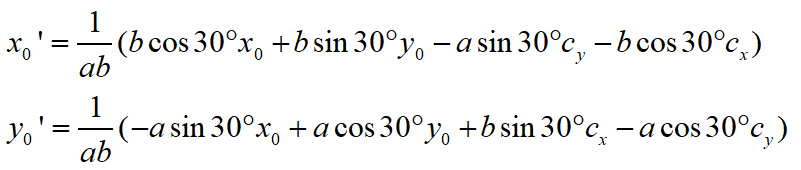
另外两个点的计算方法类似，不再重复。

接着利用连载十七给出的系数和点的关系式

求得

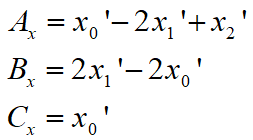
y的也类似，也不重复了。

在这个演算过程中，式子最繁琐的莫过于矩阵变换点那个地方了，然而在代码里我们已经把这个算法封装到矩阵里，所以这个求交过程会相当简洁，下篇我就把代码给出来！大家先喝口水休息一下~